
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. Интегрирование степенных функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Наиболее распространенным является интеграл от степенной функции (таблица интегралов, с. 33). Для вычисления этих интегралов необходимо знать следующие правила действий со степенями, приведенными на стр. 26. Пример 1 Вычислить:
Задание 1 к разделу 1
II. Интегрирование заменой переменной Этот метод интегрирования основан на введении в подынтегральную функцию новой переменной величины и ее дифференциала, причем замену переменной необходимо подбирать таким образом, чтобы в исходном интеграле присутствовал дифференциал новой переменной в явном виде. Рассмотрим несколько примеров. Пример 2 Вычислить:
Пример 3 Вычислить:
Пример 4 Вычислить:
Замечание: после введения новой переменной и вычисления интеграла необходимо вернуться к исходной переменной.
Задание 2 к разделу 1 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. III. Интегрирование по частям Формула интегрирования по частям имеет вид В этом случае степенная функция
Пример 5 Вычислить:
Кроме указанных интегралов по этой же формуле вычисляются интегралы вида: Пример 6 Вычислить:
Пример 7 Вычислить:
Задание 3 к разделу 1
IV. Интегрирование рациональных дробей Рассмотрим интегрирование рациональных дробей вида:
где Если Интегрируются только правильные дроби, поэтому, если под интегралом дробь неправильная, то ее необходимо представить в виде суммы целой части и правильной дроби, а затем выполнять интегрирование.
Пример 8 Вычислить:
Рассмотрим теперь интегрирование правильной дроби. Для этого ее надо представить в виде суммы простейших дробей и привести к общему знаменателю:
где А и В – неопределенные коэффициенты, так как
Таким образом, правильная дробь представляется суммой двух простейших дробей:
Выполним теперь интегрирование исходного интеграла:
Рассмотрим интегрирование квадратного трехчлена путем выделения полного квадрата и приведения исходного интеграла к табличному.
Пример 9 Вычислить:
Пример 10 Вычислить:
Пример 11 Вычислить:
Теоретические вопросы к разделу 1 1. Неопределенный интеграл, его свойства. 2. Интегрирование заменой переменной. 3. Формула интегрирования по частям, типы интегралов, которые вычисляются по этой формуле. Задание 4 к разделу 1
Раздел 2. Определенный интеграл Определенный интеграл с постоянными пределами интегрирования имеет вид:
где а – нижний предел интегрирования; b – верхний предел интегрирования; Вычисляется определенный интеграл по формуле Ньютона–Лейбница:
т. е. для вычисления необходимо найти первообразную
Пример 1 Вычислить:
При вычислении определенного интеграла заменой переменных необходимо вводить новые пределы интегрирования, соответствующие новой переменной.
Пример 2 Вычислить:
Вычисление определенного интеграла по частям.
Пример 3 Вычислить:
Теоретические вопросы к разделу 2 1. Определенный интеграл, его свойства. Формула Ньютона–Лейбница. 2. Интегрирование определенного интеграла заменой переменной и по частям. Задание 1 к разделу 2 Вычислить:
Раздел 3. Вычисление площади плоской фигуры Последовательность вычисления площади плоской фигуры, с помощью определенного интеграла следующая (рис. 4): 1) находим точки пересечения заданных линий; 2) находим точки пересечения линий с координатными осями; 3) строим область, ограниченную линиями на плоскости XОУ; 4) составим определенный интеграл и вычислим искомую площадь.
Пример 1 Найти площадь, ограниченную линиями Решение: Находим точки пересечения линий. Для этого приравняем правые части уравнений:
т. е. точки пересечения
Строим заданные линии на плоскости ХОУ: 1) точки пересечения параболы:
2) через точки А и В проводим прямую. Через точки 3) составляем определенный интеграл:
где
Рис. 4
В нашем случае:
Теоретические вопросы к разделу 2 1. Схема вычисления площади плоской фигуры определенным интегралом, нахождение пределов интегрирования, построение подынтегральной функции.
Задание 1 к разделу 3 Вычислить площадь, ограниченную линиями:
Список рекомендованной литературы 1. Беклемишев, Д.В. Курс аналитической геометрии и линейной алгебры: учеб. для вузов / Д.В. Беклемишев. – М.: Физматлит, 2006. – 312 с. 2. Боревич, З.И. Определители и матрицы: учеб. пособие / З.И. Боревич. – СПб.: Лань, 2004. – 192 с. 3. Привалов, И.И. Аналитическая геометрия: учебник / И.И. Привалов. – СПб.: Лань, 2004. – 304 с. 4. Пискунов, Н.С. Дифференциальное и интегральное исчисление для втузов: учеб. пособие для втузов. В 2 т. Т. 1 / Н.С. Пискунов. – М.: Интеграл-Пресс, 2006. – 416 с. 5. Пискунов, Н.С. Дифференциальное и интегральное исчисление: учеб. пособие для втузов. В 2 т. Т. 2 / Н.С. Пискунов. – М.: Интеграл-Пресс, 2005. – 544 с. 6. Данко, П.Е. Высшая математика в упражнениях и задачах: учеб. 7. Данко, П.Е. Высшая математика в упражнениях и задачах: учеб. 8. Шипачев, В.С. Высшая математика: учеб. пособие для втузов / В.С. Шипачев. – М.: Высш. шк., 2006. – 479 с. ОГЛАВЛЕНИЕ ВВЕДЕНИЕ............................................................................................................ 3 Контрольная работа № 1. Элементы линейной Раздел 1. Системы «n» линейных алгебраических уравнений Раздел 2. Элементы векторной алгебры и аналитической геометрии 9 Раздел 3. Базис. Разложение вектора по базисным векторам.......... 12 Контрольная работа № 2. комплексные числа, пределы, исследование непрерывности функции....................................................................... 13 Раздел 1. Комплексные числа................................................................... 13 Раздел 2. Пределы...................................................................................... 17 Раздел 3. Исследование непрерывности функции Контрольная работа № 3. Производные и элементы исследования функций............................................................................................................ 25 Раздел 1. Производные.............................................................................. 25 Раздел 2. Экстремум функции, его классификация.............................. 29 Раздел 3. Наибольшее и наименьшее значение функции Контрольная работа № 4. Неопределённый Раздел 1. Неопределенный интеграл...................................................... 33 Раздел 2. Определенный интеграл.......................................................... 42 Раздел 3. Вычисление площади плоской фигуры................................. 45 Список рекомендованной литературы......................................... 48
Учебное издание
Константинов Никита Сергеевич Смотрова Марьяна Сергеевна Богомякова Татьяна Анатольевна
ВЫСШАЯ МАТЕМАТИКА
Методическое пособие по выполнению
|
|||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 994; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.214.139 (0.009 с.) |

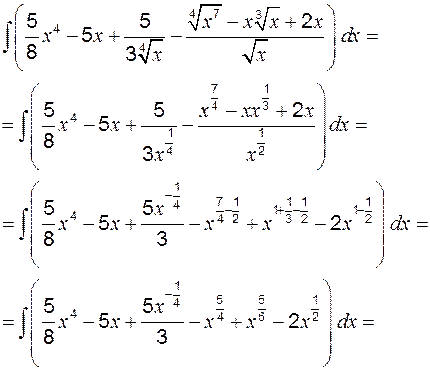
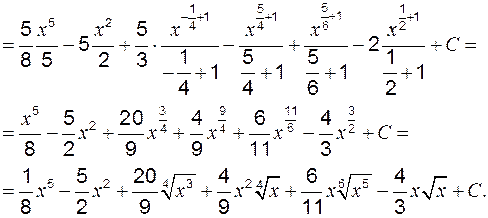
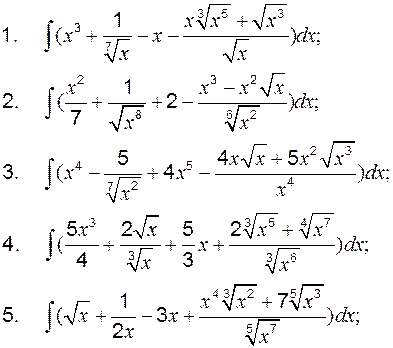
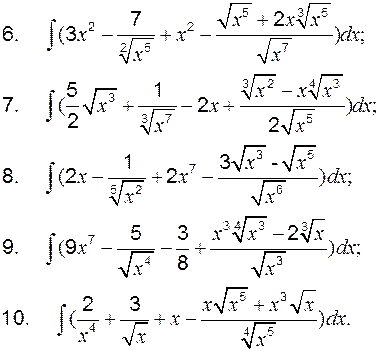
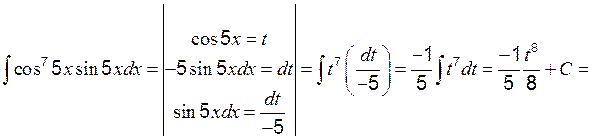
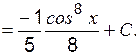
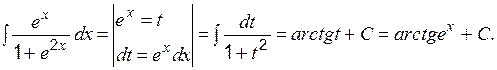
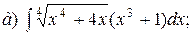
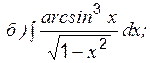
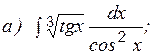
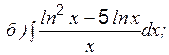
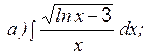
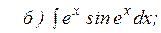
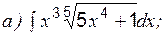
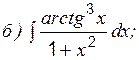
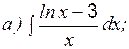
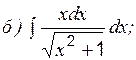
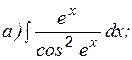
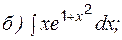
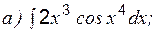
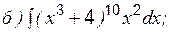
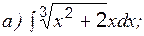
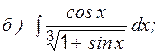
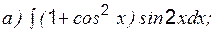
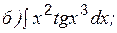
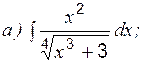
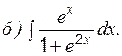
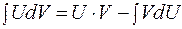 ,
,  необходимо, вводя новые функции
необходимо, вводя новые функции 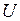 и
и 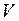 , представить в виде
, представить в виде 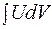 , а затем построить правую часть формулы. По такой формуле вычисляются интегралы вида:
, а затем построить правую часть формулы. По такой формуле вычисляются интегралы вида: 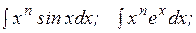
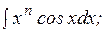 причем, вместо
причем, вместо 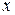 может быть линейная подстановка
может быть линейная подстановка 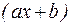 .
.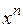 обозначается функцией
обозначается функцией 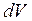 – все остальные множители. Формулу интегрирования по частям можно применять многократно, например, в вышеуказанных интегралах формулу необходимо применить «
– все остальные множители. Формулу интегрирования по частям можно применять многократно, например, в вышеуказанных интегралах формулу необходимо применить «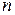 » раз.
» раз.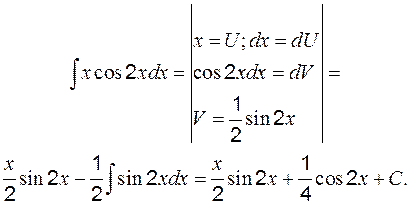
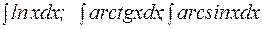 и т.п.
и т.п.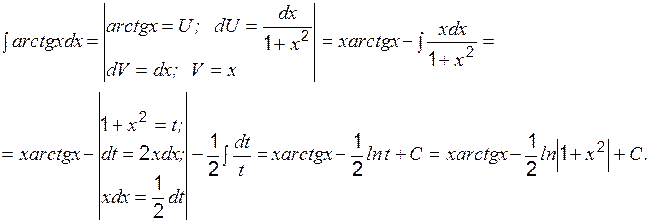
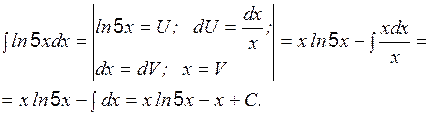
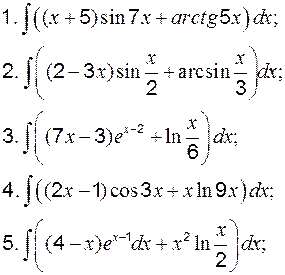
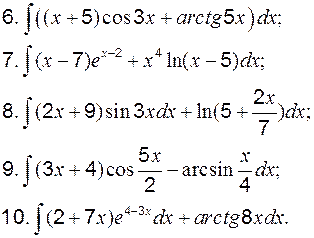
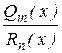 ,
,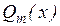 и
и 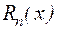 – рациональные многочлены степени
– рациональные многочлены степени  и
и 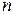 .
.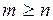 , то дробь называется неправильной, если
, то дробь называется неправильной, если 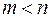 , то дробь – правильная.
, то дробь – правильная.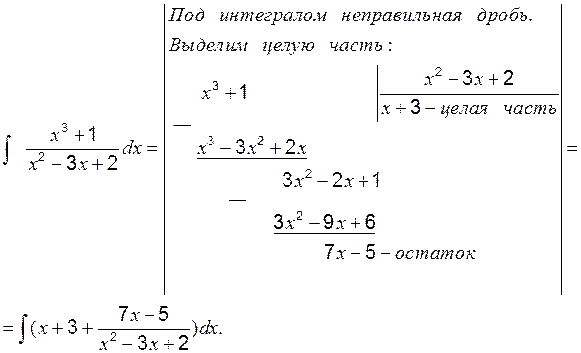

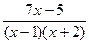 =
= 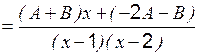 , то
, то 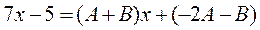 , приравнивая коэффициенты при
, приравнивая коэффициенты при 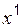 и при
и при 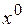 , получаем систему:
, получаем систему: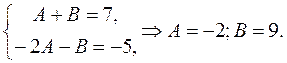
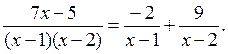

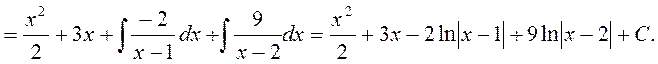
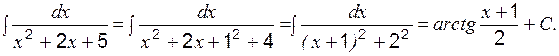
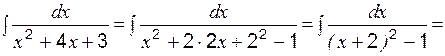
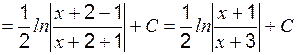 .
.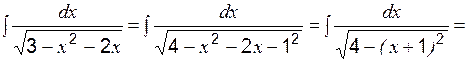
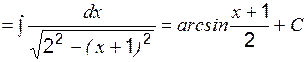 .
.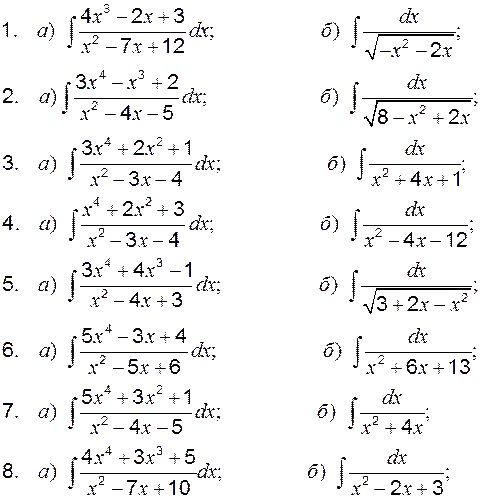
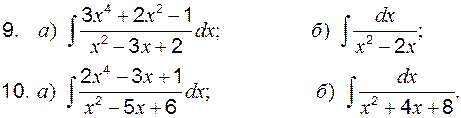
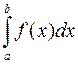 ,
,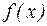 – подынтегральная функция.
– подынтегральная функция.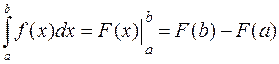 ,
,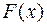 , подставив вместо
, подставив вместо 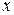 верхний предел
верхний предел 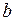 и вычесть значение первообразной при
и вычесть значение первообразной при  .
.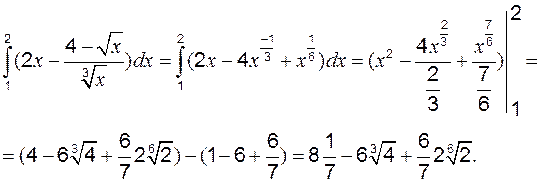
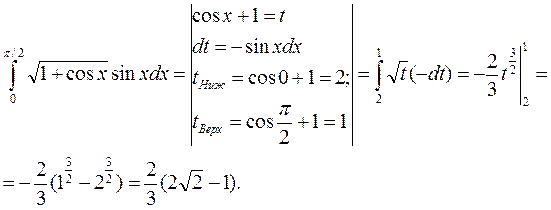
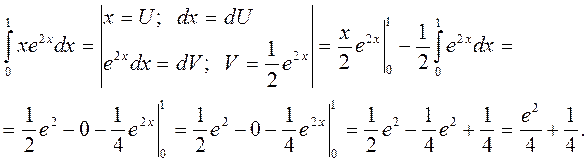
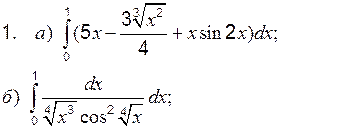

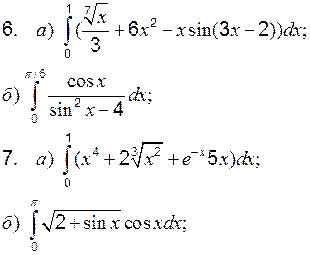
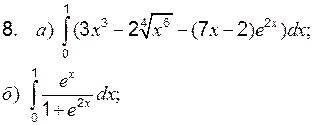
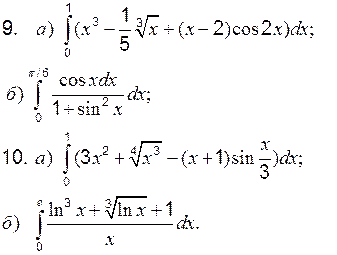
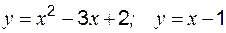 .
.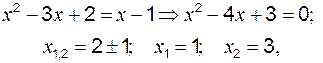
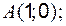
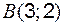 (рис. 4).
(рис. 4).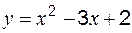 с осью ОХ:
с осью ОХ: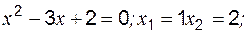
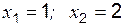 на оси ОХ и точки А и В проводим параболу. Получаем область, ограниченную линиями, площадь которой необходимо вычислить;
на оси ОХ и точки А и В проводим параболу. Получаем область, ограниченную линиями, площадь которой необходимо вычислить;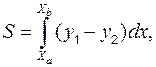
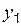 – линия, ограничивающая область сверху;
– линия, ограничивающая область сверху; 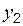 – линия, ограничивающая область снизу;
– линия, ограничивающая область снизу;  – наименьшее значение переменной
– наименьшее значение переменной 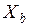 – наибольшее значение переменной
– наибольшее значение переменной 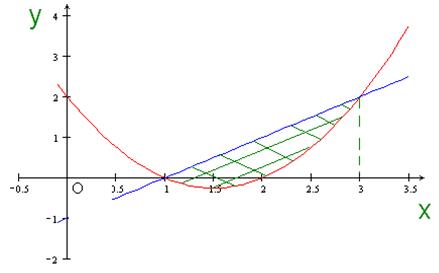
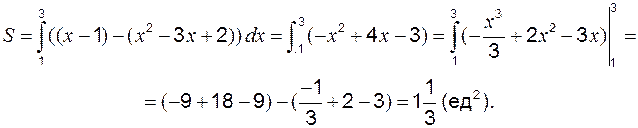
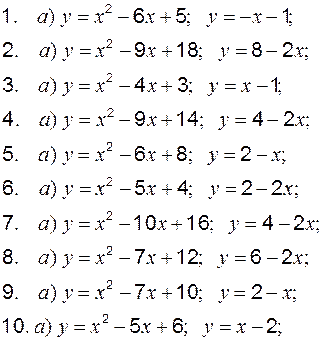
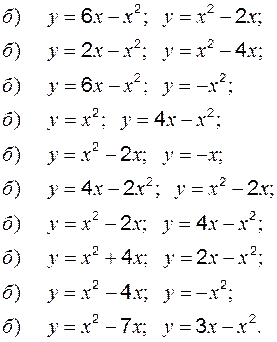
 » и «
» и «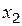 »................................................................. 22
»................................................................. 22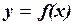
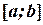 ............................................................................................ 31
............................................................................................ 31



