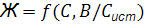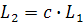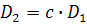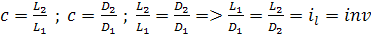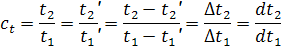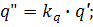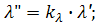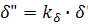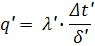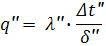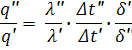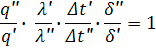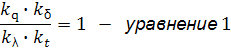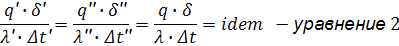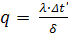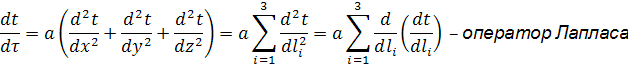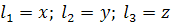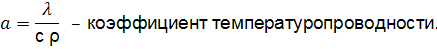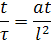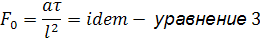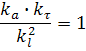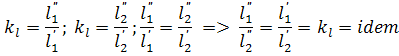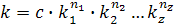Классификация моделей по В. А. Вознесенкому

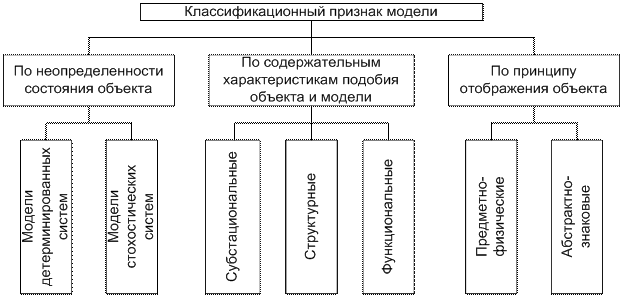
Классифицировать модели можно различными способами, которые определяются постановкой задачи. Применительно к технологии строительных материалов профессор В.А. Вознесенский предлагает классифицировать модели по признакам:

    схема классификации

К модели детерминированных систем, относят такие, в которых все элементы взаимодействуют точно предвиденным способом, а случайные факторы ξ практически не влияют на течение процесса. В отличие от них модели стохастических систем подчиняются вероятностным законам. На поведение отдельных элементов таких моделей существенно влияют случайные входы.

Субстанциональные модели строят таким образом, чтобы их материал по своим свойствам был подобен материалу объекта. Например, для определения фактической прочности бетона в эксплуатируемой конструкции из нее выпиливают образец, который затем испытывают на прочность.

Структурные модели имитируют структуру или способ взаимодействия элементов объекта между собой. В промышленности строй материалов такие модели обычно строят для выявления оптимальных транспортных связей, например между ДСК (домостроительный комбинат) и строками, ДСК и поставщиками сырья.

Функциональные модели имитируют одну или несколько основных (определяющих функций объекта), например: известно что жесткость бетонной смеси является функцией концентрации С цементного теста в бетоне и истинного водоцементного отношения В/С_ист.

Выявив опытным путем, вид функции f получают функциональную модель жесткости бетонной смеси.

К предметно-физическим относятся модели сохраняющие в основном природу явления. Примером может служить определение прочности бетона в конструкции выпиливанием из нее образцов являющихся одновременно и субстанциональными моделями.

Абстрактно-знаковые модели отражают взаимосвязь элементов системы с помощью дифференциальных или алгебраических уравнений, геометрических соотношений, логических операций и т.п. Частным случаем таких моделей являются математические модели широко применяемые в настоящее время. На сегодняшний день нет единой общепринятой классификации математических моделей. В различных областях их применения вводятся различные классификационные признаки.

9.3. Подобные явления. Константы и инварианты подобия, индикаторы подобия, симплексы (параметрические критерии), критерии подобия (определяющие и не определяющие), теоремы подобия, критериальные уравнения.

Теория подобия - наука о подобных явлениях.

Подобными явлениями называются системы тел, геометрически подобные друг другу, в которых протекают процессы одинаковой физической природы, и в которых одноименные причины, характеризующие явления, относящиеся между собой как постоянные числа.

Принцип выделения группы подобных явлений из класса однородных можно уяснить на следующем простом примере:

Из класса однородных аппаратов, допустим, барабанных сушилок выделяют группу подобных аппаратов отличающихся только масштабами. Если аппарат и его модель геометрически подобны, то:

где индекс 2 относится к промышленному аппарату, а 1 - к модели.

Для одной пары автоматов величина масштабного множителя С является константой геометрического подобия.

Подобия этой пары аппаратов можно выразить и другим способом по средствам инвариантов подобия.

Для рассматириваемого примера геометрического подобия можно записать:

 

где i_l - инвариант геометрического подобия представляющий собой безмерное отношение двух размеров малого барабана L₁ к D₁ (модели) равно отношению сходственных размеров подобного ему производственного барабана.

Инварианты подобия представляют собой выражение величины в относительных единицах. В примере один размер (длина) подобных аппаратов выражена в относительных единицах. В качестве масштаба применяют их другой пример (диаметр).

Отличие константы подобия от инварианта в том, что константа сохраняет постоянное значение во всех точках системы, но она изменяется, когда одна пара подобных явлений заменяется другой парой той же группы.

инвариант подобия наоборот различен для разных точек системы, но он не меняется при переходе от одного явления к любому другому, подобному ему, т.е. сохраняет одно и то же значение в сходственных точках всех групп подобных явлений.

Отметим еще одно свойство констант подобия: входящие в них одноименные величины могут взаимозаменяться, т.е. отношение самих величин можно заменять отношением приращений этих величин:

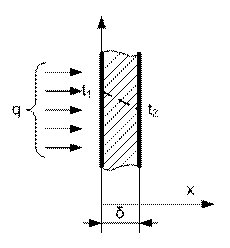
При рассмотрении сложных процессов, которые определяются многими физическими величинами выбирать произвольно константы подобия этих величин нельзя. Для этих процессов, при выборе констант подобья имеются ограничения, которые находят, исследуя уравнения описывающие процесс.

Рассмотрим правило выбора констант подобия на конкретном примере уравнений теплопроводности для плоской однородной стенки при стационарном процессе (рис ниже).

Теплопередача через однородную плоскую стенку.

На основании закона Фурье плотность теплового потока известна и будет равна:

где q - плотность теплового потока; λ - теплопроводность материала стенки, δ - ее толщина, t1 и t2 - постоянные температуры на поверхности стенки.

Пусть первая - основная - система характеризуется значениями параметров q', λ', δ', а вторая:

Значения параметров второй системы получены путем уменьшения значения параметров первой системы на соответствующие константы подобия. Тогда для первой системы имеем:

а для второй:

 разделив одно на другое получим:

Подставляя вместо отношения величин их константы подобия:

Функции типа уравнения 1 связывающие константы подобия называются индикаторами подобия - j.

Из уровнения 1 следует весьма важный вывод: При выборе числовых значений констант подобия для группы подобных явлений необходимо соблюдение условия (j=1). Т.е. выбор значений констант условия не произволен. Требования к выбору констант подобий обусловленные уравнение 1 для рассматриваемого примера можно представить в другом, более удобном виде.

Если в указанном уравнении константу подобия представить как отношение соответствующих параметров и все уравнения с одним штрихом сгруппировать в левой части, а с двумя в правой, то:

Уравнение 2 демонстрирует основное свойство подобных явлений, заключающихся в том, что для всех подобных систем существует безразмерные комплексы величин, которые сохраняют одно и тоже значение, эти комплексы носят название инвариантов (не изменяемые) или критериев подобия. При выводе формулы 2 был рассмотрен пример, в котором основное уравнение:

 

задано в комплексной форме. Если основное уравнение будет задано в дифференциальной форме, то все предыдущие результаты останутся прежними, при этом как показывается в общей теории подобия для нахождения критерия подобия, необходимо в исходном уравнении отбросить все индексы, знаки суммы, символы выражающие действия дифференцирования и т.п. ибо эти упрощающие не изменяемые константы подобия.

По этому основная ценность не интерпретируемых дифференциальных уравнений (Прим: процесса конвективного теплообмена Фурье-Киргоффа, движение вязкой капельной жидкости Новье-Стокса и др.) состоит в том, что они позволяют составить критерий подобия для описываемых ими процессов.

λ - коэфициент теплопроводности, с - удельная теплоемкость, ρ - плотность.

Проведем подобные преобразования: отбросив знаки суммирования и дифференцирования:

или критерий Фурье:

полученный комплекс являетс искомым критерием подобия, который называется критерием Фурье

А при выборе констант должно выполняться условие:

Все критерии подобия, в состав которых входит время называются критериями гомохромности, т.к. этими критериями определяется константа подобия (масштаб) времени через константы подобия других физических величин.

Теоремы подобия

1. По Ньютону: Подобные явления имеют численно одинаковые критерии подобия.

По Кирпичеву М.В.: У подобных явлений индикаторы подобия равны "1".

2. Количественные результаты опытов нужно представлять в виде уравнений выражающих зависимость между критерием подобия процесса, т.е. что любая зависимость между переменными характеризующей какое-либо явление может быть представлена в форме зависимости между критериями подобия составленными из этих элементов:

f(k₁,k₂,...,k_n)=0 - подобные зависимости называются критериальными уравнениями, в эти уравнения помимо критерия подобия могут входит симплексы, или так называемые параметрические критерии, представляющие собой отношение двух однородных величин.

В отличии от критериев подобия, составляемых из не однородных величин и называемых критериями-комплексами, критерии-симплексы получаются не как результаты обработки основных уравнений, а вытекают соответственно из подстановки задачи. Например если:

параметрический критерий или симплекс.

3. М.В. Кирпичева, А.А. Глухмана трактует о тех условиях, которые необходимы и достаточны для подобия двух явлений.

В соответствии с ней два явления подобны если они имеют подобные условия однозначности, и численно одинаковы определяющие критерии подобия.

Определяющими критериями подобия называют критерии которые составлены из параметров входящих в условия однозначности.

Условия однозначности: Понятие подобия применимо к таким физическим явлениям, которые качественно одинаковы как по форме, так и по содержанию, т.е. имеют одну физическую природу, развиваются под действием одинаковых сил и описываются одинаковыми по форме ДУ и краевыми условиями (условиями однозначности). В противном случае явления будут называться аналогичными, пример: теплопроводность и диффузия (аналогичны т.к. у них совершенно разная физическая природа).

Условия однозначности дают математическое описание всех частных особенностей рассматриваемой задачи и включают:

1. геометрические условия - определяющие размеры и форму тела или системы тел, где протекает процесс.

2. фактические свойства среды существенные для рассматриваемого процесса.

3. граничные условия которые описывают особенности процесса протекающего на границах системы с окружающей средой.

4. временные условия, показывающие особенности протекания рассматриваемого процесса во времени, для стационарных процессов временные условия отпадают.

Условия однозначности заданные в виде конкретных числовых значений в соединении с диф уравнением выделяют из всего класса процессов один конкретный процесс.

В этом случае решением диф. уравнения, если его удается получить справедливо только для заданных численных условий однозначности.

Естественно, что равенство определяющих критериев подобия влечет за собой равенство всех остальных критериев в состав которых входят величины не предусмотренные условиями однозначности, так называемых не определяющих критериев. Т.о. каждый из не определенных критериев будет представлять собой однозначную функцию совокупности определяющих критериев. Т.е. если k₁, k₂, k_n - определяющие критерии, а k - не определяющий, то: k=f(k₁,k₂,...,k_n).

Это положение имеет большое значение для данных опыта, и представляет собой центральное звено всей теории подобия.

Теория подобия позволяет полно ответить на вопрос о том, как надо ставить эксперимент, что нужно изменять во время опыта, как нужно обрабатывать полученные результаты, и какие явления будут подобны изученным.

Во время опыта нужно измерять все те величины, которые входят в критерий подобия (это вытекает из первой теории подобия). Результат подобия следует обрабатывать в форме критериальных уравнений, при этом определяющие критерии являются аргументами, а не определяющие - функциями (эта составляющая второй теоремы подобия). На вопрос о том какие объекты будут подобны исследуемому отвечает теорема Кирпичева-Гухмана.

Для удобства критериальные уравнения представляют в форме степенной зависимости:

Это обусловлено тем, что в логарифмических координатах степенная зависимость изображается прямой линией, при этом показатель т определяется как тангенс угла наклона прямой, а коэффициент с - как отрезок оси абсцисс.