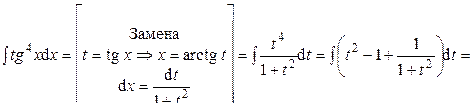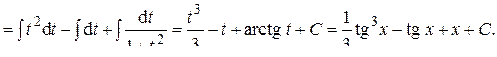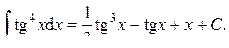Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование простых дробейСодержание книги
Поиск на нашем сайте
Задача интегрирования рациональной дроби сводится к умению интегрирования только правильных рациональных дробей, так как интегрирование целой части дроби (многочлена) – задача не сложная. Если решена задача разложения правильной дроби на сумму простых дробей, то дальше надо уметь интегрировать простые дроби. Покажем, как интегрировать простые дроби (четыре типа).
I тип.
II тип.
III тип.
Интегрирование дроби IV типа проводится аналогично интегрированию дроби III типа.
Пример 22. Найти интеграл от дроби III типа:
(D = 16 – 52 < 0 Þ дробь III типа)
Ответ: Пример 23. Найти интеграл от дроби IV типа:
Ответ:
Итак, любая рациональная дробь интегрируема. Для этого необходимо выполнить следующие шаги: 1) Выделить целую часть дроби, если дробь является неправильной, т.е. представить в виде:
где T m – n (x) и R r (x) – многочлены степени m – n и r соответственно (причём r < n). 2) Разложить правильную рациональную дробь 3) Вычислить интегралы от многочлена T m – n (x) и каждой из простых дробей, полученных на шаге 2). Пример 24. Найти интеграл 1) Дробь
Поэтому можно записать:
2) Полученную правильную дробь
Отсюда следует: Значит, подынтегральную рациональную дробь можем представить в виде:
3) Найдём интеграл:
Ответ:
Интегрирование тригонометрических выражений 1) Интеграл вида а) Если n – чётное число и m – чётное, то подынтегральное выражение преобразуют с помощью формул:
б) Если одно из чисел m или n – нечётное, то выполняют замену: t = sin x, если n – нечётное; t = cos x, если m – нечётное. Эта замена приводит к интегрированию степенных интегралов или рациональных дробей. в) Если оба числа m и n – нечётные, то интеграл берется как в случае замены: t = sin x, так и t = cos x. Пример 25. Вычислить интеграл:
Ответ: Пример 26. Вычислить интеграл:
Ответ: Пример 27. Вычислить интеграл:
Ответ:
2) Интегралы вида:
где Такие интегралы находят после предварительного применения формул:
Пример 28. Вычислить интеграл:
Ответ:
3) Интеграл вида:
Такие интегралы приводятся к интегралам от рациональной дроби с помощью замены:
Пример 29. Вычислить интеграл:
Ответ: 4) Интегралы вида: Такие интегралы находят сведением к интегралу от рациональной дроби с помощью замены:
Пример 30. Вычислить интеграл:
Ответ: 5) Интегралы вида: Такие интегралы находят после предварительного применения формул:
или с помощью замены:
или Пример 31. Вычислить интеграл:
Ответ:
|
|||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 105; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.73.150 (0.01 с.) |

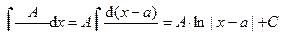
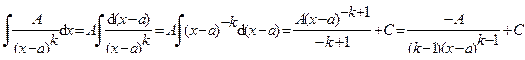
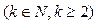
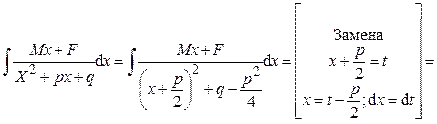
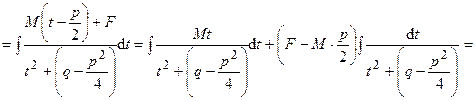
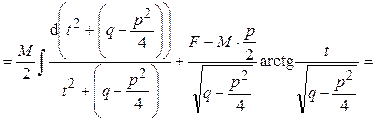
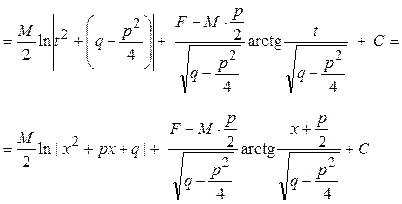
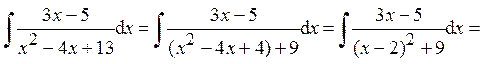
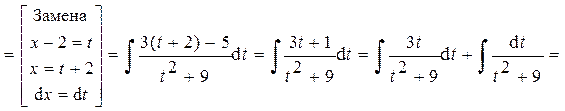
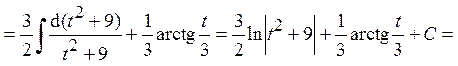
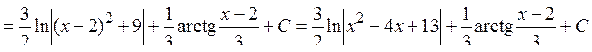 .
.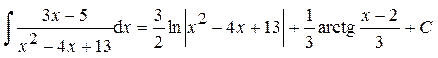 .
.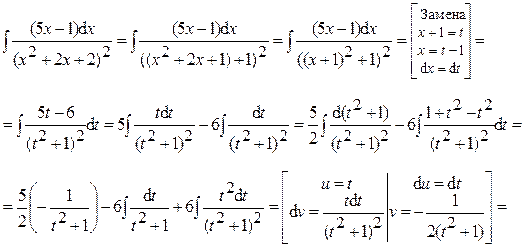
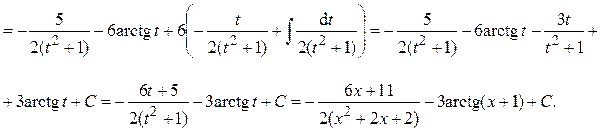
 .
.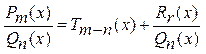 ,
,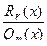 на сумму простых дробей.
на сумму простых дробей.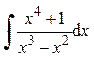
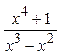 – неправильная рациональная дробь. Выделим её целую часть:
– неправильная рациональная дробь. Выделим её целую часть: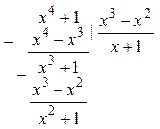
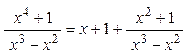 .
.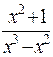 разложим на сумму простых дробей:
разложим на сумму простых дробей: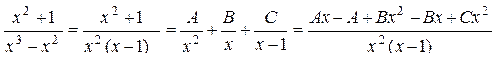
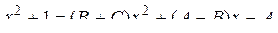
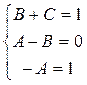
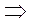
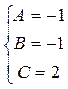

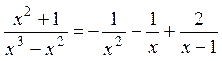 .
.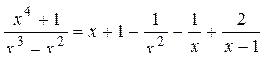 .
.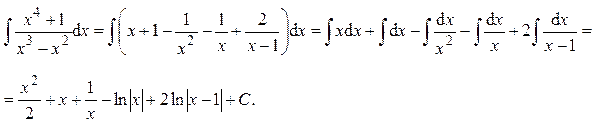
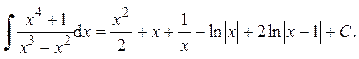
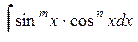
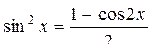 ,
, 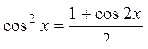
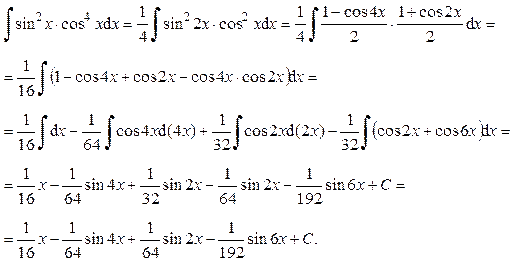
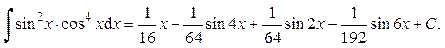
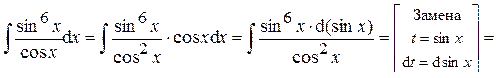
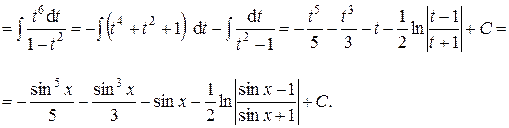
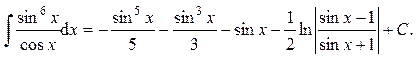
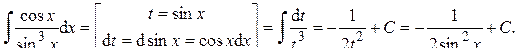
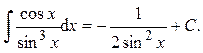
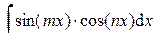 ;
; 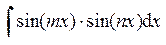 ;
; 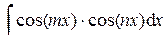

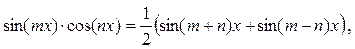
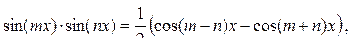
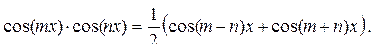
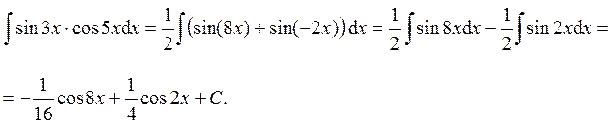
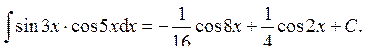
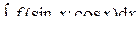 , где f (u; v) – рациональная функция двух переменных.
, где f (u; v) – рациональная функция двух переменных.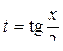 ;
;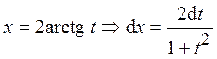 ;
;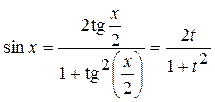 ;
; 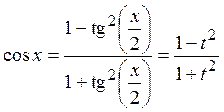 .
.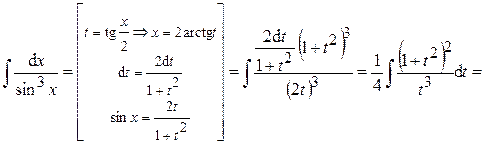
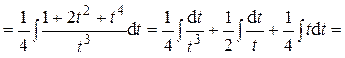
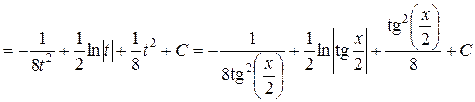 .
.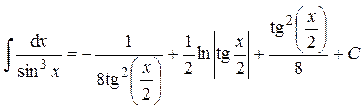 .
.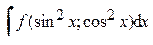 , где f (u; v) – рациональная функция двух переменных.
, где f (u; v) – рациональная функция двух переменных.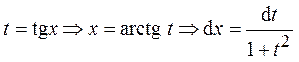
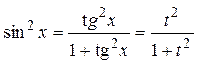 ;
; 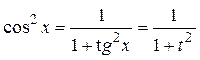
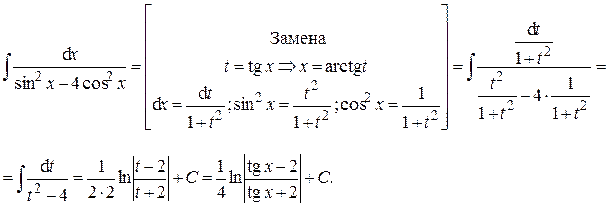
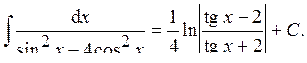
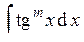 ;
; 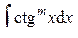 , где
, где 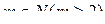 .
.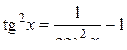 ;
; 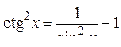
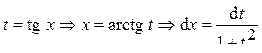 ;
;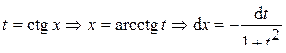 .
.