Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема 1 (связь дифференцируемости с существованием производной)
Функция y = f (x) дифференцируема в точке x Î D (f) тогда и только тогда, когда она имеет в этой точке производную f ' (x). При этом f ' (x) = A. Доказательство. 1) Необходимость: Дано: y = f (x) дифференцируема в точке х. Доказать: A = f ' (x). Так как функция y = f (x) дифференцируема в точке х, то по определению D y = A × D x + где Разделим это равенство на D x ≠ 0:
Перейдём к пределу при D x ® 0:
Необходимость доказана. 2) Достаточность: Дано: f ' (x) – существует Доказать: f (x) дифференцируема. Так как существует f ' (x)=
где Умножим это равенство на D x:
Достаточность доказана. Теорема 2 (связь дифференцируемости с непрерывностью функции) Если функция y = f (x) дифференцируема в точке x Î D (f), то она непрерывна в этой точке. Доказательство. Так как функция дифференцируема в точке x, то её приращение в этой точке можно представить в виде: D y = A × D x + где A = f ' (x) и Найдём предел от D y при D x ® 0:
Отсюда следует, что по определению 2 непрерывности функции в точке функция y = f (x) непрерывна в точке x. Замечание. Обратное теореме 2 утверждение не всегда верно.
Правила дифференцирования Теорема 3. Если функции U (x) и V (x) дифференцируемы в точке x, то функция U (x) ± V (x) дифференцируема в точке x и её производная вычисляется по формуле: (U (x) ± V (x))' = (U (x))' ± (V (x))'. Доказательство: Рассмотрим функцию y = U (x) ± V (x). Тогда D y = D U ± D V. Разделим на D x и перейдём к пределу при D x ® 0:
так как по условию теоремы функции U (x) и V (x) дифференцируемы. Значит, (U (x) ± V (x))' = U '(x) ± V '(x). Теорема доказана. Теорема 4. Если функции U (x) и V (x) дифференцируемы в точке х, то функция (U (x)× V (x)) дифференцируема в точке х и её производная вычисляется по формуле: (U (x) × V (x))' = (U (x))'× V (x) + U (x) × (V (x))'. Доказательство. Рассмотрим функцию D y = (U +D U)(V +D V) – U × V = U × V + U ×D V + V ×D U + D U ×D V – U × V = = U ×D V + V ×D U + D U ×D V. Разделим D y на D x и перейдем к пределу при D x ® 0:
так как по условию функции U (x) и V (x) дифференцируемы, а значит Следовательно,
(U (x)× V (x))' = U ' (x) × V (x) + U (x) × V ' (x). Теорема доказана. Следствия: а) Если U (x), V (x) и W (x) дифференцируемы в точке х, то функция (U (x)× V (x) × W (x)) дифференцируема в точке х и её производная вычисляется по формуле:
(U × V × W)' = U '× V × W + U × V '× W + U × V × W '. б) Производная постоянной, умноженной на дифференцируемую функцию, равна этой постоянной, умноженной на производную функции:
(C× U (x))' = C× U ' (x). Теорема 5. Если функции U (x) и V (x) дифференцируемы в точке х и V (x) ≠ 0, то функция
Доказательство. Рассмотрим функцию Разделим D y на D x и перейдём к пределу при D x ® 0:
Значит,
Теорема доказана. Теорема 6 (производная сложной функции). Если функция f (u) дифференцируема в точке u, а функция u (x) дифференцируема в точке x, причём u = u (x), тогда сложная функция f (u (x)) дифференцируема в точке x и её производная вычисляется по формуле: (f (u (x)))' = f '(u) × u ' (x). Доказательство. Рассмотрим функцию y = f (u). Так как функция f (u) дифференцируема в точке u, то её приращение можно записать в виде:
где Разделим на D x и перейдём к пределу при D x ® 0:
Если D x ® 0, то D u ® 0, так как u (x) дифференцируема, а значит непрерывна, т.е. (f (u (x)))' = f ' (u) × u ' (x). Теорема доказана.
|
|||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 247; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.143.181 (0.012 с.) |
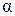 (D x) × D x,
(D x) × D x,
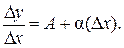 .
.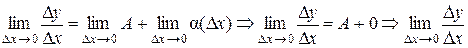 существует, а значит f ' (x) = A.
существует, а значит f ' (x) = A.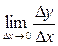 , то по свойству предела можно записать:
, то по свойству предела можно записать: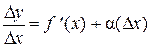 ,
,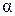 (D x) ® 0 при D x ® 0.
(D x) ® 0 при D x ® 0.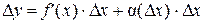 Þ функция y = f (x), дифференцируема в точке х.
Þ функция y = f (x), дифференцируема в точке х.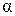 (D x) × D x,
(D x) × D x,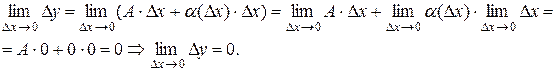
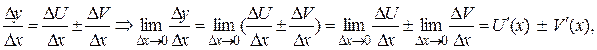
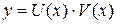 . Найдём её приращение
. Найдём её приращение
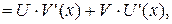
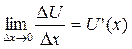 ,
, 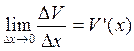 и
и 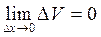 .
.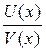 дифференцируема в точке х и её производная вычисляется по формуле:
дифференцируема в точке х и её производная вычисляется по формуле: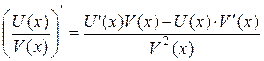 .
.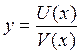 . Найдём её приращение
. Найдём её приращение 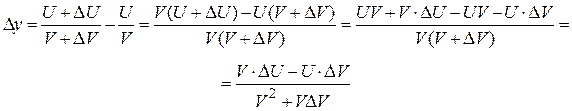
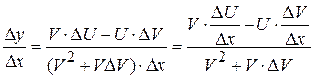 ,
,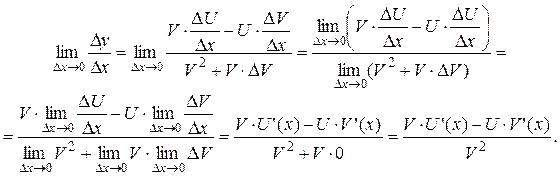
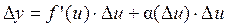 ,
,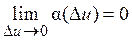 .
.