
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференцирование функции, заданной неявноСодержание книги
Поиск на нашем сайте
Пусть функция Пример. Найти y ', если функция y задана уравнением: x 3 + y 3 – xy = 0 Решение. 3 x 2 + 3 y 2 × y ’ – y – xy ’ = 0 y’(3y2 – x) = y – 3x2
Ответ: Производные показательной и степенной функций Теорема 7. Степенная функция y = x a (aÎR) дифференцируема при любом x ÎR и справедлива формула: (x a)' = a × x a – 1. Доказательство. Прологарифмируем равенство y = x a, предполагая x > 0: ln y = a× ln x Получили уравнение от x и y, задающее функцию y = x a неявно. Найдём производные от обеих частей равенства:
Выразим отсюда y ':
Подставим в полученное равенство y = x a:
Теорема доказана. Теорема 8. Показательная функция y = ax (a > 0, a ≠ 1) дифференцируема при любом x ÎR и справедлива формула: (ax)' = ax × ln a Доказательство. Прологарифмируем равенство y = ax: ln y = x ln a. Получили уравнение от x и y, задающее функцию y = ax неявно. Найдём производные от обеих частей равенства:
Выразим отсюда y ': y ' = y × ln a. Подставим в полученное равенство y = ax : (ax)' = ax × ln a Теорема доказана. Замечание. В частном случае, при a = e полученная формула в теореме 8 принимает вид: (ex)' = ex × ln e или (ex)' = ex. Теорема 9. Если функции U (x) и V (x) дифференцируемы в точке x, то показательно-степенная функция y = (U (x)) V ( x ) дифференцируема в точке x и справедлива формула:
Доказательство можно выполнить с помощью логарифмирования равенства y = (U (x)) V ( x ) по основанию логарифма e и дальнейшего дифференцирования обеих частей полученного равенства.
Производные обратных тригонометрических функций Теорема 10. Функция y = arcsin x дифференцируема при любом x Î(–1;1) и справедлива формула:
Доказательство: Функция y = arcsin x определена при x Î[–1;1] и область ее значений
Выразим из полученного равенства y ':
Но Поэтому Следовательно, получаем:
Теорема 11. Функция y = arсcos x дифференцируема при x Î(–1;1) и справедлива формула:
Теорема 12. Функция y = arctg x дифференцируема при x Î(–¥;+¥) и справедлива формула:
Теорема 13. Функция y = arcсtg x дифференцируема при x Î(–¥;+¥) и справедлива формула:
Теоремы 11, 12, и 13 доказываются аналогично теореме 10.
Дифференциал функции Пусть функция y = f (x) дифференцируема в точке x, тогда её приращение можно записать в виде двух слагаемых, первое из которых линейно относительно D x, а второе слагаемое – бесконечно малая величина при D x ® 0 (более высокого порядка малости по сравнению с D x):
где Определение 4. Слагаемое
d y = y ' (x)× D x. Если x – независимая переменная, то справедливо равенство D x = d x, так как (x)' = 1. Тогда формула для дифференциала записывается:
d y = y ' (x)× d x. Так как второе слагаемое приращения функция – малая величина более высокого порядка малости по сравнению с D x, то между приращением функции и её дифференциалом можно приближённо поставить знак равенства. Это равенство тем точнее, чем меньше D x. На основе этого приближённого равенства получается приближённое представление значения дифференцируемой функции:
Пример. Вычислить приближённо Решение. Рассмотрим функцию возьмём x 0 = 4, приращение D x = 0,08,
где D << 0,08.
|
|||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.131.156 (0.008 с.) |

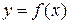 задана неявно уравнением
задана неявно уравнением 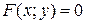 . Дифференцируя это равенство по x по правилу дифференцирования сложной функции, находим из полученного равенства y '.
. Дифференцируя это равенство по x по правилу дифференцирования сложной функции, находим из полученного равенства y '.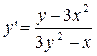
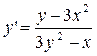 .
.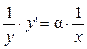
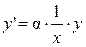
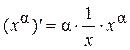
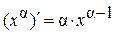
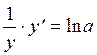
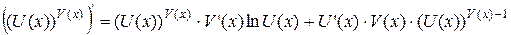 .
.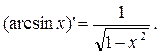
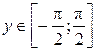 . Она монотонно возрастает на всей области её определения, поэтому имеет обратную функцию x = sin y. Уравнение x = sin y можно рассматривать как неявное задание функции y = arcsin x. Найдём производную от обеих частей уравнения:
. Она монотонно возрастает на всей области её определения, поэтому имеет обратную функцию x = sin y. Уравнение x = sin y можно рассматривать как неявное задание функции y = arcsin x. Найдём производную от обеих частей уравнения: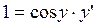 .
.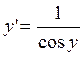 .
. при
при 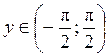 .
.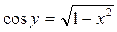 , так как
, так как 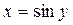 .
.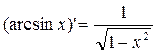 .
. .
.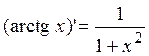 .
.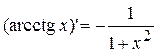 .
. 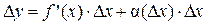 ,
,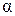 (D x) ® 0 при D x ® 0.
(D x) ® 0 при D x ® 0.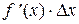 называется главной линейной относительно D x частью приращения функции y = f (x), называемой дифференциалом этой функции. Дифференциал обозначается
называется главной линейной относительно D x частью приращения функции y = f (x), называемой дифференциалом этой функции. Дифференциал обозначается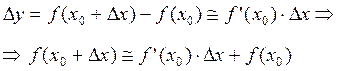
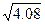
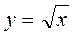 . В качестве начальной точки
. В качестве начальной точки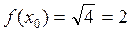 и подставим в формулу:
и подставим в формулу: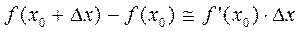
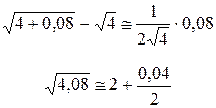
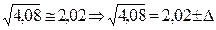 ,
,


