
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрический смысл дифференциала
Рассмотрим график дифференцируемой функции y = f (x) в некоторой окрестности точки x 0 (рис. 6):
Рис. 6 Из D M 0 AN AN = M 0 A ×tg a = D x × f '(x 0) = d y. Итак: дифференциал функции y = f (x) в точке x 0 равен приращению ординаты касательной (AN), проведённой к кривой y = f (x) в точке (x 0; f (x 0)), при переходе от x 0 к x 0+D x (от точки М 0 в точку М). Инвариантность формы дифференциала Теорема 14. Пусть функция y = f (u) дифференцируема в точке u, а функция u = u (x) дифференцируема в соответствующей точке x (u = u (x)). Тогда для сложной функции y = f (u (x)) справедливо равенство:
d y = f '(u)d u = y '(x)d x. Доказательство. Сложная функция y = f (u (x)) является дифференцируемой в точке x. Поэтому справедливо равенство:
d y = y '(x)d x. Но так как функция y (x) = f (u (x)) сложная, то
y ' (x) = f ' (u) × u ' (x). Поэтому d y = y '(x)d x = f '(u)× u '(x)d x = f '(u)×d u, так как по условию теоремы функция u = u (x) дифференцируема в точке x, следовательно, d u = u ' (x)×d x. Теорема доказана.
Производные и дифференциалы высших порядков Если функция y = f (x) дифференцируема на некотором промежутке, то она имеет на этом промежутке производную y ' = f ' (x), которая в свою очередь может иметь производную: (y ')' = (f '(x))' = y '', называемую второй производной функции y = f (x). Она обозначается:
Может случиться, что новая функция y ''(x) имеет производную, тогда она называется третьей производной функции y = f (x) и обозначается:
Производная “ n ”-го порядка функции y = f (x) обозначается:
Дифференциалом второго порядка функции y = f (x) в точке x называется выражение, обозначаемое d2 y и вычисляемое по формуле:
если x – независимая переменная. Дифференциал третьего порядка функции y = f (x):
если x – независимая переменная, и т.д. Замечание. Дифференциал уже второго порядка не обладает свойством инвариантности формы.
СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ Теорема 1. Если функция f (x) непрерывна на отрезке [ a; b ], то она достигает на этом отрезке своих наименьшего m и наибольшего M значений, т.е. для любых x Î [ a; b ] выполняется неравенство: m ≤ f (x) ≤ M. Теорема 2. Если функция f (x) непрерывна на отрезке [ a; b ], то для любого числа С, удовлетворяющего неравенству m ≤ С ≤ M, на отрезке [ a; b ] найдётся хотя бы одна точка х 0, в которой выполняется равенство:
f (х 0) = С. Теорема 3. Если функция f (x) непрерывна на отрезке [ a; b ] и на концах этого отрезка имеет значения различных знаков, то существует хотя бы одна точка х 0 Î (a; b), в которой выполняется равенство: f (х 0) = 0. Теорема Ролля Теорема 4 (теорема Ролля). Если функция f (x) определена на отрезке [ a; b ] и выполнены следующие условия: · f (x) непрерывна на отрезке [ a; b ]; · f (x) дифференцируема на интервале (a; b); · f (a) = f (b), то внутри этого отрезка [ a; b ] найдется хотя бы одна точка х 0, в которой выполняется равенство: f '(х 0) = 0. Доказательство. Так как f (x) непрерывна на отрезке [ a; b ], то она достигает на этом отрезке своих наименьшего m и наибольшего M значений. Возможны два случая: m = M и m < M. · Если m = M, то f (x) = const = m = M. Тогда f '(x) = 0 при любом x Î [ a; b ]. Следовательно, в этом случае теорема верна и при этом в качестве х 0 можно рассматривать любое значение x Î [ a; b ]. · Если m < M, то исходя из условия f (a) = f (b), по крайней мере одно из чисел m или M не равно f (a) = f (b). Для определённости предположим, что M – наибольшее значение f (x) достигается не на концах отрезка [ a; b ], а в некоторой внутренней точке х 0 Î (a; b). Тогда в точке х 0 для приращения функции справедливо неравенство: D y = f (х 0 + D x) – f (х о) ≤ 0, так как f (х 0) = M – наибольшее значение f (x) на отрезке [ a; b ] и D x такое, что х 0 + D x Î [ a; b ]. · Если D x > 0, то · Если D x < 0, то Так как по условию теоремы функция f (x) дифференцируема при x Î (a; b), то в точке х о существует производная. Значит справедливы равенства: f ' (х 0 + 0) = f ' (х 0 – 0) = f ' (х 0) = 0. Теорема доказана.
|
|||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 123; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.68.14 (0.007 с.) |




 ,
, ,
, и существует
и существует 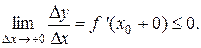
 и существует
и существует 



