
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование поведения функцийСодержание книги
Поиск на нашем сайте
Асимптоты плоской кривой Определение 1. Если точка M (x; y) перемещается по кривой y = f (x) так, что хотя бы одна из координат точки стремится к ¥ и при этом расстояние от этой точки до некоторой прямой стремится к 0, то эта прямая называется асимптотой кривой y = f (x). Асимптоты бывают двух видов: вертикальные и наклонные. Определение 2. Прямая x = a называется вертикальной асимптотой кривой y = f (x), если хотя бы один из односторонних пределов Замечание. Если прямая x = a является вертикальной асимптотой кривой y = f (x), то в точке x = a функция f (x) имеет разрыв второго рода. Наоборот, если в точке x = a функция f (x) имеет разрыв второго рода, то прямая x = a является вертикальной асимптотой кривой y = f (x). Определение 3. Прямая
где Теорема 1. Для того чтобы кривая y = f (x) имела наклонную асимптоту при
Доказательство. Ограничимся случаем Необходимость. Пусть y = kx + b – наклонная асимптота при
Убедимся в существовании конечных пределов:
Необходимость доказана. Достаточность. Пусть существуют конечные пределы Тогда по свойству конечных пределов второй предел можно переписать в виде:
где Отсюда получаем:
где Достаточность доказана. Пример 1. Найти асимптоты кривой Решение. 1) D (y) = (–¥;–1) È (–1;1) È (1;+ ¥). 2) Точки x = –1 и x = 1 являются точками разрыва второго рода, так как:
Поэтому прямые x = –1 и x = 1 являются вертикальными асимптотами. 3) Вычислим пределы:
Отсюда следует, что при Найдём наклонную асимптоту при Вычисляя те же пределы при Ответ: x = ± 1 – вертикальные асимптоты y = x – наклонная асимптота при x ® ±¥. Монотонность функции Определение 4. Функция y = f (x) называется возрастающей (убывающей) на промежутке (a; b), если для любых x 1 и x 2, принадлежащих этому промежутку, из условия x 2 > x 1 следует неравенство:
f (x 2) > f (x 1) (f (x 2) < f (x 1)).
Определение 5. Функция y = f (x) называется монотонной на промежутке (a; b), если она на этом промежутке является только возрастающей или только убывающей. Теорема 2 (достаточные условия монотонности). Если функция y = f (x) дифференцируема на промежутке (a; b) и f ’ (x) > 0 (f ’ (x) < 0) для любых x Î (a; b), то функция возрастает (убывает) на этом промежутке. Доказательство. Возьмём любые два значения x 1 и x 2 из промежутка (a; b). Для определённости предположим, что x 2 > x 1. На отрезке [ x 1; x 2] функция y = f (x) непрерывна и дифференцируема (из условия теоремы). Следовательно, она удовлетворяет теореме Лагранжа на отрезке [ x 1; x 2], т.е. существует хотя бы одна точка c Î (x 1; x 2), в которой выполняется равенство: f (x 2) – f (x 1) = f ' (c) × (x 2 – x 1). Если f '(x) > 0 для любых x Î(a; b), то f '(c) > 0. Поэтому f (x 2) – f (x 1) > 0, т.е. из условия x 2 > x 1 следует неравенство f (x 2) > f (x 1). А так как x 1 и x 2 –любые значения из промежутка (a; b), то функция y = f (x) возрастает на этом промежутке. Если Теорема доказана. Экстремумы функции Определение 6. Функция y = f (x) имеет в точке x 0Î D (f) максимум y m ax (минимум y min), если существует такая окрестность точки x 0, в которой для всех x выполняется неравенство:
f (x 0) > f (x) (f (x 0) < f (x)). Определение 7. Точки максимума и минимума функции называются точками экстремума функции. Теорема 3 (необходимое условие экстремума). Если функция y = f (x) имеет экстремум в точке x 0, то в этой точке производная функции равна нулю или не существует. Доказательство. 1)Для определённости рассмотрим случай, когда функция y = f (x) в точке x 0 имеет максимум и в этой точке существует производная. Тогда из определения максимума для любого x, принадлежащего окрестности точки x 0 f (x 0) > f (x). Отсюда следует, что для любого D x ≠ 0 справедливо неравенство: f (x 0+D x) – f (x 0) < 0. Разделим это неравенство на D x, получим: при D x > 0: при D x < 0:
Перейдём к пределам:
Так как
Аналогично рассматривается случай, когда x 0 – точка минимума. 2) Если f '(x 0) не существует или равна ¥, то точка x 0 может быть точкой экстремума функции. Например, функция y =
Рис. 9
Теорема доказана. Теорема 4 (достаточное условие экстремума). Если функция y = f (x) непрерывна в точке x 0, дифференцируема в некоторой её окрестности, за исключением может быть самой этой точки, f ’ (x 0) = 0 или не существует и при переходе x через точку x 0 производная f '(x) изменяет знак, то точка x 0 является точкой экстремума. Если при этом знак f '(x) меняется с + на –, то x 0 – точка максимума, с – на +, то x 0 – точка минимума. Доказательство. Пусть f '(x) при переходе x через точку x 0 изменяет знак с + на –, т.е. f '(x) > 0 при x Î (x 0 – d; x 0) и f '(x) < 0 при x Î (x 0; x 0 + d), где d > 0 (рис. 10).
Рис. 10
1) Пусть x Î (x 0 – d; x 0). На отрезке [ x; x 0] функция y = f (x) удовлетворяет теореме Лагранжа. Значит, на интервале (x; x 0) найдётся хотя бы одна точка c 1, в которой выполняется равенство: f (x) – f (x 0) = f '(c 1)×(x – x 0), где c 1Î (x 0 – d; x 0). Так как f '(c 1) > 0 и x – x 0 < 0, то f (x) – f (x 0) < 0.
2) Пусть
f (x) – f (x 0) = f ’ (c 2)×(x – x 0), где c 2 Î (x 0; x 0 + d). Так как f '(c 2) < 0 и x – x 0 > 0, то f (x) – f (x 0) < 0.
Следовательно, для любого x Î (x 0 – d; x 0 + d) выполняется неравенство: f (x 0) > f (x). Отсюда следует, что точка x 0 является точкой максимума функции y = f (x). Аналогично рассматривается случай, когда Теорема доказана.
|
||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 140; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

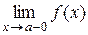 или
или 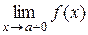 равен +¥ или – ¥.
равен +¥ или – ¥.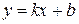 называется наклонной асимптотой кривой
называется наклонной асимптотой кривой 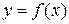 при
при 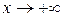 (или
(или 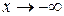 ), если функцию f (x) можно представить в виде:
), если функцию f (x) можно представить в виде: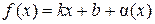 ,
,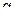 (x) – бесконечно малая функция при
(x) – бесконечно малая функция при 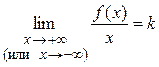 и
и 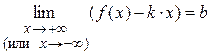
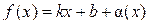 , где
, где 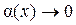 при
при 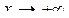 .
.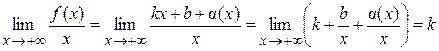 .
.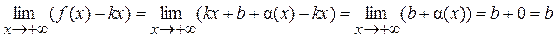 .
.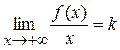 и
и 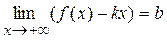 .
.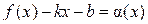 ,
, 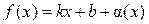 ,
,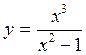 .
.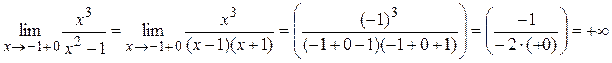
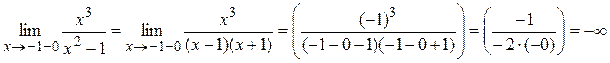
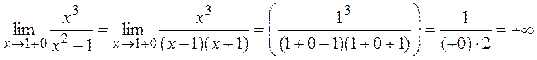
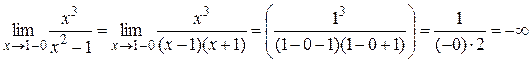
 , k = 1.
, k = 1.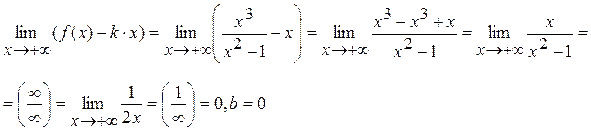
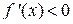 для любых
для любых 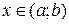 , то
, то 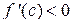 . Поэтому
. Поэтому 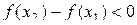 , то есть из условия x 2 > x 1 следует неравенство f (x 2) < f (x 1). Так как x 1 и x 2 любые значения из промежутка (a; b), то функция y = f (x) убывает на этом промежутке.
, то есть из условия x 2 > x 1 следует неравенство f (x 2) < f (x 1). Так как x 1 и x 2 любые значения из промежутка (a; b), то функция y = f (x) убывает на этом промежутке.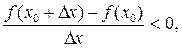
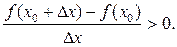
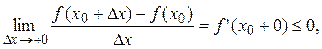
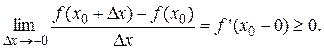
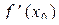 существует, то:
существует, то: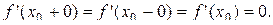
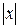 имеет минимум при x = 0, хотя y '(0) не существует (рис. 9).
имеет минимум при x = 0, хотя y '(0) не существует (рис. 9).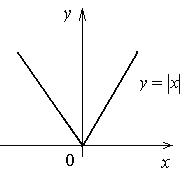
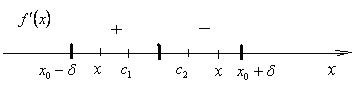
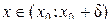 . На отрезке
. На отрезке 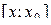 функция
функция 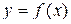 также удовлетворяет теореме Лагранжа. Значит на интервале (x 0; x) найдётся хотя бы одна точка с 2, в которой выполняется равенство:
также удовлетворяет теореме Лагранжа. Значит на интервале (x 0; x) найдётся хотя бы одна точка с 2, в которой выполняется равенство: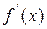 при переходе x через точку x 0 изменяет знак с – на +. При этом точка x 0 является точкой минимума функции
при переходе x через точку x 0 изменяет знак с – на +. При этом точка x 0 является точкой минимума функции 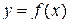 .
.


