
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение функции одной переменнойСодержание книги
Поиск на нашем сайте Определение. Пусть даны два множества X и Y. Если каждому элементу x из множества X по некоторому правилу f соответствует единственный элемент y из множества Y, то говорят, что на множестве X определена функция y = f (x) с областью определения X = D (f) и областью изменения Y = E (f). При этом x считают независимой переменной, или аргументом функции, а y – зависимой переменной или функцией. Частным значением функции y = f (x) при фиксированном значении аргумента x = x0 называют y 0 = f (x 0). Графиком функции y = f (x) называют геометрическое место точек M (x; f (x)) на плоскости Oxy, где x Î D (f) и f (x) Î E (f).
2. Способы задания функции 1) Аналитический способ – способ задания функции с помощью формулы. Различают несколько способов аналитического задания функции: а) Функция задана явно формулой y = f (x). Например: б) Функция задана неявно уравнением, связывающем x и y: F (x; y) = 0. Например:
которые имеют область определения в) Функция задана параметрически с помощью некоторого параметра t, причём и аргумент x, и функция y зависят от этого параметра:
Например: можно задать окружность
2) Табличный способ задания функции – например, таблицы Брадиса задают функции y = sin x, y = cos x и др. 3) Графический способ задания функции, когда зависимость функции от её аргумента задаётся графически.
Сложная и обратная функции Определение 1. Пусть функция y = f (U) определена на множестве D (f), а функция U = g (x) определена на D (g), причём E (g) Тогда функция y = F (x) = f (g (x)) называется сложной функцией (или функцией от функции, или суперпозицией функций f и g). Определение 2. Пусть задана функция y = f (x) взаимно однозначно отображающая множество X = D (f) на множество Y = E (f). Тогда функция x = g (y) называется обратной к функции y = f (x), т. е. любому y Замечание. Графики функций y = f (x) и x = g (y) представляют одну и ту же кривую. Если же у обратной функции независимую переменную обозначить x, а зависимую y, то графики функций y = f (x) и y = g (x) будут симметричны относительно биссектрисы первого и третьего координатных углов.
Элементарные функции Основные элементарные функции: y = const (постоянная функция), D (y) = R; E (y) = c.
y = y = y = Тригонометрические функции: y = sin x, D (y) = R, E (y) = y = cos x, D (y) = R, E (y) = y = tg x, D (y) = y = ctg x, D (y) = Обратные тригонометрические функции: y = arcsin x, D (y) = y = arccos x, D (y) = y = arctg x, D (y) = R, E (y) = y = arcctg x, D (y) = R, E (y) = Элементарной функцией называется функция, составленная из основных элементарных функций с помощью конечного числа операций сложения, вычитания, умножения, деления и суперпозиции. Например:
Графики обратных тригонометрических функций:
ПРЕДЕЛ ФУНКЦИИ 1. Предел функции в конечной точке x0
Определение 2. d-Окрестностью точки x 0называется интервал (
Определение 3. Проколотой d-окрестностью точки x 0 называется d-окрестность точки x 0 без самой точки x 0:
Определение 4. Число А называется пределом функции f (x) при x ® x 0, если для любого малого числа ε > 0 существует такое малое число Итак: Односторонние пределы Определение 5. Число А называется правым (левым) пределом функции y = f (x) в точке x 0, если для любого малого числа ε > 0 найдётся другое малое число При этом используют следующие обозначения:
Замечание 1. Если f (x) имеет в точке x 0, предел равный А, то существуют
Замечание 2. Если f (x) имеет в точке x 0 правый
Замечание 3. Если f (x) имеет в точке x 0 правый
|
||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

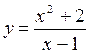 , где D (y) = (– ∞;1)
, где D (y) = (– ∞;1) 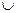 (1;+∞).
(1;+∞).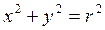 – уравнение окружности с центром в начале координат и радиусом r. Если из этого уравнения выразить y через x, то получится две функции:
– уравнение окружности с центром в начале координат и радиусом r. Если из этого уравнения выразить y через x, то получится две функции: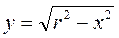 и
и 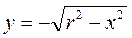 ,
,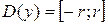 , а области значений этих функций будут: для первой –
, а области значений этих функций будут: для первой –  , для второй –
, для второй – 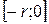 .
.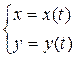
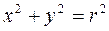 с помощью параметрических уравнений:
с помощью параметрических уравнений: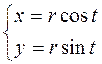
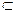 D (f).
D (f).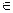 E (f) соответствует единственное значение x
E (f) соответствует единственное значение x 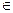 D (f), при котором верно равенство y = f (x).
D (f), при котором верно равенство y = f (x).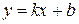 (линейная функция), D (y) = R; E (y) = R.
(линейная функция), D (y) = R; E (y) = R.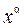 (степенная функция), α Î R, E (y), D (y) зависят от α.
(степенная функция), α Î R, E (y), D (y) зависят от α.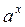 (показательная функция), a > 0, a ≠ 1, D (y) = R, E (y) = (0;+∞).
(показательная функция), a > 0, a ≠ 1, D (y) = R, E (y) = (0;+∞).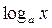 (логарифмическая функция)), a > 0, a ≠ 1, D (y) = (0;+∞), E (y) = R.
(логарифмическая функция)), a > 0, a ≠ 1, D (y) = (0;+∞), E (y) = R.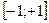 .
.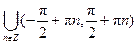 , E (y) = R.
, E (y) = R.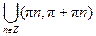 , E (y) = R.
, E (y) = R.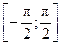 .
.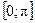 .
.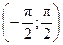 .
.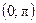 .
.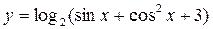 – элементарная функция.
– элементарная функция.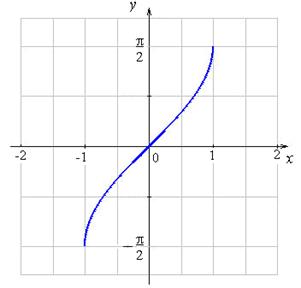 Рис. 1
Рис. 1
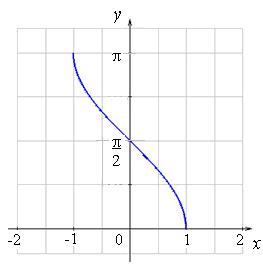 Рис. 2
Рис. 2
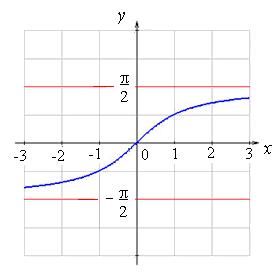 Рис. 3
Рис. 3
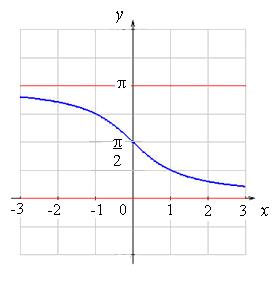 Рис. 4
Рис. 4
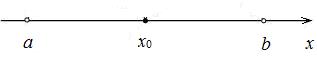
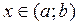 .
.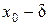 ;
; 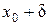 ), длина которого 2d, симметричный относительно x 0:
), длина которого 2d, симметричный относительно x 0: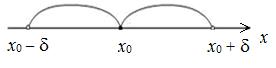
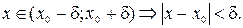
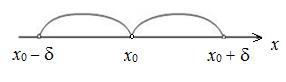
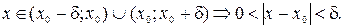
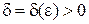 , что для любого x, принадлежащего D(f) и проколотой δ-окрестности точки x 0, т.е.
, что для любого x, принадлежащего D(f) и проколотой δ-окрестности точки x 0, т.е. 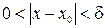 , выполняется неравенство:
, выполняется неравенство: 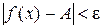 .
.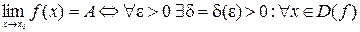 и
и 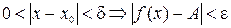 .
.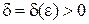 – такое, что для всех
– такое, что для всех 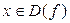 и лежащих в правой (левой) окрестности точки x 0, т.е.
и лежащих в правой (левой) окрестности точки x 0, т.е. 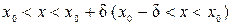 , справедливо неравенство:
, справедливо неравенство: 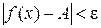 .
.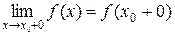 – для правого предела.
– для правого предела.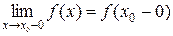 – для левого предела.
– для левого предела.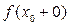 и
и 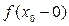 и справедливо равенство:
и справедливо равенство: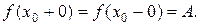 .
.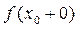 и левый
и левый 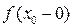 пределы, равные между собой, то в точке
пределы, равные между собой, то в точке 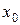 функция f (x) имеет предел, равный числу:
функция f (x) имеет предел, равный числу: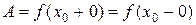 .
.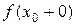 и левый
и левый 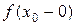 пределы, но они не равны между собой, то в точке x 0 функция f (x) не имеет предела.
пределы, но они не равны между собой, то в точке x 0 функция f (x) не имеет предела.


