
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие неопределённого интегралаСодержание книги
Поиск на нашем сайте
Определение 2. Множество всех первообразных для данной функции f (x) на интервале (a; b) называется неопределённым интегралом функции f (x) на этом интервале и обозначается символом:
В обозначении Теорема 2. Если функция f (x) непрерывна на промежутке (a; b), то она имеет на промежутке (a; b) первообразную и неопределённый интеграл. Замечание. Операция нахождения неопределённого интеграла от данной функции f (x) на некотором промежутке носит название интегрирования функции f (x).
Свойства неопределённого интеграла Из определений первообразной F (x) и неопределённого интеграла от данной функции f (x) на некотором промежутке следуют свойства неопределённого интеграла: 1. 2. 3. 4. 5.
Замечание. Все вышеперечисленные свойства верны при условии, что интегралы, фигурирующие в них, рассматриваются на одном и том же промежутке и существуют.
Таблица основных неопределённых интегралов Действие интегрирования является обратным действию дифференцирования, т.е. по заданной производной функции f (x) надо восстановить начальную функцию F (x). Тогда из определения 2 и таблицы производных (см. §4, п. 3, с. 24) получается таблица основных интегралов. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. В формулах 1-16 С – произвольная постоянная. Замечание. Интеграл, взятый не от любой элементарной функции, является элементарной функцией. Примерами могут служить следующие интегралы, часто встречающиеся в задачах:
Указанные функции существуют и имеют важное прикладное значение. Для этих функций составлены таблицы значений.
МЕТОДЫ ИНТЕГРИРОВАНИЯ Непосредственное интегрирование а) Работа с таблицей: предложенный интеграл оказался одним из табличных интегралов. В этом случае требуется безошибочно найти соответствующую формулу таблицы основных интегралов и ею воспользоваться. Пример 1. 1. 2.
б) Метод разложения: предложенный интеграл после применения линейных свойств (4 и 5) неопределённого интеграла заменяется на алгебраическую сумму табличных интегралов. Пример 2.
Ответ: Пример 3.
Ответ: Пример 4.
Ответ: в) Подведение под знак дифференциала: предложенный интеграл удается свести к табличному с помощью изменения переменой интегрирования или за счёт преобразований под знаком дифференциала. При этом используют следующие формулы: d(j(x)) = j'(x)d x;
Далее используют тот факт, что если известен результат
то равенство
будет справедливо для любой дифференцируемой функции u = j(x). Пример 5.
Ответ:
Пример 6.
Ответ:
Пример 7.
Ответ: Пример 8.
Ответ: Пример 9.
Ответ:
Интегрирование подстановкой Подстановка (или замена переменной) базируется на следующей теореме. Теорема 1. Если не удаётся найти интеграл 1) j(t) непрерывна при t Î (a;b), соответствующем интервалу x Î (a; b), 2) дифференцируемая при t Î (a;b); 3) имеет обратную функцию t = j–1(x), чтобы
стал табличным или более простым. Иногда для упрощения интеграла можно сделать замену t = y(x). Замечание. Выбор правильной подстановки в значительной степени зависит от искусства вычисляющего.
Пример 10.
Ответ: Пример 11.
Ответ: Пример 12.
Ответ: Пример 13.
Ответ:
Интегрирование по частям Метод интегрирования по частям базируется на следующей теореме. Теорема 2. Пусть функции u = u (x) и v = v (x) дифференцируемы на некотором интервале (a; b). Пусть на интервале (a; b) функция v (x)× u '(x) имеет первообразную. Тогда на интервале (a; b) функция u (x)× v '(x) также имеет первообразную. При этом справедливо равенство:
Доказательство. По формуле дифференцирования произведения: (u (x)× v (x))'= u '(x)× v (x) + u (x)× v '(x) и свойству неопределённого интеграла:
можно записать:
Замечание 1. Определение дифференциала и свойства инвариантности его формы позволяют переписать формулу интегрирования по частям в более короткой форме:
Замечание 2. Для успешного вычисления интеграла необходимо разумно разбить подынтегральное выражение на два множителя u (x) и d v (x) так, чтобы интеграл Практика показывает, что большая часть интегралов, берущихся с помощью метода интегрирования по частям, может быть разбита на следующие три группы. 1)Кпервой группе относятся интегралы, у которых подынтегральная функция содержит в качестве множителя одну из следующих функций: ln x; arcsin x; arccos x; arctg x; arcctg x; ln2 x; lnj(x); arcsin2 x;… при условии, что оставшаяся часть подынтегральной функции представляет собой производную известной функции. Тогда за функцию u (x) берут соответствующую из перечисленных. 2) Ковторой группе относятся интегралы вида:
где a, b, a, n, A – некоторые постоянные числа, A > 0, n Î N.
При этом в качестве u (x) следует брать (ax + b) n и интегрировать по частям n раз. 3) К третьей группе относятся интегралы вида:
где a, b, A – постоянные числа, A > 0, A ≠ 1. Такие интегралы берутся двукратным интегрированием по частям при любом выборе u (x). Это приводит к линейному уравнению относительно предложенного интеграла, откуда его и находят. Замечание. Указанные три группы не исчерпывают всех без исключения интегралов, берущихся методом интегрирования по частям.
Пример 14.
Ответ: Пример 15.
Ответ: Пример 16.
Ответ: Пример 17.
Ответ: Пример 18.
Далее необходимо решить уравнение:
Ответ: Пример 19.
Пусть
Ответ:
|
||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 175; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.218.44 (0.009 с.) |

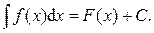
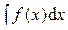 знак
знак 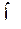 называется знаком интеграла,
называется знаком интеграла, 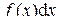 – подынтегральным выражением,
– подынтегральным выражением, 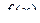 – подынтегральной функцией,
– подынтегральной функцией, 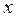 – переменной интегрирования.
– переменной интегрирования.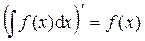 .
.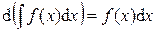 .
.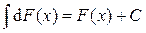 , где С – произвольная постоянная.
, где С – произвольная постоянная.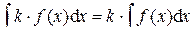 , где k = const.
, где k = const.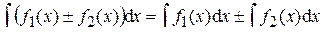
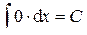 .
.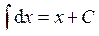 .
.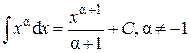 .
.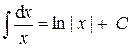 .
.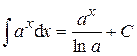 .
.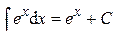 .
.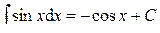 .
.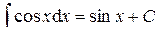 .
.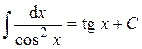 .
.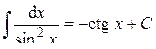 .
. .
.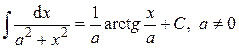 .
.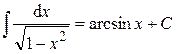 .
.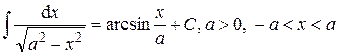 .
.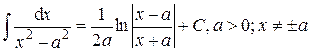 .
.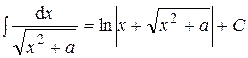 .
.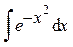 – интеграл Пуассона,
– интеграл Пуассона,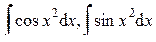 – интегралы Френеля,
– интегралы Френеля,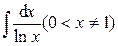 – интегральный логарифм,
– интегральный логарифм,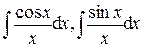
 – интегральный косинус и синус.
– интегральный косинус и синус.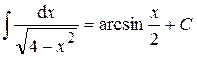 (формула 14)
(формула 14)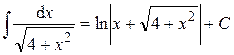 (формула 16)
(формула 16)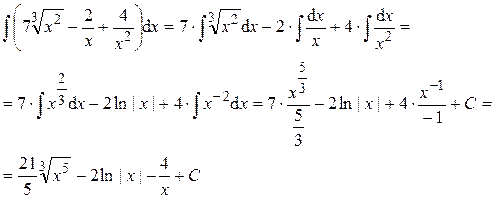
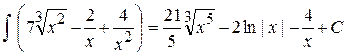 .
.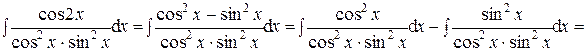
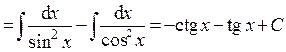
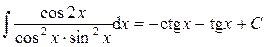 .
.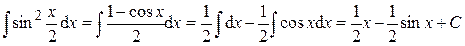
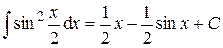
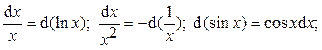
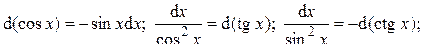
 и т.д.
и т.д.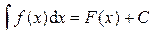 ,
,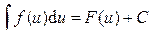
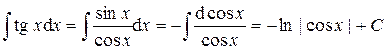
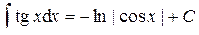 .
.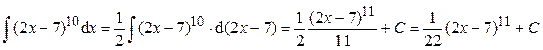 .
.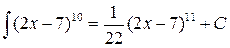 .
.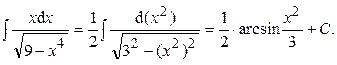
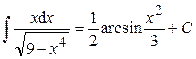 .
.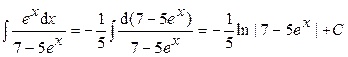 .
.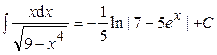 .
.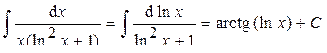 .
.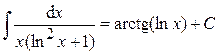 .
. непосредственно, то можно выбрать такую функцию x = j(t), удовлетворяющую условиям:
непосредственно, то можно выбрать такую функцию x = j(t), удовлетворяющую условиям: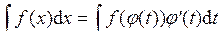 , t = j–1(x)
, t = j–1(x)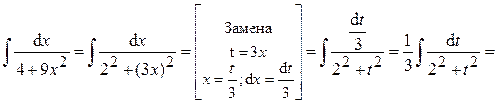
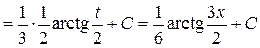 .
.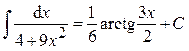 .
.
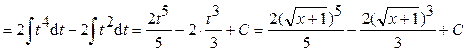 .
.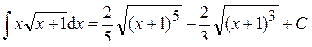 .
.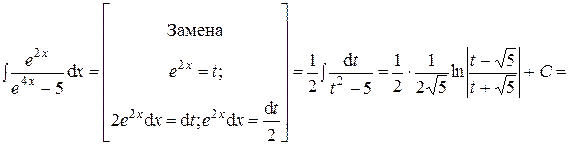
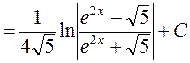 .
.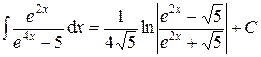 .
.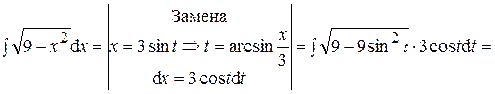
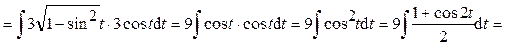
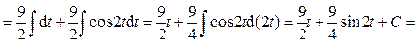
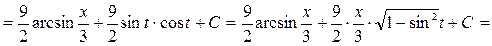
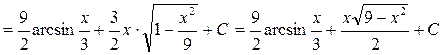 .
.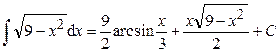 .
.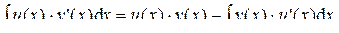 .
.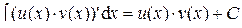
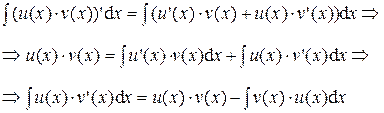
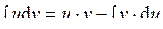 .
.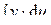 оказался легко интегрируемым.
оказался легко интегрируемым.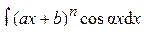 ,
, 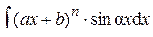 ,
,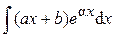 ,
, 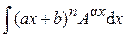 ,
,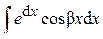 ,
, 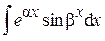 ,
, 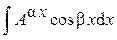 ,
,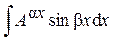 ,
, 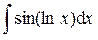 ,
, 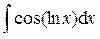 ,
,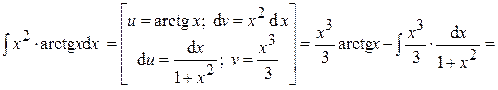
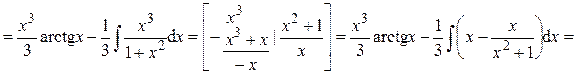
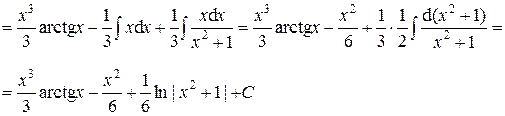
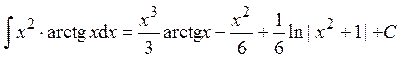
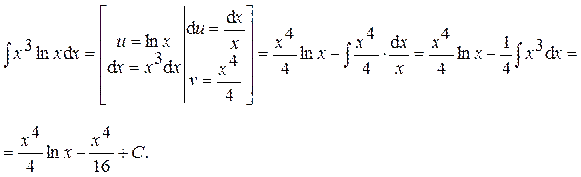
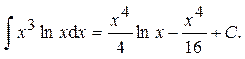
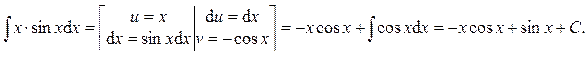
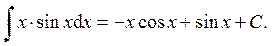
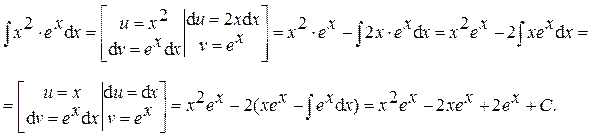
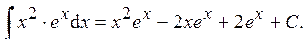
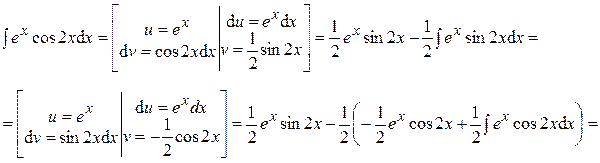
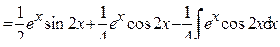

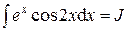 , тогда уравнение запишется в виде:
, тогда уравнение запишется в виде: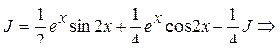
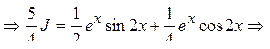
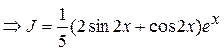 .
.
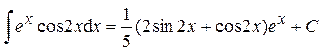 .
.
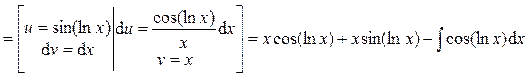 .
.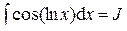 , тогда получаем уравнение вида:
, тогда получаем уравнение вида: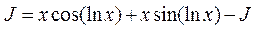
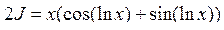
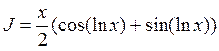 .
.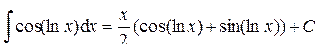 .
.


