
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные теоремы о конечных пределахСодержание книги
Поиск на нашем сайте
Теорема 1. Функция f (x) имеет конечный предел в точке Доказательство этой теоремы вытекает из определения предела функции в точке и определения бесконечно малой функции в точке. Теорема 2. Если существуют конечные пределы двух функций f (x) и g (x) в точке Доказательство: Пусть f (x) + g (x) = A + a(x) + B + β(x) = (A + B) + a(x) + β(x). Обозначим γ(x) = a(x)+ β(x) – бесконечно малая функция в точке x 0 ( по свойству 1 бесконечно малых функций). Получим f (x) + g (x)= A + B + γ(x). По теореме 1: Теорема доказана. Теорема 3. Если существуют конечные пределы двух функций f (x) и g (x) в точке Доказательство: Пусть f (x) × g (x) = (А +a(x))(B + β(x)) = A × B + B ×a(x) + A × β(x) +a(x) ×β(x). Обозначим: B ×a(x)+ A ×β(x) + a(x) ×β(x) = γ(x), где γ(x) – бесконечно малая функция в точке По теореме 1: Теорема доказана. Теорема 4. Если существуют конечные пределы f (x) и g (x), причём
Теорема 5 (о пределе трёх функций). Если существуют равные конечные пределы функций f (x) и g (x) в точке
и при стремлении x к x 0выполняется неравенство:
то существует Доказательство: Возьмем любое e > 0. Вычитая из всех частей двойного неравенства, данного в условии, число A, получим Так как
то найдётся такое d1, что для всех x ¹ x 0, удовлетворяющих условию
будет верно неравенство
или, что то же, Аналогично для функции g (x) найдётся такое d 2, что для всех x ¹ x 0, удовлетворяющих условию
будет верно неравенство Из неравенств, отмеченных (*), следует, что
или, что то же самое |φ(x) для всех x ¹ x 0, удовлетворяющих условию
Теорема доказана.
Первый замечательный предел Теорема 6. Предел функции Доказательство:
1) Пусть угол x > 0 (x
где угол х в радианах. Подставим в соотношение (1) полученные значения площадей:
Так как все части двойного неравенства положительные, выражение можно переписать так:
Так как
2) Пусть x < 0 (x
Теорема доказана.
Второй замечательный предел Теорема 7. Предел функции
Замечание. Число e является пределом последовательности
|
|||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 101; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.32.243 (0.01 с.) |

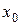 тогда и только тогда, когда выполняется равенство: f (x) = А +a(x), где a(x)– бесконечно малая функция в точке
тогда и только тогда, когда выполняется равенство: f (x) = А +a(x), где a(x)– бесконечно малая функция в точке 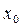 .
.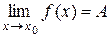 , тогда по теореме 1 f (x) = А +a(x), где a(x) – бесконечно малая функция в точке x 0. Пусть
, тогда по теореме 1 f (x) = А +a(x), где a(x) – бесконечно малая функция в точке x 0. Пусть 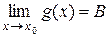 , тогда по теореме 1 g (x) = B + β(x), где β(x) – бесконечно малая функция в точке x 0. Рассмотрим сумму этих функций:
, тогда по теореме 1 g (x) = B + β(x), где β(x) – бесконечно малая функция в точке x 0. Рассмотрим сумму этих функций: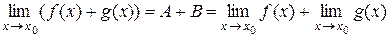 .
. . Пусть
. Пусть 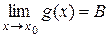 , тогда по теореме 1: g (x) = B + β(x), где β(x) – бесконечно малая функция в точке
, тогда по теореме 1: g (x) = B + β(x), где β(x) – бесконечно малая функция в точке 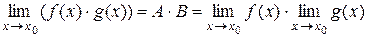 .
.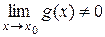 , то существует предел частного этих функций
, то существует предел частного этих функций 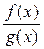 в точке
в точке 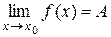 и существует
и существует 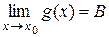 , B ≠ 0, то существует
, B ≠ 0, то существует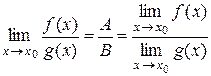 (доказать самостоятельно).
(доказать самостоятельно).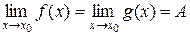
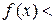 φ(x)
φ(x) 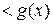
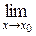 φ(x), равный А.
φ(x), равный А.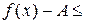 φ(x)
φ(x) 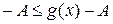 (*)
(*)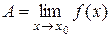 ,
,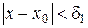 ,
,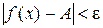 ,
,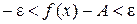 (*)
(*)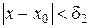 ,
,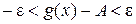 . (*)
. (*)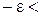 φ(x)
φ(x) 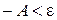 ,
,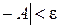
 , где d – меньшее из d1 и d2. Это означает, что
, где d – меньшее из d1 и d2. Это означает, что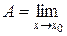 φ(x).
φ(x).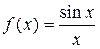 в точке
в точке 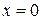 существует и равен 1, т.е.
существует и равен 1, т.е. 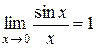 .
.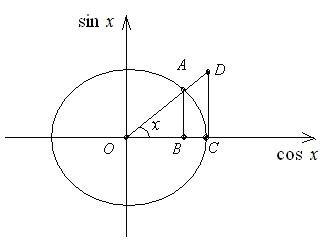
 ). Площади
). Площади  соотносятся:
соотносятся: (1)
(1) ;
; 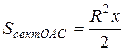 ;
; 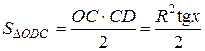 ,
,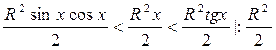 ,
,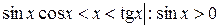 ,
,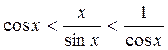
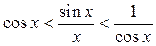
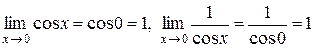 то по теореме 5:
то по теореме 5: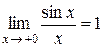 .
. )
)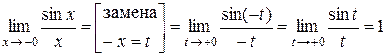 (по доказанному в первом случае). Следовательно,
(по доказанному в первом случае). Следовательно,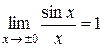 .
. при x
при x  существует и равен числу e, т.е.
существует и равен числу e, т.е.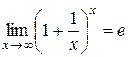 .
.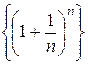 , причем это число иррациональное, т.е. представляется бесконечной непериодической десятичной дробью: e = 2,7182818284590…. Более того, число e трансцендентное, т.е. не является корнем алгебраического уравнения с целыми коэффициентами. В математическом анализе это число играет особую роль, в частности, является основанием натурального логарифма. Показательная функция с основанием e:
, причем это число иррациональное, т.е. представляется бесконечной непериодической десятичной дробью: e = 2,7182818284590…. Более того, число e трансцендентное, т.е. не является корнем алгебраического уравнения с целыми коэффициентами. В математическом анализе это число играет особую роль, в частности, является основанием натурального логарифма. Показательная функция с основанием e: 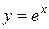 , называется экспонентой.
, называется экспонентой.


