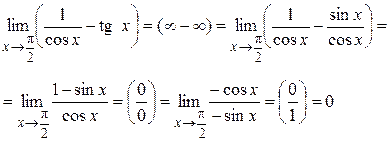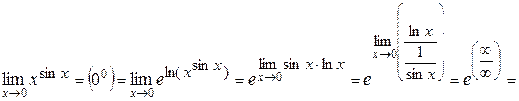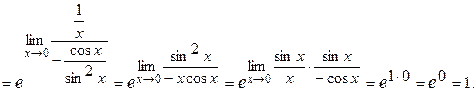Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрический смысл теоремы РолляСодержание книги
Поиск на нашем сайте
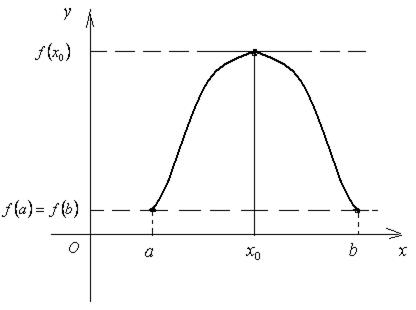
С геометрической точки зрения теорема Ролля означает, что график функции, непрерывной на отрезке [ a; b ], дифференцируемой на интервале (a; b) и принимающей на концах отрезка равные значения, имеет хотя бы одну точку с координатами (х 0 ; f (х 0)), где х 0Î (a; b), в которой касательная параллельна оси O x (рис. 7).
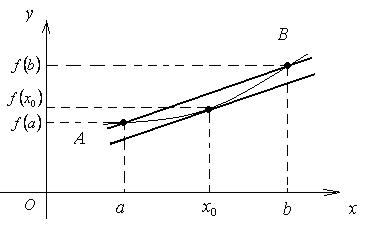
Рис. 7 Теорема Лагранжа Теорема 5 (теорема Лагранжа). Если функция f (x) определена на отрезке [ a; b ] и выполнены следующие условия: · f (x) непрерывна на отрезке [ a; b ], · f (x) дифференцируема на интервале (a; b), то внутри этого отрезка существует хотя бы одна точка х 0, в которой выполняется равенство: f ' (х 0) = Доказательство. Рассмотрим вспомогательную функцию F (x) = f (x) + l× x, где l = const. Потребуем, что бы для F (x) выполнялось условие F (a) = F (b). Так как F (a) = f (a) + l× a и F (b) = f (b) + l× b, то получим равенство: f (a) + l× a = f (b) + l× b. Отсюда выразим значение l: l = – При этом значении l функция F (x) = f (x) – Функция F (x) удовлетворяет всем условиям теоремы Ролля: · F (x) непрерывна на отрезке [ a; b ]: · F (x) дифференцируема на интервале (a; b) · F (a) = F (b). Следовательно, по теореме Ролля на интервале (a; b) существует хотя бы одна точка х 0, в которой выполняется равенство: F '(х 0) = 0. Найдём F '(x): F '(x) = f '(x) – Поэтому F '(x 0) = f '(х 0) – Теорема доказана. Геометрический смысл теоремы Лагранжа С геометрической точки зрения теорема Лагранжа означает, что график функции, непрерывной на отрезке [ a; b ] и дифференцируемой на интервале (a; b), имеет хотя бы одну точку (х 0; f (х 0), в которой касательная параллельна секущей, проходящей через точки A (a; f (a)) и B (b; f (b)) (рис. 8)
Рис. 8 Теорема Коши Теорема 6 (теорема Коши). Если функции f (x) и g (x) определены на отрезке [ a; b ] и удовлетворяют условиям: · f (x) и g (x) непрерывны на отрезке [ a; b ]; · f (x) и g (x) дифференцируемы на интервале (a; b); · g '(x) ¹ 0 при любом x Î (a; b), то внутри отрезка [ a; b ] найдётся хотя бы одна точка х 0, в которой выполняется равенство:
Доказательство аналогично доказательству теоремы 5 (теорема Лагранжа) при вспомогательной функции F (x) = f (x) + l × g (x), где l = const, которую выбирают так, чтобы F (a) = F (b). Правило Лопиталя Теорема 7 (правило Лопиталя). Если функции f (x) и g (x) определены в некоторой окрестности точки х 0 и в этой окрестности они удовлетворяют условиям:
· f (x) и g (x) дифференцируемы в каждой точке за исключением может быть самой точки х 0; · g '(x) ¹ 0 для любого x из этой окрестности; · тогда, если существует
Замечание 1. Правило Лопиталя используется для раскрытия неопределённостей типа Замечание 2. Если к условиям теоремы 7 добавить дифференцируемость функций f '(x) и g '(x) в окрестности точки х 0, то при выполнении остальных требований для f '(x) и g '(x) правило Лопиталя можно применить повторно. При этом будет справедливо равенство:
Пример 1. Вычислить предел:
Пример 2. Вычислить предел:
Пример 3. Вычислить предел:
Пример 4. Вычислить предел:
Пример 5. Вычислить предел:
Пример 6. Вычислить предел:
|
|||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 204; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.138.214 (0.009 с.) |

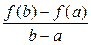 .
.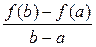 .
.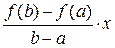 .
.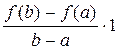 .
.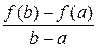 = 0, если f '(х 0) =
= 0, если f '(х 0) = 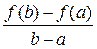 .
.
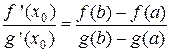 .
.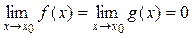 или
или 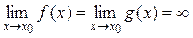 ,
,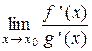 конечный или бесконечный, то выполняется равенство:
конечный или бесконечный, то выполняется равенство: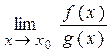 =
= 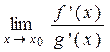 .
.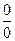 или
или 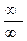 , возникающих при вычислении пределов. Если под знаком предела оказывается неопределённость другого типа: 0×∞,
, возникающих при вычислении пределов. Если под знаком предела оказывается неопределённость другого типа: 0×∞, 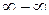 , 10, 00 или ∞0, то с помощью тождественных алгебраических преобразований такая неопределённость приводится к
, 10, 00 или ∞0, то с помощью тождественных алгебраических преобразований такая неопределённость приводится к 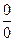 или
или 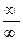 и тогда можно применить правило Лопиталя.
и тогда можно применить правило Лопиталя.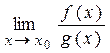 =
= 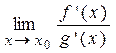 =
= 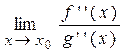
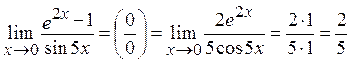
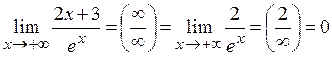
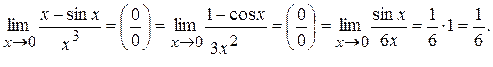
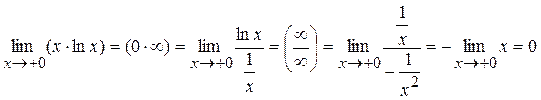 .
.