Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функции сложных процентов. ДисконтированиеСодержание книги
Поиск на нашем сайте
Принципиальное значение для процедур оценки изменения стоимости денег во времени имеет также различие в сути простых и сложных процентов. Рассмотрим это различие на примере наращения банковского вклада в сумме 1000 рублей, размещенного под 10% годовых. Простой процент – доход исчисляются только от первоначальной основной суммы. Таблица 2.1.
Сложный процент – полученный доход присоединяется к основной сумме вклада и в последующем платежном интервале сам приносит доход.
Таблица 2.2.
Сложный процент, как уже указывалось, используют при исчислении дохода от долгосрочных операций. Система базовых понятий позволяет рассмотреть методический инструментарий оценки стоимости денег во времени применительно к наиболее частым вариантам выполнения такой оценки в практике инвестиционной и риелтерской деятельности с использованием сложных процентов при обычном (декурсивном) способе начисления процента. Введем обозначения: PV – настоящая стоимость; FV – будущая стоимость; N - число лет в периоде начисления; k - число интервалов в течение года; n - общее число интервалов начисления в течение периода начисления (n=N J - годовая номинальная процентная ставка, выражается в долях единицы; i - периодическая процентная ставка (i = J: k); Jэ – годовая эффективная процентная ставка Jэ = Рассмотрим варианты оценки стоимости денег во времени с использованием сложных процентов[3]. 1. Расчет будущей стоимости капитала (вклада) Будущая стоимость капитала, инвестированного или депонированного на определенное число лет, с учетом накопления процентов определяется по формуле
FV = PV (1+J)N. (2.1) Будущую стоимость в этом варианте называют еще аккумулированная сумма капитала. Когда начисление сложных процентов осуществляется не один, а несколько раз в году, то расчет выполняется по формуле
FV = PV (1+i)n. (2.2.) Множитель (коэффициент) наращения аккумулированной суммы капитала выражается как m1=(1+i)n. Он характеризует будущую стоимость единицы и выступает в качестве базисного элемента во всех последующих расчетных формулах. Задача 2.1. Вклад в сумме 1000 руб. размещен на 1 год под 10% годовых. Проценты начисляются ежеквартально. Необходимо определить: периодическую ставку процента, будущую стоимость вклада, доход на капитал (Д) и годовую эффективную ставку процента. Формализация задачи: PV=1000 руб.; J=0,1; k=4.
i=? FV=? Д=? Jэ=? Решение: 1. i=0,10:4=0,025 2. FV=PV =1000 3. Доход=1103,8-1000=103,8 руб.
4. Jэ= Вывод: годовая эффективная ставка выше годовой номинальной; ее величина с увеличением числа интервалов начислений возрастает.
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-28; просмотров: 75; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.117.125 (0.011 с.) |

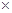 k);
k);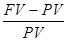 .
.