
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные сведения о статической моделиСодержание книги
Поиск на нашем сайте
Статистические модели используются при различных уровнях текущего планирования от народного хозяйства в целом до отдельного предприятия. Эти модели представляет собой систему линейных алгебраических равенств
где
В матричной форме система (11.1) имеет вид
где
Модель (11.2) позволяет по заданному вектору X определять вектор Y. Если существует обратная матрица
Матрица Важной характеристикой балансовой системы является продуктивность матрицы А. Матрица А называется продуктивной, если любому
Коэффициенты полных затрат определяются по известным коэффициентам прямых затрат на основе использования следующих соотношений: а) где
б) приближенный способ, используемый только для продуктивной матрицы A
в) обращения матрицы
Если Полагая в системе (11.6) неизвестными элементы матрицы S, получаем уравнения, используемые для их определения. Пример 11.1. Для экономической системы, состоящей из трех отраслей, связанных взаимными поставками, известны максимально возможные отраслевые валовые выпуски
Коэффициенты прямых затрат составляют
Определить: а) продуктивность матрицы А; б) объем конечного продукта по отраслям. Решение а) Используя соотношение (11.4) устанавливаем, является ли матрица А продуктивной
Условие (11.4) выполняется, следовательно матрица А − продуктивная. б) Для определения объема конечного продукта по отраслям необходимо воспользоваться уравнениями системы (11.1)
Так как Задача 11.1. Для системы, состоящей из трех отраслей со значениями коэффициентов прямых затрат, приведенными в примере 11.1, определить по заданному вектору конечного выпуска а) отраслевые валовые объемы; б) объемы межотраслевых поставок Задача 11.2. Имеется двухотраслевая балансовая система с матрицей прямых затрат
Отраслевые производственные возможности составляют а) максимально возможный конечный выпуск при соблюдении пропорции б) величину неиспользованных производственных возможностей при заданной структуре конечного потребления. Задача 11.3. Для значений коэффициентов прямых затрат из примера 11.1 определить коэффициенты полных затрат.
|
||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 125; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.74.47 (0.007 с.) |

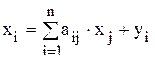 ,
, 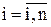 , (11.1)
, (11.1)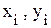 - валовой и конечный объемы продукта i-го вида (отрасли), руб.;
- валовой и конечный объемы продукта i-го вида (отрасли), руб.; - коэффициент прямых затрат продукции i-го вида, руб./руб.
- коэффициент прямых затрат продукции i-го вида, руб./руб.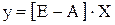 , (11.2)
, (11.2)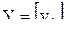 ,
, 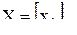 - векторы конечного и валового объема;
- векторы конечного и валового объема;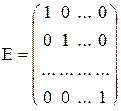 - единичная матрица;
- единичная матрица;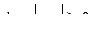 - матрица коэффициентов прямых затрат.
- матрица коэффициентов прямых затрат. , возможно решение обратной задачи нахождения вектора валового объема производства X, необходимого для выпуска конечного продукта, заданного вектором Y
, возможно решение обратной задачи нахождения вектора валового объема производства X, необходимого для выпуска конечного продукта, заданного вектором Y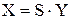 . (11.3)
. (11.3)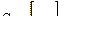 получила название матрицы коэффициентов полных затрат. Коэффициент
получила название матрицы коэффициентов полных затрат. Коэффициент 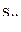 полных затрат численно равен валовому объему продукции i-гo вида, необходимому для производства единицы конечного продукта j-гo вида.
полных затрат численно равен валовому объему продукции i-гo вида, необходимому для производства единицы конечного продукта j-гo вида. соответствует
соответствует 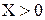 . Обратное утверждение не всегда верно. При некоторых
. Обратное утверждение не всегда верно. При некоторых 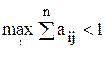 . (11.4)
. (11.4)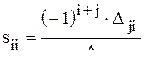 , (11.5)
, (11.5)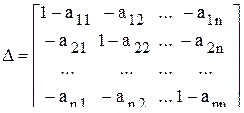 - главный определитель матрицы
- главный определитель матрицы  системы (11.2);
системы (11.2);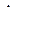 - определитель, получаемый из главного определителя
- определитель, получаемый из главного определителя 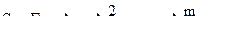 ;
; . (11.6)
. (11.6)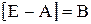 , где
, где 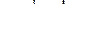 , то
, то 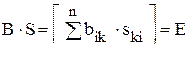 .
. ;
;  ;
; 
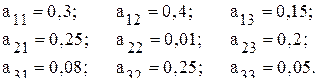
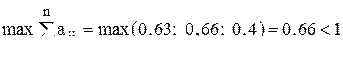 .
. млн.руб.;
млн.руб.; млн.руб.;
млн.руб.; млн.руб.
млн.руб.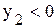 , для поддержания запланированных объемов производства необходимы поставки в систему из забалансового источника продукции второй отрасли на 0,355 млн.руб.
, для поддержания запланированных объемов производства необходимы поставки в систему из забалансового источника продукции второй отрасли на 0,355 млн.руб.
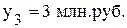 :
: .
.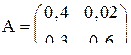 .
.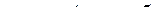 ;
; 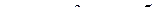 Определить:
Определить: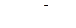 ;
;


