
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модели оперативного управления балансовыми пропорциямиСодержание книги
Поиск на нашем сайте
В отличие от планирования межотраслевых связей задача оперативного управления этими связями приобретает содержательный смысл в условиях несовершенной информационной базы расчетов, что приводит к нарушению ожидаемых пропорций. Так в статической модели источники погрешностей − неточное определение коэффициентов прямых затрат или использование приближенных методов обращения матрицы Идея управления заключается в периодической корректировке отраслевых валовых объемов в зависимости от разницы между заданным и фактическим объемами выпуска конечной продукции (ошибки) в плановом периоде нарастающим итогом. Таким образом, реализуется принцип управления "по отклонению" регулируемой величины от плановой траектории конечного выпуска. Пусть
где
Тогда отклонение интенсивности в
где
Процесс управления считается устойчивым, если
Условие (13.3) выполняется, если
Из общего критерия (13.4) можно получить ряд частных критериев. Например, полагая
Известно, что Поэтому вместо (13.5) можно использовать более жесткий критерий
или
Требование устойчивости − главное, но не единственное в теории управления. Следующим требованием является приемлемая точность, качество управления. Для экономических процессов важнейшими показателями качества являются текущие отклонения от плановой траектории и итоговые отклонения от плана. В терминологии системной динамики − это накопившаяся ошибка за Т циклов и установившаяся ошибка (если число циклов достаточно велико). Соответственно расчетные формулы при
где Пример 13.1. Имеется система из двух отраслей с матрицей плановых коэффициентов
и матрицей отклонений от плановых коэффициентов
Плановый годовой объем выпуска конечной продукции Длительность цикла управления − один месяц. Требуется: 1. Проверить сходимость процесса управления; 2. Вычислить для нескольких начальных циклов последовательность фактических интенсивностей Решение По матрице A предварительно определяются плановые коэффициенты полных затрат
В соответствии с критериями (8.6)
Таким образом, наиболее жесткий критерий свидетельствует о том, что отклонения удельных затрат от плановых норм недопустимо велики, и процесс неустойчив. Далее используется уточненный критерий. Пусть Тогда
Определяем элементы матрицы
В соответствии с (13.5) находим
Поскольку одна из норм матрицы C меньше единицы, процесс сходится. Если бы уточненный достаточный критерий не гарантировал сходимости, ее следовало бы определить непосредственным вычислением характеристических чисел матрицы С. В данном примере они равны 0,4293685 и -0,2451579. Далее определяется матрица фактических коэффициентов прямых затрат
1-й цикл Плановые объемы производства
Фактические объемы конечного выпуска
Отклонение от плановых объемов конечного выпуска
Й цикл Задание по конечному выпуску
Плановые объемы производства
Фактические объемы конечного выпуска
Отклонение от плановых объемов конечного выпуска
Й цикл Задание по конечному выпуску
Плановые объемы производства
Фактические объемы конечного выпуска
Отклонение от плановых объемов конечного выпуска
Параметры остальных циклов вычисляются аналогично. Результаты расчетов для следующих трех циклов представлены в табл. 13.1. Таблица 13.1
Годовой план конечного выпуска выполнен: а) для первого продукта на
б) для второго продукта на
За единицу времени в примере принят месяц. Если бы оперативное управление отсутствовало, т.е.
Наоборот, при сокращении цикла управления до 0,5 месяца уменьшается отклонение от плана
Выполнение плана для первого и второго продуктов составляет соответственно 96 и 102,9 %. Определяем элементы матрицы
В соответствии с (8.5) находим
Поскольку одна из норм матрицы C меньше единицы, процесс сходится. Задача 13.1. Выявить устойчивость управления для системы с параметрами примера 13.1 с помощью критериев (13.3). Определить максимально допустимые величины погрешностей Задача 13.2. В системе с матрицей A из предыдущего примера
Определить устойчивость процесса управления (13.2), приняв Задача 13.3. В системе с параметрами примера 13.1 определить периодичность управляющих воздействий
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 107; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.209.231 (0.006 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||

 .
.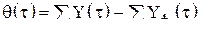 , (13.1)
, (13.1)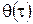 - вектор ошибки за
- вектор ошибки за 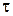 циклов;
циклов;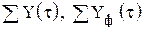 - векторы планового и фактического конечного выпусков за
- векторы планового и фактического конечного выпусков за 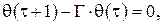 (13.2)
(13.2)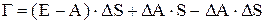 ;
; - матрицы погрешностей в определении соответствующих "плановых" коэффициентов
- матрицы погрешностей в определении соответствующих "плановых" коэффициентов 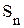 .
.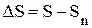 ;
; 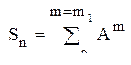 .
.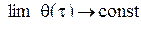 . (13.3)
. (13.3)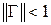 . (13.4)
. (13.4)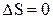 , получим
, получим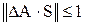 . (13.5)
. (13.5)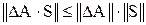 .
.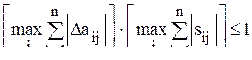 , (13.6)
, (13.6)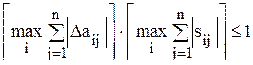 . (13.7)
. (13.7)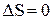 следующие
следующие , (13.8)
, (13.8)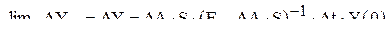 , (13.9)
, (13.9)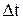 - длительность цикла управления.
- длительность цикла управления.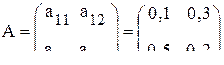
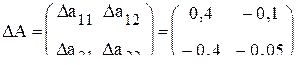 .
.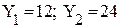 .
. , отклонений
, отклонений 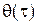 и оценить суммарное отклонение от планового годового объема конечного продукта.
и оценить суммарное отклонение от планового годового объема конечного продукта.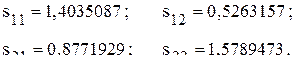
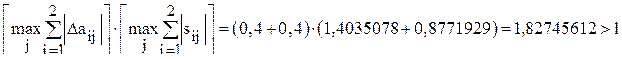 ,
,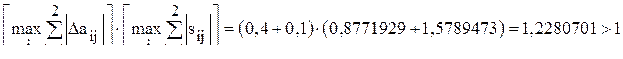 .
.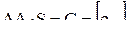
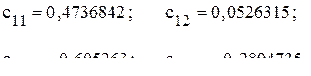
 ,
,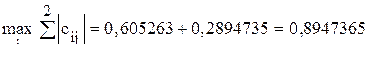 .
.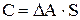
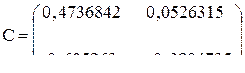 .
.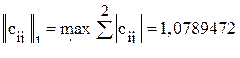 ;
;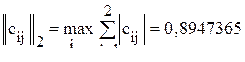 .
.
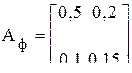 .
.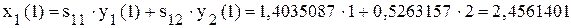 ;
;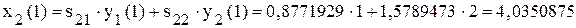 .
.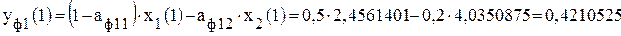 ;
;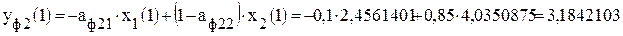 .
.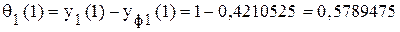 ;
;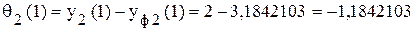 .
.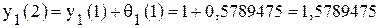 ;
;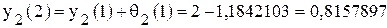 .
.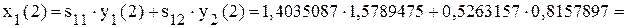
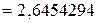 ;
;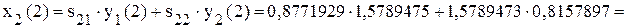
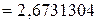 .
.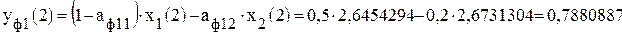 ;
;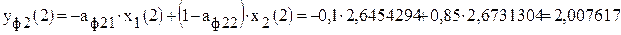 .
.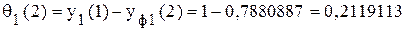 ;
;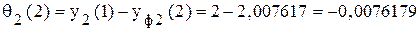 .
.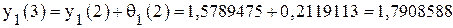 ;
;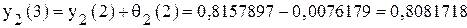 .
.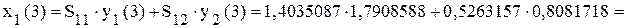
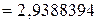 ;
;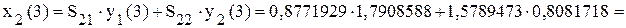
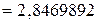 .
.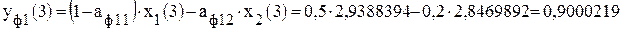 ;
;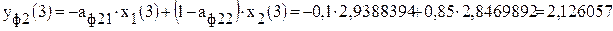 .
.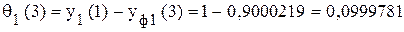 ;
;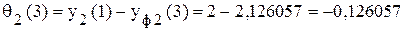 .
.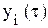
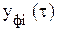
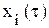
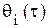
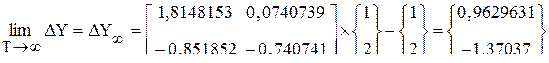 .
.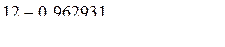 ;
; .
.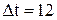 , то при имеющихся отклонениях от плановых норм
, то при имеющихся отклонениях от плановых норм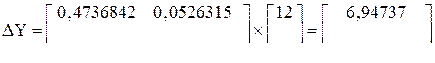 .
.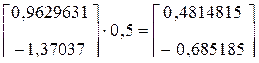 .
.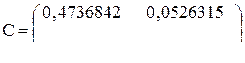 .
.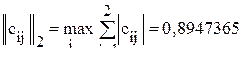 .
.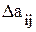 , при которых устойчивость еще сохраняется.
, при которых устойчивость еще сохраняется.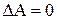 , а матрица S вычисляется разложением в ряд
, а матрица S вычисляется разложением в ряд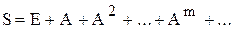 .
.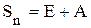 ,
, 


