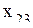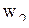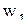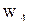Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача оптимального распределения производственной программы по календарным периодамСодержание книги
Поиск на нашем сайте
Одной из основных задач экономики предприятия является оптимальное распределение производственной программы по календарным периодам. Ее решение рассмотрим на примере 7.1. Пример 7.1. В механическом цехе машиностроительного предприятия в течение квартала должны быть обработаны три вида деталей. Количество деталей вида A – 400 шт., вида B – 300 шт. Для обработки деталей цех располагает двумя группами оборудования. Трудоемкость обработки единицы каждого вида деталей и месячные фонды времени работы оборудования каждой группы представлены в табл. 7.1. Таблица 7.1
Требуется распределить производство трех видов деталей по месяцам квартала, при котором обеспечивалась бы максимальная загрузка оборудования. Решение Распределение производственной программы по календарным периодам будет считаться оптимальным, если обеспечивается максимальная загрузка оборудования или недогрузка оборудования минимальная. Данную задачу следует решать отдельно для каждого месяца. Целевая функция, характеризующая величину недогруженности оборудования, определяется по формуле
где
Для января целевая функция будет иметь вид
На целевую функцию накладываются следующие ограничения: - ограничения по ресурсам
- ограничения по ассортименту
где Величина
где Для января ограничения по ассортименту будут следующие
Математическая постановка задачи для января приводится к виду, удобному для заполнения первой симплекс-таблицы. Для этого от ограничений-неравенств переходят к ограничениям-равенствам путем введения дополнительных переменных
Начальное допустимое базисное решение имеет следующий вид
Базисные переменные необходимо выразить через свободные и устремить целевую функцию к максимуму
Решение задачи представлено в табл. 7.2 - 7.4. Таблица 7.2
Таблица 7.3
Таблица 7.4
В табл. 7.4 получено оптимальное решение задачи для января. Для того чтобы свести недогрузку оборудования в январе к минимуму (к нулю), необходимо обработать 100 деталей вида A и 300 деталей вида C, при этом программа (квартальная) по деталям вида C будет полностью выполнена и в дальнейшем решении задачи детали вида C рассматриваться не будут. Математическая постановка задачи для определения производственной программы в феврале будет иметь следующий вид: - целевая функция
- ограничения по ресурсам
- ограничения по ассортименту
Математическую постановку задачи необходимо привести к виду, удобному для заполнения первой симплекс-таблицы (табл. 7.5). Таблица 7.5
Далее строится вторая симплекс-таблица (табл. 7.6). Таблица 7.6
Эта симплекс-таблица содержит оптимальное решение. Для того чтобы свести недогрузку оборудования в феврале к минимуму (140 ст.-ч недогрузка оборудования группы I), необходимо обработать 290 деталей вида А. Математическая постановка задачи для определения производственной программы в марте будет иметь следующий вид: - целевая функция
- ограничения по ресурсам
- ограничения по ассортименту
Математическую постановку задачи необходимо привести к виду, удобному для заполнения первой симплекс-таблицы (табл. 7.7). Таблица 7.7
Дальнейшее решение содержится в табл. 7.8 и 7.9. Таблица 7.8
Таблица 7.9
В табл. 7.9 получено оптимальное решение. В марте будут обработаны все оставшиеся детали, а именно: 10 деталей вида А и 600 деталей вида В, при этом оборудование группы II будет полностью загружено, а недогрузка оборудования группы I составит 280 ст.-ч. Таким образом, оптимальное распределение производства трех видов деталей по месяцам первого квартала представлено в табл. 7.10. Таблица 7.10
Задача 7.1. Машиностроительное предприятие в течение квартала выпускает три вида изделий. Квартальная программа по каждому виду изделий составляет соответственно 400, 200 и 300 шт. На каждое изделие расходуются материалы трех видов. Нормы расхода материалов и их запасы на начало каждого месяца приведены в табл. 7.11. Таблица 7.11
Необходимо составить производственную программу таким образом, чтобы величина остатков оборотных средств на конец каждого месяца была бы минимальной (остатки сырья после каждого месяца в дальнейших расчетах не учитывать). Задача 7.2. Машиностроительное предприятие в течение квартала выпускает три вида изделий. Квартальная программа по каждому виду изделий составляет соответственно 350, 280 и 200 шт. Каждое изделие проходит обработку на трех операциях. Трудоемкость обработки единицы каждого вида изделия и месячные фонды времени работы оборудования на каждой операции представлены в табл. 7.12. Таблица 7.12
Необходимо определить оптимальный план производства трех видов изделий, при этом выпуск изделия C в январе должен составлять 100 шт., а изделия A – не более 120 шт. Задача 7.3. Машиностроительное предприятие в течение квартала выпускает четыре вида изделий. Квартальная программа по каждому виду изделий составляет соответственно 210, 300, 120 и 350 шт. Каждое изделие проходит обработку на двух операциях. Трудоемкость обработки каждого вида изделий и месячные фонды времени работы оборудования на каждой операции представлены в табл. 7.13. Таблица 7.13
Необходимо определить оптимальный план производства четырех видов изделий, при этом выпуск изделий B в январе должен составить 100 шт., а изделий D – не менее 50 шт. ТРАНСПОРТНАЯ ЗАДАЧА
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 152; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.0.20 (0.007 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

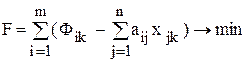 ,
,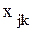 - количество деталей j-го вида, выпускаемых в k-м месяце;
- количество деталей j-го вида, выпускаемых в k-м месяце;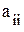 - трудоемкость обработки детали j-го вида на оборудовании i-й группы;
- трудоемкость обработки детали j-го вида на оборудовании i-й группы;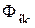 - фонд времени работы оборудования i-й группы в k-м месяце;
- фонд времени работы оборудования i-й группы в k-м месяце;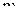 - количество групп технологического оборудования, на которых обрабатываются детали;
- количество групп технологического оборудования, на которых обрабатываются детали; - количество обрабатываемых деталей.
- количество обрабатываемых деталей.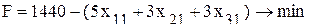 .
.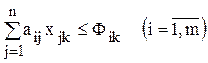 ;
;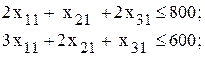
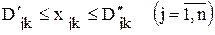 ,
,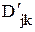 ,
, 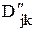 - наименьшее и наибольшее возможное количество изделий j-го вида, выпускаемых в k-м месяце.
- наименьшее и наибольшее возможное количество изделий j-го вида, выпускаемых в k-м месяце.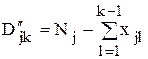 ,
,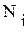 - программа выпуска изделий j-го вида за рассматриваемый период.
- программа выпуска изделий j-го вида за рассматриваемый период.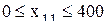 ;
;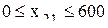 ;
;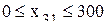 .
.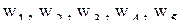
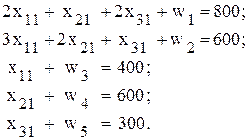
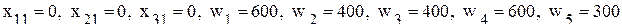 .
.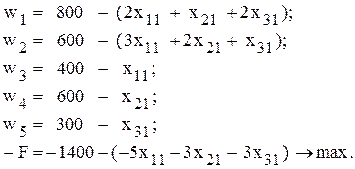
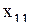 ↑
↑
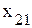
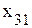
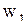
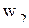
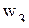
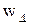
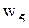
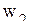
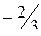
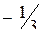
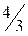
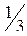
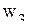
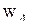
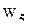
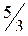
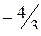

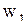
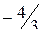
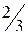
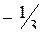
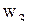
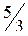
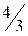
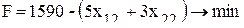 ;
;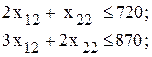
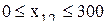 ;
; .
.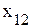 ↑
↑
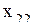

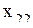
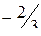
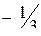
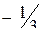
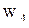
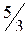
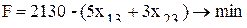 ;
;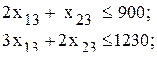
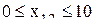 ;
;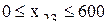 .
. ↑
↑