
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графический метод решения задачи линейногоСодержание книги
Поиск на нашем сайте
Программирования
Простейшим методом решения задачи линейного программирования является графический. Графический метод используется для получения решения задач, в которых участвуют в рассмотрении только две переменные. Графический метод решения задачи линейного программирования предусматривает осуществление следующих этапов: 1. Строится многоугольная область допустимых решений. 2. Строится вектор-градиент целевой функции. 3. Линия уровня При минимизации целевой функции линия уровня перемещается в направлении, противоположном вектору-градиенту. Если прямая при своем движении не покидает области допустимых решений, то соответствующий максимум или минимум целевой функциине существует. Использование графического метода для решения задач линейного программирования рассмотрим на примере 2.1. Пример 2.1. Определить оптимальный план производства двух видов изделий А и Б для машиностроительного предприятия, максимизирующий прибыль, при ограниченном объеме используемых материальных ресурсов. Данные о нормах расхода используемых ресурсов и прибыли на единицу изделия приведены в табл. 2.1. Таблица 2.1
Решение Этап 1. Математическая постановка задачи. Пусть
при ограничениях
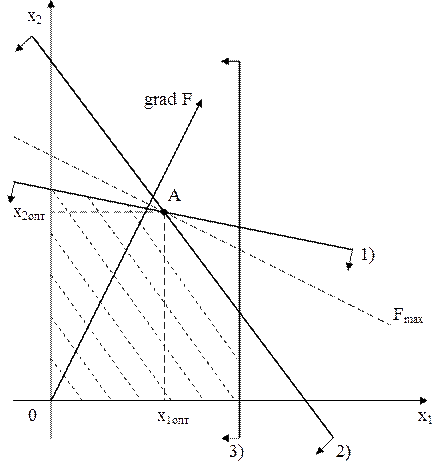
Этап 2. Графическое решение задачи. На плоскости построим декартову систему координат (рис. 2.1). На горизонтальной оси наносим значения переменной 1) 2) 3) 4) 5)
Рис. 2.1. Графическое решение задачи определения оптимального плана производства двух видов изделий Пять полуплоскостей образуют область определения целевой функции, которая называется областью допустимых решений (область ОДР, заштрихована). Задача заключается в том, чтобы из всех точек области ОДР найти такую, в которой целевая функция принимает максимальное значение. Известно, что если целевая функция имеет экстремум в ОДР, то он обычно достигается в вершине ОДР. Для рассматриваемой задачи многоугольник, образующий ОДР, имеет пять вершин. Для выбора вершины, дающей максимум целевой функции, необходимо построить градиент. Градиент – это радиус-вектор, выходящий из начала координат и показывающий направление наискорейшего роста функции. Для построения градиента необходимы две точки, одной из которых будет начало координат, а другую определим по формуле:
где Тогда
т. е. вторая точка будет иметь координаты (2, 4). Построив градиент (рис. 2.1), легко можно определить единственную точку, дающую максимум целевой функции. Эта точка А с координатами (3, 5). Таким образом, целевая функция достигает максимума при
Этап 3. Анализ полученного результата. Оптимальным планом производства для машиностроительного предприятия будет выпуск изделия А в количестве 3 шт. и изделия Б – 5 шт., при этом предприятие получит максимальную прибыль в размере 26 тыс.руб. Задача 2.1. Изготовление двух видов изделий А и Б включает выполнение четырех операций. Трудоемкость обработки каждого изделия на этих операциях, фонды времени и прибыль на единицу изделия приведены в табл. 2.2. Таблица 2.2
Определить, сколько изделий каждого вида необходимо выпустить для получения максимальной прибыли. Задача 2.2. Определить оптимальный план производства двух видов изделий А и Б для получения предприятием максимальной прибыли. Исходные данные приведены в табл. 2.3. Таблица 2.3
Задача 2.3. В литейном производстве для получения сплава требуемого химического состава и качества вводятся в жидкий металл четыре элемента. Например, на 1 т жидкого металла требуется 6 ед. элемента А, 12 ед. элемента Б, 4 ед. элемента В и 9 ед. элемента Г. В качестве добавок используются два вещества. Первое вещество стоимостью 5 усл.ед. за 1 кг содержит в 1 кг 2 ед. элемента А, 2 ед. элемента Б, 6 ед. элемента Г. Второе вещество стоимостью 6 усл. ед. за 1 кг содержит в 1 кг 1 ед. элемента А, 4 ед. элемента Б, 4 ед. элемента В. Требуется установить, в какой пропорции и в каком количестве необходимо взять оба вещества с тем, чтобы было достигнуто требуемое содержание каждого из элементов при минимальных затратах на приобретение обоих веществ.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 181; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.36.215 (0.006 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

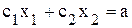 (где
(где 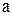 - постоянная величина) − прямая, перпендикулярная вектору-градиенту — передвигается в направлении этого вектора в случае максимизации целевой функциидо тех пор, пока не покинет пределов области допустимых решений. Предельная точка (или точки) области допустимых решений при этом движении и является точкой максимума целевой функции.
- постоянная величина) − прямая, перпендикулярная вектору-градиенту — передвигается в направлении этого вектора в случае максимизации целевой функциидо тех пор, пока не покинет пределов области допустимых решений. Предельная точка (или точки) области допустимых решений при этом движении и является точкой максимума целевой функции.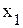 – количество выпускаемых изделий вида А;
– количество выпускаемых изделий вида А; 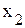 – количество выпускаемых изделий вида Б. Тогда целевая функция примет вид
– количество выпускаемых изделий вида Б. Тогда целевая функция примет вид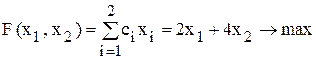
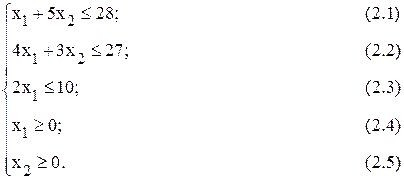
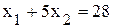 ;
;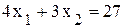 ;
;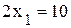 ;
;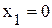 ;
;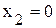 .
.
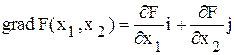 ,
,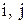 - радиус-векторы, совпадающие с координатными осями
- радиус-векторы, совпадающие с координатными осями 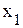 и
и 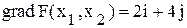 ,
,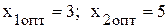 .
.


