
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование динамических процессовСодержание книги
Поиск на нашем сайте
Основные положения моделирования динамических процессов
Моделирование динамических процессов позволяет проследить изменение во времени наиболее существенных параметров экономической системы с целью их регулирования. Например, процесс расширенного воспроизводства при агрегированном представлении параметров имеет структуру, представленную на рис. 10.1.
Рис. 10.1. Структура модели расширенного воспроизводства: y(t) - текущий объем (интенсивность) выпуска конечного продукта; g(t) - интенсивность капитальных вложений в расширение основных фондов (инвестиции); c(t) - интенсивность непроизводственного потребления; x(t), l(t) - текущие объемы предметов труда и живого труда; r(t) - объем основных производственных фондов; tк - среднее время запаздывания в освоении основных производственных фондов; k - усредненный коэффициент приростной фондоемкости, численно равный приращению объема валового продукта на 1 рубль капиталовложений; F - производственная функция При
где
Решение дифференциального уравнения (10.1) имеет вид
Если
Решение дифференциального уравнения (5.3) имеет вид
где
Если
Если
Характер процесса воспроизводства определяется параметрами системы: a) b) Пример 10.1. Показать, что в модели без запаздывания в освоении капиталовложений Решение Чтобы найти условия расширенного воспроизводства, достаточно показать, что функция (5.2) монотонно возрастает, то есть Действительно,
Пример 10.2. Решить уравнение процесса воспроизводства при следующих значениях параметров: Решение Используя соотношение (10.5):
определяют корни
В результате решения системы двух уравнений
рассчитываются величины Так как корни вещественные, интенсивность конечного выпуска определяется по формуле (10.7):
Задача 10.1. Исследовать процесс изменения интенсивности выпуска конечного продукта в системе без запаздывания и построить график. Как влияет на изменение интенсивности конечного продукта начальное состояние экономики у(0) и уровень непроизводственного потребления Задача 10.2. Для модели без запаздывания задано: Задача 10.3. Построить кривую зависимости параметров Задача 10.4. Показать, что при любых вещественных корнях характеристическое уравнения (10.5) обеспечивается расширенное воспроизводство конечного продукта.
|
||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 200; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.166.207 (0.006 с.) |


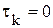 процесс расширенного воспроизводства описывается дифференциальным уравнением вида
процесс расширенного воспроизводства описывается дифференциальным уравнением вида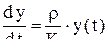 , (10.1)
, (10.1)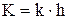 - капитальные затраты, необходимые для прироста на единицу интенсивности выпуска конечного продукта;
- капитальные затраты, необходимые для прироста на единицу интенсивности выпуска конечного продукта;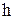 - усредненный коэффициент приростной фондоемкости по конечному продукту, численно равный приращению объема конечного проекта на 1 руб. капиталовложений;
- усредненный коэффициент приростной фондоемкости по конечному продукту, численно равный приращению объема конечного проекта на 1 руб. капиталовложений;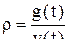 - доля конечного продукта; направляемая в фонд капитального строительства.
- доля конечного продукта; направляемая в фонд капитального строительства. , где
, где 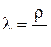 . (10.2)
. (10.2)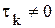 дифференциальное уравнение, описывающее процесс расширенного воспроизводства, примет вид
дифференциальное уравнение, описывающее процесс расширенного воспроизводства, примет вид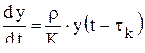 . (10.3)
. (10.3)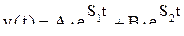 , (10.4)
, (10.4)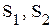 - корни характеристического уравнения
- корни характеристического уравнения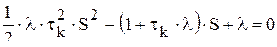 ; (10.5)
; (10.5) - коэффициенты, зависящие от параметров системы и начальных условий.
- коэффициенты, зависящие от параметров системы и начальных условий. , процесс воспроизводство носит колебательный характер и при
, процесс воспроизводство носит колебательный характер и при  решение дифференциального уравнения (10.3) имеет вид:
решение дифференциального уравнения (10.3) имеет вид: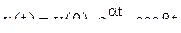 . (10.6)
. (10.6)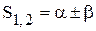 , интенсивность конечного выпуска изменяется по апериодическому закону и при
, интенсивность конечного выпуска изменяется по апериодическому закону и при 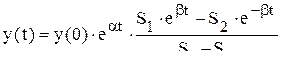 . (10.7)
. (10.7) − апериодический;
− апериодический;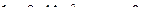 − колебательный.
− колебательный. расширенное воспроизводство обеспечивается при любом разделении конечного продукта на конечное потребление и инвестиции.
расширенное воспроизводство обеспечивается при любом разделении конечного продукта на конечное потребление и инвестиции.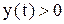 ,
, 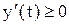 при
при  .
. ;
;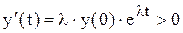 при любом
при любом 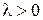 .
.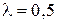 ;
; 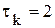 ;
; 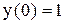 ;
; 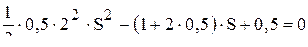 ,
, и
и 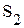
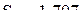 ;
; 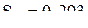 .
.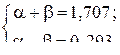
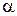 и
и 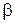 , которые составят
, которые составят  ,
, 
 .
.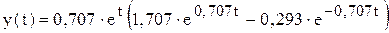 .
.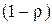 ?
?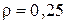 ,
,  . Определить, как следует изменить параметр
. Определить, как следует изменить параметр 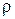 , чтобы через промежуток времени
, чтобы через промежуток времени 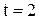 объем непроизводственного потребления удвоился.
объем непроизводственного потребления удвоился.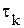 при
при 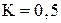 ; 1; 1,5, разделяющую области колебательного и апериодического процесса воспроизводства.
; 1; 1,5, разделяющую области колебательного и апериодического процесса воспроизводства.


