
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплопроводность при стационарном режимеСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
МЕТОДИЧЕСКОЕ ПОСОБИЕ для практических занятий раздела «Основы теории теплообмена» дисциплины ДН (М).Ф.4 Теплотехника
Направление 110300 Агроинженерия Бакалавриат
Уфа 2011
УДК 621.4 ББК 31.3
Методические указание разработаны доцентом Миграновым Д.Х. и переработаны доцентом Инсафуддиновым С.З.
Рекомендовано к печати кафедрой «Теплотехника и энергообеспечение предприятий» (протокол № от «» 20 г.) и методической комиссией энергетического факультета (протокол № от « » 20 г.).
Рецензент: доцент кафедры «Технология металлов и ремонт машин», к.т.н. Фаюршин А.Ф.
Ответственный за выпуск: зав. кафедрой «Теплотехника и энергообеспечение предприятий», к.т.н. Инсафуддинов С.З.
Оглавление
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
Примеры решения задач
Плоская стенка Пример 1.1 Стенка из красного кирпича длиной 15 м, высотой 3,5 м и толщиной 0,63 м имеет теплопроводность 0,81 Вт/(м·К). Температура на внутренней поверхности стенки 18°С, а на наружной - 30°С. Определить поверхностную плотность теплового потока, тепловой поток, а также потери теплоты через стенку в течение сутки.
Решение. Поверхностная плотность теплового потока
Тепловой поток
Потери теплоты через стенку в течении сутки. Q=Ф· t =3240·24·3600=279,936·106 Дж=279,936 МДж Пример 1.2 Плоская стенка топки выполнена из шамотного кирпича толщиной 250 мм. Температура внутренней поверхности стенки t1 =1350°C, наружной t2 =50°C. Теплопроводность шамотного кирпича зависит от температуры и определяется зависимостью l= lо(1+в t) =0,838(1+7·10-4 t). Построить график распределения температуры в стенке при х=0,50; 100; 150; 200 и 250 мм. Решение. В случае линейной зависимости теплопроводности от температуры поверхностная плотность теплового потока
где Тогда Температура на любом расстоянии х от поверхности стенки определяем по формуле
Решение. Эквивалентная теплопроводность многослойной стенки
q= A· q =12·60,4 =724,8 Вт. Определяем температуру наружной поверхности обшивки
Определяем температуру на поверхности краски
Определяем тепловой поток через эквивалентную теплопроводность lэкв .
ЗАДАЧИ 1.1 Определить теплопроводность материала стенки, если при толщине ее d =61 см и разности температур на поверхностях D t =50°C поверхностная плотность теплового потока q =67 Вт/м2. 1.2 В сушильную камеру со стенками толщиной 250 мм из строительного кирпича lс.к. =0,77 Вт/(м·К) с горячим воздухом подводится тепловой поток 650 кВт; 95% этого количества теплоты используется при сушке и затем отводится с рециркулирующим воздухом, а остальное теряется через стенки камеры поверхностью 210 м2. Температура наружной поверхности камеры 35°С. Определить температуру на внутренней поверхности сушильной камеры. 1.3 Холодильная камера отделена от цеха стенкой из строительного кирпича толщиной 50 см. lс.к. =0,81 Вт/(м·К), покрытой со стороны цеха штукатуркой lшт. =0,78 Вт/(м·К), а со стороны камеры – шлаковой ватой lш.в. =0,07 Вт/(м·К) и такой же штукатуркой. Толщина каждого слоя штукатурки dшт. =0,20 м. Температура воздуха в цехе 20°С при относительной влажности j =70%. Через стенку проникает тепловой поток 476,8 КДж на 1 м2 за 8 часов. Определить минимальную толщину слоя шлаковой ваты, при которой выпадение влаги на поверхность стенки со стороны цеха будет исключено. 1.4 Для уменьшения тепловых потерь стеной здания и повышения температуры внутренней поверхности кирпичной стены во избежание сырости в помещении применена изоляция слоем пенопласта толщиной 50 мм в вариантах.
Рисунок 1.7 Варианты применения изоляции стены здания слоем пенопласта. Определить процент сбереженной теплоты по сравнению с вариантом в; температуру кирпичной стены со стороны помещения в случае а, и кирпичной стены со стороны наружной поверхности в случае а и б. теплопроводность кирпичной кладки lкир =0,81 Вт/(м·К), пенопласта lпп =0,06 Вт/(м·К). Температура внутренней стенки 18,5°С, наружной стенки -7°С.
ЗАДАЧИ 1.7 Стальной паропровод диаметром 108/89 мм (l1 =50 Вт/(м·К)) имеет трех слойную изоляцию. Толщина первого слоя d2 =25 мм (l2 =0,06 Вт/(м·К)), второго - d3 =35 мм (l3 =0,07Вт/(м·К)) и третьего - d4 =4 мм (l4 =0,116Вт/(м·К)). Температура на внутренней поверхности трубы 180°С, на наружной поверхности третьего слоя t5 =50°С. Определить линейную плотность теплового потока и температуры на поверхностях стенки и слоя изоляции. 1.6 Змеевик испарителя холодильной машины изготовлен из труб нержавеющей стали диаметром 40/34 мм (lн.с. =20,9Вт/(м·К)). Змеевик погружен в раствор Na Cl концентрацией 18,8% по массе соли к массе раствора. Внутри змеевика испаряется холодильный агент, охлаждающий внутреннюю поверхность трубы до – 15,8°С. Линейная плотность теплового потока от раствора к холодильному агенту составляет 207 Вт/м. Будет ли испаритель при данном режиме охлаждения и концентрации раствора работать нормально или раствор будет намерзать на наружной поверхности труб. 1.7 Электронагреватель электрокотла для получения пара выполнен в виде нихромовой спирали на фарфоровом стержне, помещенный внутрь фарфоровой трубки диаметром 50/44 мм длиной 1 м (lф =1,04Вт/(м·К) имеет мощность 3,5 кВт. Разность между температурами наружной поверхности трубы и кипящей воды 7,6°С. Рассчитать температуру на внутренней поверхности трубы электронагревателя при давлении в котле 700 кПа. 1.8 Рассчитать плотность теплового потока на 1 м2 поверхности стальных труб (lст. =50Вт/(м·К) различных диаметров: 6/2; 10/6; 20/16; 30/26 мм, при условии, что температура поверхностей всех труб одинаковая и составляет 0,2°С. Расчет произвести по формуле для плоской стенки qпл и полученный результат сравнить с соответствующей величиной qср, полученный для цилиндрической стенки. 1.9 По плексигласовому трубопроводу диаметром 50/44 мм (lплекс. =0,184Вт/(м·К) течет пастеризованное молоко. Температура внутренней поверхности трубы t1 =80°C. Температура молока понижается в среднем на 1°С на каждые 10 м длины при скорости движения w =0,4 м/с. Удельная теплоемкость молока 3893 Дж/(кг×К), плотность rм =1030 кг/м3. Определить температуру наружной поверхности трубы. 1.10 Определить эквивалентную теплопроводность трехслойной цилиндрической стенки, который состоит из стальной трубы диаметром 50/40 (lст =45,3Вт/(м·К)), покрытой слоем изоляции толщиной 20 мм (lиз. =0,128Вт/(м·К), затем слоем минеральной ваты толщиной 50 мм (lмин.в. =0,07Вт/(м·К)). 1.11 Стальной трубопровод диаметром 60/50 мм (lст. =45,4Вт/(м·К)) холодильной установки имеет двухслойную изоляцию: слой мипоры толщиной 20мм (lмип. =0,041Вт/(м·К)) и слой минеральной ваты dм.в. =25 мм (lм.в. =0,07Вт/(м·К)). Определить относительное значение в процентах каждого из изоляционных слоев и стенки трубы в общем изолирующем эффекте конструкции.
1.12 Химический реактор, имеющий шаровую форму с наружным диаметром 950 мм имеет стенку толщиной 50 мм. Стена состоит из кварцевого стекла и нержавеющей стали с эквивалентной теплопроводностью l= 1,52 Вт/(м·К). Вследствие выделения теплоты при экзотермической реакции температура внутренней поверхности стенки стала 210°С, наружной - 80°С. Определить удельную тепловую нагрузку наружной и внутренней поверхности реактора. 1.13 Определить тепловые потери через стенку вращающегося шарообразного варочного котла, внутренний диаметр которого d1 =1,2 м, а общая толщина стенки котла и слоя изоляции d =80 мм. Температура внутренней поверхности 150°С, а внешней -40°С, эквивалентная теплопроводность lэкв. =0,1Вт/(м·К). 1.14 По нихромовому стержню диаметром 6 мм и длиной 500 мм проходит электрический ток. Разность потенциалов на кольцах стержня U =15 В. На поверхности стержня кипит вода под давлением р =0,5 МПа. Определить объемную производительность qv Вт/м3 внутренних источников теплоты, поверхностную плотность теплового потока q Вт/м2, линейную плотность теплового потока qe Вт/м и температуры на поверхности и оси стержня, если коэффициент теплообмена стержня и кипящей воды a =45000 Вт/(м2×К), удельное сопротивление стержня r =1,17 (Ом×мм2)/м. 1.15 Допустимая нагрузка для алюминиевых шин прямоугольного сечения 40х4 мм, установленных на ребро, не должна превышать 520 А. Максимальная температура шины при температуре окружающего воздуха tж =25°С должна быть не более to =70°C. Определить температуру поверхности шины и коэффициент теплообмена a с её поверхности, чтобы температура шины не превышала 70°С. Теплопроводность шины l =202 Вт/(м×К), удельное электрическое сопротивление алюминия r =0,295 (Ом×мм2)/м. Пример 1.8 Трубка из нержавеющей стали обогревается электрическим током путем непосредственного включения в электрическую цепь. Длина трубки l =450 мм, наружной диаметр 2,4 мм, внутренний 12 мм. Определить перепад температур в стенке трубки и силу тока J, пропускаемого по трубке, если отводимый тепловой поток от внешней поверхности трубки Ф =15 кВт. r =0,85 (Ом×мм2)/м; l =18,6 Вт/(м×К). Решение. Определяем электрическое сопротивление на единицу длины трубы
Тогда qe= J2 × Re отсюда Перепад температуры l стенки трубы
Пример 1.9 Трубка из нержавеющей стали с внутренним диаметром 10 мм и наружным диаметром 10,8 мм обогревается электрическим током путем непосредственного включения в цепь. Вся теплота отводится через внутреннюю поверхность трубки. Вычислить объемную производительность источников теплоты qv и перепад температур в стенке трубки, если по трубке течет ток силой 50 А r =0,65(Ом×мм2)/м; l =16,6Вт/(м×к). КОНВЕКТИВНЫЙ ТЕПЛООБМЕН Общие сведения Тепловой поток при конвективном теплообмене определяется по формуле:
Ф= aкА D t, (2.1) где aк – коэффициент теплообмена (теплоотдачи) конвекций, (Вт/(м2×К). Расчет коэффициента теплообмен выполняется в такой последовательности: - по условиям развития конвекции выбирается зависимость между числами подобия (эта зависимость обобщает эксперименты, выполненные на моделях); - рассчитываются числа подобия; - рассчитывается коэффициент теплообмена (теплоотдачи), исходя из значения числа Нуссельта. Числа подобия Число подобия естественного (свободного) движения жидкости – число Грасгофа, Gr= b g × D t × l3/ g2, определяет подъемную силу. Число подобия вынужденного движения жидкости – число Рейнольдса, Re= w × l/ g, определяет режим движения теплоносителя. Число Прандтля, Р r= n/ a, число подобия физических свойств теплоносителя. Число Нусельта, Nu= a × l/ l, определяет интенсивность теплоотдачи, где l – размер, определяющий характер развития конвекции, м. За этот размер принимают: - для труб – диаметр, d;
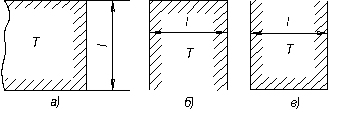
Рисунок 2.1 Схемы развития конвекции у поверхностей: а – вертикальный; б – верхний горизонтальный; в) нижний горизонтальный
- для замкнутых прослоек – зазор d; - для плоскостей (плит) – высота (рисунок 1а) или минимальный размер в плане (рисунок 1 б и в). - для каналов – эквивалентный диаметр, dэкв=4А/П, где А – площадь живого сечения потока, м2; П – полный (смоченный) периметр: независимо от того, какая часть этого периметра учитывается в теплообмене, м.
Примеры решения задач Пример 2.1 Температура поверхностей вертикальной стенки высотой 3 м равна 10°С. Температура воздуха в помещении 20°С. Определить коэффициент теплоотдачи от воздуха к стенке. Решение. Определяем значение критериев Gr и Pr Gr= b gl3 D t/ g2; Pr= g/ a. По таблице А1 приложения А по средней температуре tcp =0,5 (tc+ tв) =15°С определяем параметры воздуха g, l и Pr. gж =14,61×10-6 м2/с; Prж =0,705; lж =2,56×10-2 Вт/(м×К).
Gr × Pr =4,31×1010×0,705=3,03×1010 Режим движения воздуха турбулентный, так как Gr × Pr >109. По формуле (2.2) подставляя вместо С и т их значения при вертикальной поверхности находим число Нуссельта Nu =0,15 (Gr × Pr) 0,33 (Prж /Prc) 0,25=0,15(3,03×1010)0,33×1=431,48;
По приближенной формуле (2.3) для вертикальной поверхности aк Пример 2.2. Определить теплопотери через окно с двойным остеклением размерами 1,2х1,4 м2, если расстояние между стеклами 120 мм, температура поверхности стекол 18°С и -15°С.
Вычисляем произведение
Коэффициент конвекции eк =0,18(8,046×106)0,25=9,58 Тогда lэкв =9,58×24,6×10-3=2,36×10-1 Вт/(м×К). Теплопотери через окно с двойным остеклением будут равны
Пример 2.3 Определить силу тока для нихромовой проволоки диаметром 1,0 мм из условия, что ее температура не будет превышать 300°С. сопротивление 1 погонного метра проволки при температуре 300°С R=6,0 Ом, температура окружающей среды tm=20°C. Расчет произвести для двух случаев. - проволока находится в спокойном воздухе; - проволока находится в спокойной воде под давлением при температуре насыщения выше 300°С. Решение. По закону Ньютона-Рихмана определим мощность теплового потока от проволки к окружающей среде ql= p dн a(tc- tж). Для определения a находим число Грасгофа и число Нуссельта: а) окружающая среда воздух. По таблице А1 приложения А находим физические параметры воздуха при tопр =0,5(300+20)=160°С. lж =3,64×10-2 Вт/(м×К); gж =30,09×10-6 м2/с; Prж =0,682. Число Грасгофа
Gr × Pr =6,64×0,682=4,53. По таблице 2.1 при произведении Gr × Pr =4,778 C =7,18; т =0,125, тогда по формуле (2.2) Nu =1,18 (Gr × Pr) 0,125=1,18×4,530,125=1,435. ql= p dн × a(tc- tж) =3,14×0,001×52,2(300-20)=45,89 Вт/ч qe= J2 R Пример 2.4 В баке с раствором хлористого кальция размещен горизонтальный охлаждающий змеевик из труб, наружный диаметр которых 57 мм. Плотность раствора хлористого кальция при температуре 15°С rж =1220 кг/м3. Температура замерзания раствора t3 = -25,7°C, средняя температура наружной поверхности трубы tст =-20°С, температура раствора вдали от поверхности трубы tж =-10°С. Определить коэффициент теплообмена a от раствора к поверхности трубы при свободном движении жидкости. Решение. Теплоотдачу при свободном движении около горизонтальной трубы (змеевика) определяем по уравнению Nu =0,5 (Gr × Pr) 0,25. Определяющим размером является наружный диаметр трубы, в качестве определяющей температуры принимаем среднюю температуру
Данная формула справедлива 1×103 £(Gr × Pr) £103. Определяем теплофизические свойства хлористого кальция при r =1220 кг/м3 и t3 =-25,7°C l-20=0,523 Вт/(м×К) l-15=0,518 Вт/(м×К) l-20=0,511 Вт/(м×К) g -10=4,87×10 м2/с; g -15=6,20×10 м2/с; g =7,77×10 м2/с; Pr -10=33; Pr -15=42,5; Pr -20=53,80; b -10=3,5×10-4; b -20=3,3×10-4К1; b -15=3,4×10-4К1 Определяем критерии подобия, характеризующие процесс теплообмена:
Ra=(Grd × Prж)= (1,607×105×42,5)=6829750=6,83×106. Nuж. d =0,5(6,83×106)0,25=25,56 Коэффициент теплообмена Вынужденная конвекция При вынужденной конвекции между числами подобия существует зависимость Nu=cRen × Prm(Prm/Prc) 0,25 . (2.10) где коэффициенты с и п принимаем по таблице 2.2 в зависимости от вида движения теплоносителя. При ламинарном обтекании клинообразного тела Re <105 с углом раствора pв число Нуссельта определяется по формуле
При турбулентном обтекании - Re <105
Таблица 2.2 Значения коэффициентов с, п, и т в уравнении 2.10
При любых режимах движения теплоносителя число Нуссельта при обтекании шара определяется Nu =2+0,03 Pr 0,33× Re 0,54+0,35 Pr 0,35× Re 0,58 (2.13) В данном уравнении в качестве характерного размера принимается диаметр шара. Значение числа Нуссельта также можно определить по уравнению Кримера-Лооса: Nu =2+ Pr 0,33(0,4× Re 0,5+0,06 Re 0,67); (2.14) или по формуле Ранца-Маршалла: Nu =2+0,6 Pr 0,33 Re 0,5 (2.15) К рассчитанному по (2.10) числу Нуссельта необходимо ввести поправки на изменение среднего коэффициента теплообмена по длине трубы eе, на изгиб eизг, изменение теплоотдачи начальных рядов труб (цилиндра) при поперечном обтекании e i, поправочный коэффициент e y, учитывающий угол атаки (т.е. угол между осью цилиндра и вектором скорости среды), поправочный коэффициент e s, учитывающий влияние относительного шага es. Скорость потока, входящая в критерий Re определяется в самом узком сечении пучка как отношение объемного расхода жидкости V (м3/с) к площади S (м2) самого узкого сечения. a= aрас × eе × eизг × e i × eж × e s. (2.16) Поправка на изгиб труб (повороты, змеевики) рассчитывается по формуле eизг =1+1,77 d/R, (2.17) где d – диаметр трубы, м; R – радиус змеевика, м. Поправка на изменение среднего коэффициента теплоотдачи по длине трубы, канала при l/ d <50 в зависимости от режима движения принимается по таблице 2.3
Таблица 2.3 Поправочный коэффициент e l
Таблица 2.4 Поправочный коэффициент e y для пучков труб, расположенных под углом y к потоку жидкости
Поправка на изменение теплоотдачи в начальных рядах пучка труб принимается для: первого ряда e i =0,6; второго ряда коридорного пучка e i =0,9; второго ряда шахматного пучка e i =0,7; третьего и последующего рядов e i =1,0. Поправочный коэффициент e s, учитывающий влияние относительных шагов S1/ d и S1/ d
Рисунок 3 Рисунок 4 Схема коридорного расположения Схема шахматного расположения
Для коридорного пучка: e s=(S2/ d)- 0,15 Для шахматного пучка при S1/ S2 <2 e s=(S1/ S2) 1/6; при S1/ S2 ³2 e s =1,12. Среднее значение коэффициента теплоотдачи для всего пучка труб определяется по формуле
где a i - средний коэффициент теплоотдачи i -го ряда; Ai – суммарная поверхность теплообмена трубок i -го ряда; п – число рядов в пучке. Среднее значение коэффициента теплоотдачи в кольцевых каналах можно определить по уравнению Nu =0,017 Re 0,8× Pr 0,4(Pr ж /Prc)0,25(d2/d1)0,18, (2.19) где d1 – внутренний диаметр кольцевого канала; d2 – внешний диаметр. Формула (2.19) справедлива при d2/ d1 =1,2…14. l/ d =50…460 и Pr=0,7…100. Расчет теплоотдачи в пучках труб с круглыми и квадратными ребрами, обтекаемых поперечным потоком газа может быть произведен по следующим уравнениям в области значений 3×103< Re <25×103 и 3£ d/в £4,8, Nu= cRem(d/в) -0,54(h/в)-0,14, (2.20) где в – шаг ребр, h =0,5(D- d), где D – диаметр или сторона ребра, d – наружный диаметр трубы. с =0,104 для коридорных пучков труб с круглыми ребрами, для квадратных ребер с =0,096 и т =0,72 для обоих случаев. Для шахматных пучков с круглыми ребрами с=0,223; с квадратными ребрами с =0,205; в обоих случаях т =0,65. При продольном обтекании пластины воздухом расчетная формула (2.10) упрощается и принимает вид: - при ламинарном режиме Nu =0,57 Re 0,5; (2.21) - при турбулентном режиме Nu =0,32 Re 0,8; (2.22) aрас =5,9 w 0,8× l -0,2. (2.23) Для воздуха при вынужденном поперечном обтекании трубы можно применить формулу
Для поверхностей нагретой воды aрас =5,7+4,1 w, (2.25) где w - скорость движения теплоносителя, м/с; l – определяющий размер, м. Коэффициент теплоотдачи от горизонтальной трубы к воздуху при соответственной конвекции можно определить по формуле
Для условий вынужденной конвекции, обусловленной ветром aрас =4,65 w 0,7/ d 0,3. (2.27) где tн.п. – температура наружной поверхности, °С; to – температура окружающей среды, °С; d2 – наружный диаметр трубы, изоляции, м. Пример 2.5 Через трубу диаметром 50 мм длиной 3 м изогнутой в виде змеевика диаметром 600 мм протекает горячая вода с температурой 50°С со скоростью w =0,8 м/с. Определить коэффициент теплоотдачи a от стенки к воде, если температура стенки tc =70°С. Решение. Определяем параметры воды при tж =50°С и tc =70°C по таблице А5 приложения А. при tж =50°С lж =0,648 Вт/(м×К); gж =5,56×10-7 м2/с; Prж =3,54. при tс =70°С lж =0,668 Вт/(м×К); gж =4,15×10-7 м2/с; Prс =2,55. Рассчитываем число Рейнольдса и число Нуссельта: Re = w d/ gж =0,8×0,05/5,56×10-7=7,2×104; Nu =0,021 Re 0,8 Pr ж 0,43(Pr ж /Prc)0,25=0,021(7,2×104)0,8×3,540,43×(3,54/2,55)0,25=303. Вводим поправки eе и eизг l/d =3/0,05=60>50 e e =1; eизг =1+1,77 d/R =1+1,77×50/300=1,295. Тогда
Пример 2.6 Определить средний коэффициент теплоотдачи в воздухоподогревателе с поперечным восьмирядным коридорным расположением труб к потоку воздуха. Диаметр труб d =16 мм; S1 =1,5 d; S2 =2,0 d. Средняя скорость воздуха в узком сечении 10 м/с, температура на входе 20°С, на выходе 60°С. Решение. По средней температуре воздуха tср =0,5 Рассчитываем число Рейнольдса Пользуясь формулой (2.10) из таблицы 2.2 для поперечного пучка труб при Re=103…105 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 579; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.149.186 (0.012 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

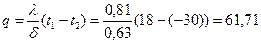 Вт/м2.
Вт/м2.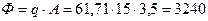 Вт
Вт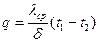 ,
,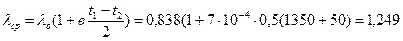 Вт/(м·К).
Вт/(м·К).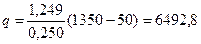 Вт/м2.
Вт/м2.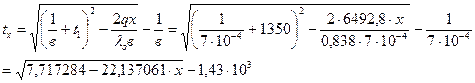
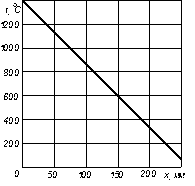 Рисунок 1.6
Рисунок 1.6
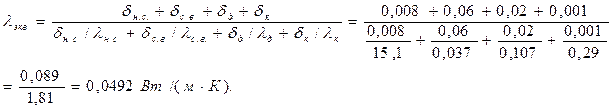
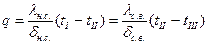 из данного уравнения находим
из данного уравнения находим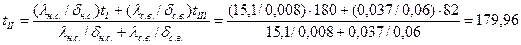 °С.
°С.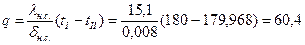 Вт/м2.
Вт/м2.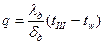
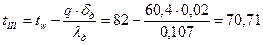 °С
°С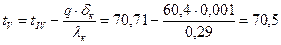 °С.
°С.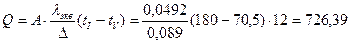 Вт
Вт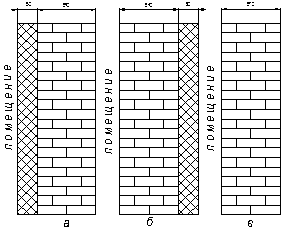
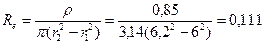 Ом/м
Ом/м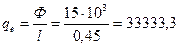 Вт/м
Вт/м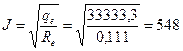 А
А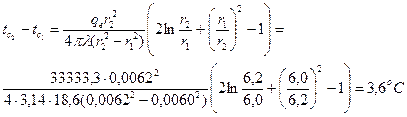
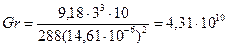 ;
;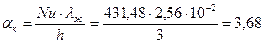 Вт/(м2×К).
Вт/(м2×К).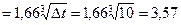 Вт/(м2×К).
Вт/(м2×К).
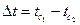 , за определяющую температуру
, за определяющую температуру 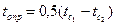 ; tопр =0,5(18-15)=1,5°С. По таблице А1 приложения А определяем параметры воздуха
gж =13,41×10-6 м2/с; lж =24,6×10-3 Вт/(м×К);
Pr =0,71;
; tопр =0,5(18-15)=1,5°С. По таблице А1 приложения А определяем параметры воздуха
gж =13,41×10-6 м2/с; lж =24,6×10-3 Вт/(м×К);
Pr =0,71;
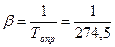 К-1.
К-1.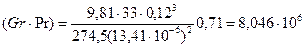 .
.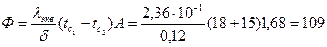 Вт
Вт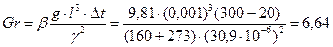
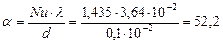 Вт/(м2×К).
Вт/(м2×К).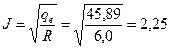 А
А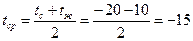 °С.
°С.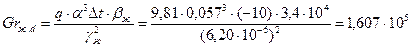
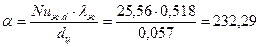 Вт/(м2×К).
Вт/(м2×К).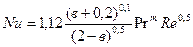 т =1/3+0,067в-0,026в2 . (2.11)
т =1/3+0,067в-0,026в2 . (2.11)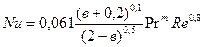 т =1/3+0,067в-0,026в2 . (2.12)
т =1/3+0,067в-0,026в2 . (2.12)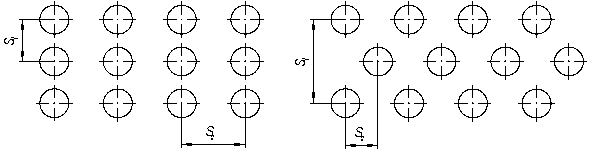
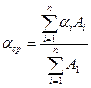 , (2.18)
, (2.18)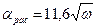 . (2.24)
. (2.24)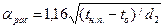 . (2.26)
. (2.26)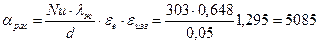 Вт/(м2×К).
Вт/(м2×К).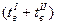 =0,5(20+60)=40°С из таблицы А1 приложения А находим физические параметры воздуха: l =27,6×10-3 Вт/(м×К); n =16,96×10-6 м2/с и число Прандтля Pr =0,70.
=0,5(20+60)=40°С из таблицы А1 приложения А находим физические параметры воздуха: l =27,6×10-3 Вт/(м×К); n =16,96×10-6 м2/с и число Прандтля Pr =0,70.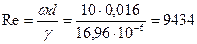 .
.


