
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конвективный теплообмен через зернистый слойСодержание книги Поиск на нашем сайте
При расчете коэффициента теплообмена через зернистый слой применяется уравнение В.Н. Тимофеева при 20< Reж <200 Nuж =0,124 Reж × Pr 0,43 (2.28) при Reж >200 Nuж =0,711 Reж 0,67× Pr 0,43 (2.29) Или же уравнения при 20< Reж <200 Nuж =0,106 Reж (2.30) при Reж >200 Nuж =0,61 Reж (2.31) Пример 2.10 Слой яблок охлаждается потоком воздуха. Средний размер яблок d=45 мм. Температура воздуха, входящего в слой Определить коэффициент теплообмена a от поверхности яблок к воздуху. Решение. По приложению А таблица А1 определяем теплофизические параметры воздуха при средней температуре lж =2,51×10-2 Вт/(м×К); gж =14,16×10-6 м2/с, Prж =0,705. Критерий Рейнольдса по (2.31) Nuж =0,61 Re 0,67=0,61×(1779)0,67=91,82
Пример 2.11 Слой гравия охлаждается водой. Средний размер частиц d =27 мм. Температура воды входящей в слой гравия 5°С, а выходящий из него Решение. По средней температуре воды q= a(tc- tж); Число Нуссельта Предполагая, что Reж >200 по (2.29) находим число Нуссельта Nuж =0,711 Reж 0,67× Pr 0,43. Число Рейнольдса
Re=40,661/0,67=252,19; Задача. Слой зерна после сушилки охлаждается воздухом, средней размер зерна d =8 мм. Температура воздуха входящего в слой зерна 5°С, выходящего из него 20°С. Скорость фильтрации 0,5 м/с. Определить коэффициент теплоотдачи от зерна к воздуху. Теплоотдача суспензий Во многих отраслях промышленности и сельского хозяйства приходится нагревать или охлаждать жидкостные суспензии мелкодисперсного порошка твердого тела в жидкости. Согласно экспериментам проводимым в МВТУ им. Н.Э. Баумана Кафановым В.И. критериальное уравнение теплообмена при течении жидкостных суспензий в трубах имеет вид
где Nuс – критерий Нуссельта суспензии; Rec – критерий Рейнольдса суспензии; Prc – критерий Прандтля суспензии; r – объемная доля порошка твердого тела в суспензии rж – плотность жидкости, кг/м3; rт - плотность твердого тела, кг/м3;
dтр и dr – диаметр трубы и средней диаметр частиц порошка твердого тела. В качестве определяющей температуры принимают среднюю температуру среды tср=(t1+ t2)/2, где t1 – температура среды на входе в теплообменник, а t2 – на выходе из него, °С. Коэффициент гидравлического сопротивления x определяют по формуле:
Теплопроводность суспензии lс определяют по формуле Максвелла
где lж – теплопроводность жидкости, Вт/(м×К); lт – теплопроводность твердого тела, Вт/(м×К). Динамическая вязкость суспензии mс определяют по формуле Вэнда mс= mж (1+2,5 r +7,17 r 2+16,2 r 3), (2.35) где mж – динамическая вязкость жидкости, Па×с. Выше перечисленными зависимостями можно пользоваться до 25% концентрации по объему. Пример 2.12 По трубопроводу диаметром 50 мм и длиной 4 м протекает суспензия порошка меди в воде со скоростью w =1 м/с. Объемная концентрация меди 10%, средний диаметр частиц порошка 100×10-6 м. Определить количество теплоты передаваемой суспензии за 1 час, если температура жидкости 50°С, а температура стенки 70°С, а также коэффициент теплообмена a. Решение. Подсчитываем отдельные множители, входящие в управление (2.32). Теплофизические параметры берем из приложения А таблица А5 и таблица Б1 приложения Б. rс= rт r+ rж(i+r) =8930×0,1+988,1(1+0,1)=1769,29 кг/м3 По формуле (2.35) определяем динамическую вязкость суспензии mс= mж (1+2,5 r +7,17 r 2+16,2 r 3)=543,4×10-6(1+2,5×0,1+7,17×(0,1)2+16,2(0,1)3=735×10-6 Н×с/м2=735×10-6 Па×с. По формуле (2.34) находим lс суспензии
По формуле вычисляем теплоемкость суспензии. Находим число Рейнольдса Число Прандтля Число Нуссельта
Находим коэффициент теплообмена aс
По закону Ньютона-Рихмана Ф= aс ×А(tс- tж) =5824×3,14×0,05×4×20=73149 Вт
|
|||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 196; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.188.195 (0.007 с.) |

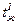 =0°С, выходящего из него -
=0°С, выходящего из него - 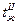 =20°С. Скорость фильтрации w=0,6 м/с.
=20°С. Скорость фильтрации w=0,6 м/с.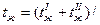 2=(0+20)/2=10°С.
2=(0+20)/2=10°С.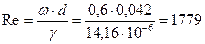 .
.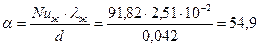 Вт/(м2×К).
Вт/(м2×К).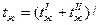 2=(5+20)/2=12,5°С по приложению А таблица А5 определяем теплофизические свойства воды lж =57,95×10-2 Вт/(м×К); gж =1,246×10-6 м2/с, Prж =9,05 при tст=25°С Prc=6,22.
2=(5+20)/2=12,5°С по приложению А таблица А5 определяем теплофизические свойства воды lж =57,95×10-2 Вт/(м×К); gж =1,246×10-6 м2/с, Prж =9,05 при tст=25°С Prc=6,22.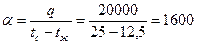 Вт/(м2×К).
Вт/(м2×К).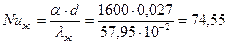 .
.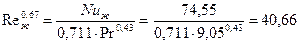 .
.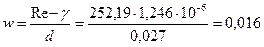 м/с.
м/с.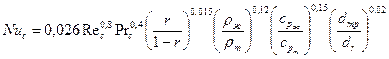 , (2,32)
, (2,32)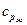 и
и 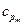 - теплоемкости жидкости и твердого тела, кДж/(кг×К);
- теплоемкости жидкости и твердого тела, кДж/(кг×К);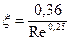 . (2.33)
. (2.33)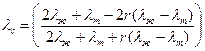 , (2.34)
, (2.34)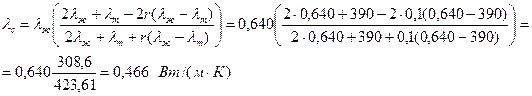
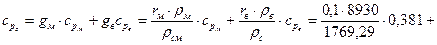
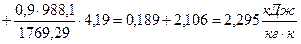
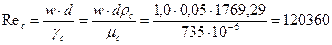 .
.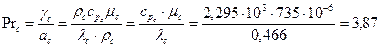
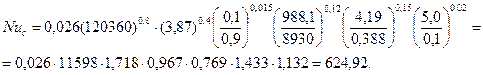
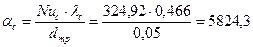 Вт/(м2×К)
Вт/(м2×К)


