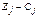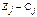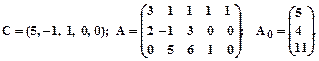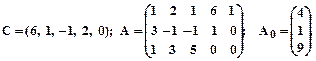Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В. Ф. Казак, Е. В. Морозова, И. Э. СимоноваСодержание книги
Поиск на нашем сайте
В. Ф. Казак, Е. В. Морозова, И. Э. Симонова
Методы Оптимальных решений МИНОБРНАУКИ РОССИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» КАМЫШИНСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (ФИЛИАЛ) ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ОБРАЗОВАНИЯ «ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
В. Ф. Казак, Е. В. Морозова, И. Э. Симонова Методы оптимальных решений
Учебно-методическое пособие
Волгоград 2016
УДК
Рецензенты:
Печатается по решению редакционно-издательского совета Волгоградского государственного технического университета
Казак, В. Ф. Методы оптимальных решений: учебно-методическое пособие / В. Ф. Казак, Е. В. Морозова, И.Э. Симонова; ВолгГТУ. – Волгоград, 2016. – 110 с.
ISBN
Излагается теоретическое обоснование методов математического моделирования (основные понятия, теоремы, алгоритмы) и приводятся примеры их применения. Предназначено в помощь студентам, изучающим дисциплины «Методы оптимальных решений», «Теория принятия решений» и др..
Ил.: 28. Табл.: 42. Библиогр.: 7 назв.
ISBN Ó Волгоградский государственный
университет, 2016 ОГЛАВЛЕНИЕ
ПРЕДМЕТ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ.
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ Построение математических моделей простейших Экономических задач 1. Задача использования сырья Пусть некоторая производственная единица (цех, завод и т. д.), исходя из конъюнктуры рынка, технических возможностей может выпускать п различных видов продукции. Предприятие при их производстве должно ограничиться каким-то количеством различных видов ресурсов (сырье, полуфабрикаты, рабочая сила, оборудование, электроэнергия и т. д.). Пусть их число равно т. Рассмотрим задачу на конкретном примере. Для изготовления двух видов продукции Р1, Р2 используют три вида сырья S1, S2, S3. Запасы сырья, количество единиц продукции, а также величина прибыли, получаемая oт реализации единицы продукции, приведены в табл. 1. Таблица 1
Необходимо составить такой план выпуска продукции, чтобы при ее реализации получить максимальную прибыль. Обозначим через х1 – количество изготовленных единиц продукции Р1, х2 – количество изготовленных единиц продукции Р2. Тогда, учитывая количество единиц сырья, идущих на изготовление единицы продукции, а также запасы сырья, получим систему ограничений: Также на х1 и х2 должно быть наложено ограничение неотрицательности х1 ³ 0, х2 ³ 0. Конечную цель решаемой задачи – получение максимальной прибыли при реализации продукции, выразим как функцию цели Z = 50х1 + 40х2 (руб.). Числа х1, х2 могут быть и дробными, так как в задаче не оговорены условия целочисленности. Итак, мы построили математическую модель задачи использования сырья (ресурсов): найти max значение целевой функции Z = 50 х1 + 40 х2 при ограничениях
Обобщим эту задачу (табл. 2). Таблица 2
Математическая модель задачи Пусть дан план
2. Задача о смесях. В различных отраслях народного хозяйства возникает проблема составления таких рабочих смесей на основе исходных (имеющихся) материалов, которые обеспечивали бы получение конечного продукта. К этой группе задач относятся задачи о выборе диеты, составления рациона в животноводстве, шихты в металлургии, смесей для получения бетона и т. д. Мы остановимся на примере задачи составления рациона. При откорме каждое животное ежедневно должно получить не менее 9 единиц питательного вещества S1, не менее 8 единиц вещества S2 и не менее 12 единиц вещества S3. Для составления рациона используют два вида корма. Содержание количества единиц питательных веществ в 1 кг каждого вида корма и стоимость 1 кг корма приведены в табл. 3. Таблица 3
Необходимо составить дневной рацион нужной питательности, причем затраты на него должны быть min. Для составления математической модели обозначим через x1, x2 – количество килограммов корма соответственно 1 и 2 в дневном рационе:
Цель данной задачи – добиться min затрат на дневной рацион, поэтому общую стоимость рациона можно выразить целевой функцией Z = 4x1 + 6x2. Задачу составления рациона можно обобщить, если предусмотреть в рационе т видов питательных веществ в количестве не менее В i (i =
Помимо этих задач, можно привести примеры задач о раскрое материалов, о размещении заказа, транспортной задачи и т. д. Симплексные таблицы. Признак оптимальности опорного плана Итак, любую задачу линейного программирования можно представить в предпочтительном виде: max(min) Z =
хj ³ 0, (j = Рассмотрим эту задачу для n = 4, m = 2 (и распространим ее для общего случая): Z = c1x1 + c2x2 + c3x3 + c4x4.
Выразим базисные переменные (БП) х1, х2 через свободные х3 и х4
x2 =
Введем обозначения в общем виде:
где С учетом этих равенств целевая функция примет вид: max(min)Z= В общем случае задачу записывают в таблицу, которая называется симплексной (табл. 17). Таблица 17
Последнюю строку называют индексной строкой, число Теорема. Пусть исходная задача решается на max. Если для некоторого опорного плана все оценки Δj (j = Доказательство: Так как Z = ΔO Теорема. Если исходная задача решается на min и для некоторого опорного плана все оценки Δj (j = Пример 9. Решить задачу линейного программирования.
Система ограничений задачи имеет предпочтительный вид: базисом являются переменные х2,х4,х1. Заносим условие задачи в симплексную таблицу (табл. 18): Таблица 18
Заполним индексную строку (Z j – с j): ΔO = – 1 × 1,5 – 2 × 2 + 2 × 0,5 = – 4,5, Δ1 = – 1× 0 – 2 × 0 + 2 × 1 – 2 = 0, Δ2 = – 1× 1 – 2×0 + 2×0 – (–1) = 0, Δ3 = – 1× 0,5 – 2 + 2 × (– 0,5) – 3= – 6,5, Δ4 = – 1× 0 – 2×1 + 2×0 – (– 2) = 0, Δ5 = – 1× 0,5 – 2 × 0 + 2 × 0,5 – 1 = – 0,5. Начальный опорный план
3.3. Переход к нехудшему опорному плану Пусть решается задача линейного программирования с системой ограничений в предпочтительном виде
ее начальный опорный план Рассмотрим задачу на mах: если все Δ j ³ 0, то опорный план оптимален. Пусть существует jO, для которого ΔjO < 0. Вектор столбец x i = B I –
При значительном увеличении Итак, xjo можно увеличивать до тех пор, пока B i – xjo = min (если это условие выполняется при нескольких i, то в качестве i O можно выбрать любое) Cтроку xm+1 = 0, …,
xm = Новый базис будет состоять из переменных х1, В результате преобразований получен новый опорный план Практика показывает, что в случае решения задачи на max число шагов уменьшается, если разрешающий столбец выбрать по правилу max В случае задачи на min разрешающий столбец нужно выбирать по правилу mах Δj (Δj > 0). Далее процесс повторяется. Проверяем, является ли план Шаг симплексного метода, позволяющий перейти от одного опорного плана к другому нехудшему, называется итерацией. Симплексные преобразования нового базиса выполняются по правилу: 1. Элементы строки i O новой таблицы равны соответствующим элементам разрешающей строки старой таблицы, деленным на разрешающий элемент: 2. Элементы разрешающего столбца j0 новой таблицы равны 0, за исключением 3. Чтобы найти любой другой элемент новой симплексной таблицы, нужно воспользоваться правилом прямоугольника и полученное число разделить на разрешающий элемент. 4. По 3 пункту вычисляются и элементы индексной строки. Для контроля вычислений они могут быть рассчитаны по формулам Пример 10. Найти max Z = 14х1 – 5х2 + 2х3 – х4 + 8х5, если
Решение. Так как задача имеет предпочтительный вид, то занесем ее условия в симплексную табл. 19 (итерация 0). Таблица 19
0 итерация: исходная задача на max, поэтому начальный опорный план
1 итерация: 1) выбираем разрешающий элемент из условия: max {|Δ1|, |Δ5|} = m a x (4; 1) = 4 – это соответствует 1 столбцу, поэтому его выбираем за разрешающий то есть X1 будем вводить в базис. Для определения разрешающей строки находим минимальное симплексное отношение:
итак, 1 – строка разрешающая =>элемент а11 = 1 – разрешающий; 2) переменную х2 выведем из базиса, а х1 введем в базис; 3) разрешающую строку делим на разрешающий элемент; 4) элементы разрешающего столбца заполняем нулями; 5) остальные элементы пересчитываем по правилу прямоугольника и делим на разрешающий элемент. Делаем контрольные проверки:
Так как существует отрицательная оценка ∆5 = – 5, план 2 итерация: 1) разрешающий столбец 5, переменную. х5,будем вводить в базис. 2) определяем разрешающую строку: min симплексное отношение 3) разрешающую строку делим на 8; 4) в разрешающем столбце проставляем нули; 5) остальные элементы пересчитываем; 6) делаем контрольные проверки, так же как и в итерации 1, так как все Dj ³ 0, опорный план Ответ: Пример 11. Решить М-задачу линейного программирования: Найти: min Z = 3x1 + 2х2 + 3х3, если Решение: Сведем задачу к каноническому виду и введем искусственные переменные
Занесем условие М-задачи в симплексную таблицу (индексную строку записываем в две строки: в первой – слагаемые без М, во второй – слагаемые с М) (табл. 20). Таблица 20
Окончание табл. 20
Примечание: по мере вывода из базиса искусственных переменных соответствующие им столбцы можно опускать.
Так как все Dj ≤ 0, то план оптимален, Ответ: Замечания: 1. Если в индексной строке последней симплексной таблицы, содержащей оптимальный план, имеется хотя бы одна нулевая оценка, соответствующая свободной переменной, то задача линейного программирования имеет бесконечное множество оптимальных планов. 2. Если в индексной строке симплексной таблицы задачи линейного программирования на max содержится отрицательная оценка Dj < 0, а в соответствующем столбце переменной хj. нет ни одного положительного элемента, то целевая функция на множестве допустимых планов задачи не ограничена сверху. Если же задача линейного программирования на min и в индексной строке содержится положительная оценка Dj > 0, а в столбце переменной хj нет ни одного положительного элемента, то на множестве допустимых планов целевая функция не ограничена снизу. С экономической точки зрения неограниченность целевой функции задачи линейного программирования говорит только об одном; разработанная модель недостаточно точна (бессмысленно говорить о бесконечной прибыли). Типичными ошибками, приводящими к построению моделей такого рода, являются: а) неполный учет ограничений, которые являются существенными в данной задаче; б) небрежные оценки параметров, которые участвуют в ограничениях.
Задания для самостоятельной работы Задание 1. Для изготовления двух видов продукции P1 и P2 используют три вида сырья (S1, S2, S3). На изготовление единицы продукции P1 используют сырье S1 – a1 (ед.), S2 – a2 (ед.), S3 - a3 (ед.). На изготовление единицы продукции P2 используют сырье S1 – b1 (ед.), S2 – b2 (ед.), S3 – b3 (ед.). Запасы сырья S1 составляют не более чем k1, сырья S2 – не более чем k2, сырья S3 – не более чем k3. Прибыль от единицы продукции P1 составляет a руб., от P2 составляет b руб. Необходимо составить такой план выпуска продукции, чтобы при ее реализации получить максимальную прибыль. Данные для выполнения задания соответствующего варианта представлены в табл. 21. Таблица 21
Окончание табл. 21
Заданеи 2. Задана каноническая модель задачи линейного программирования. Z = CX, AX = A0, X ³ 0, A = (aij)3 х 5. Требуется найти max Z М- методом. 1.
2.
3.
4.
5. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



 технический
технический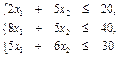 (количество сырья, идущего на изготовление продукции, не должно превышать запасы сырья).
(количество сырья, идущего на изготовление продукции, не должно превышать запасы сырья).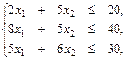
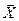 = {x1, x2, … xn} где xj – количество изготовленной единиц j продукции. Тогда требуется найти целевую функцию Z = c1x1 + c2x2 + … + cnxn при ограничениях (условиях):
= {x1, x2, … xn} где xj – количество изготовленной единиц j продукции. Тогда требуется найти целевую функцию Z = c1x1 + c2x2 + … + cnxn при ограничениях (условиях):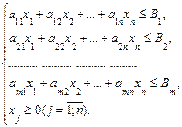
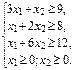
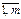 ) и использовать n видов кормов. Обозначим через а ij − количество единиц i-го питательного вещества, содержащего-ся в единице j-го корма, c j − стоимость единицы j корма, x j – количество единиц j-го корма в дневном рационе. Тогда, требуется найти min Z = с1х1 + с2х2 + … + сn хn, при ограничениях:
) и использовать n видов кормов. Обозначим через а ij − количество единиц i-го питательного вещества, содержащего-ся в единице j-го корма, c j − стоимость единицы j корма, x j – количество единиц j-го корма в дневном рационе. Тогда, требуется найти min Z = с1х1 + с2х2 + … + сn хn, при ограничениях: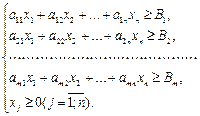
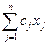 ,
,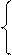 xi +
xi + 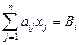 , Bi ³ 0, (i =
, Bi ³ 0, (i = 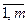 ),
),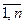 ).
).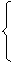
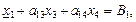
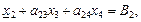
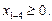
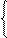 x1 =
x1 = 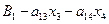 ,
,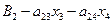 и подставим их в целевую функцию
и подставим их в целевую функцию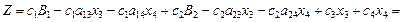
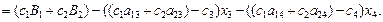
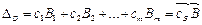 ,
,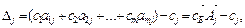
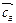 = (с1; с2; …; сm) – вектор коэффициентов целевой функции при базисных переменных,
= (с1; с2; …; сm) – вектор коэффициентов целевой функции при базисных переменных, 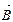 = (B1; B2;..; Bm) – вектор свободных членов;
= (B1; B2;..; Bm) – вектор свободных членов; 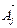 =
= 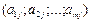 – вектор коэффициентов при переменных х j.
– вектор коэффициентов при переменных х j.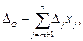 где
где 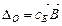 ;
; 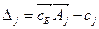
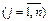 .
.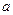 1, m+1 …
1, m+1 … 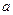 1n
0 1 … 0 … 0
1n
0 1 … 0 … 0 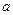 2, j …
2, j … 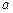 m, m+1 …
m, m+1 … 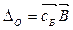 – значение целевой функции для начального опорного плана
– значение целевой функции для начального опорного плана 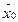 , т. е. ΔO = Z(
, т. е. ΔO = Z(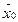 ) =
) = 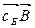 , числа
, числа 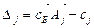 – называются оценками свободных переменных.
– называются оценками свободных переменных.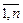 ) не отрицательны (больше или равны 0), то такой план оптимален.
) не отрицательны (больше или равны 0), то такой план оптимален.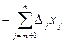 и Δj ³ 0, то Z достигает max, когда
и Δj ³ 0, то Z достигает max, когда 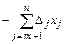 = 0, а это возможно, если хm+1 = 0, хm+2 = 0,..., хn = 0, т. е. опорный план (В1, В2, …, Вm, 0, …, 0) – оптимален.
= 0, а это возможно, если хm+1 = 0, хm+2 = 0,..., хn = 0, т. е. опорный план (В1, В2, …, Вm, 0, …, 0) – оптимален. ) не положительны (меньше или равны 0), то такой план оптимален.
) не положительны (меньше или равны 0), то такой план оптимален.
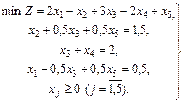 =>
=>
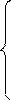
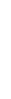
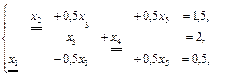
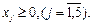
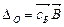 ,
, 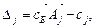
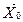 = (0,5; 1,5; 0;2; 0), Z (
= (0,5; 1,5; 0;2; 0), Z (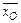 ) = – 4,5. Так как все оценки индексной строки Δ j не положительны, а задача на min, то план
) = – 4,5. Так как все оценки индексной строки Δ j не положительны, а задача на min, то план 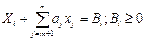 (i =
(i = 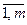 ), (5)
), (5)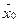 = (В1, В2, …, Вm, 0, …, 0). Значение целевой функции Z(
= (В1, В2, …, Вm, 0, …, 0). Значение целевой функции Z(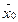 ) =
) = 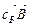 = ΔO.
= ΔO.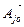 , для которого ΔjO < 0, называется разрешающим, а соответствующая переменная xjo – перспективной. Попытаемся, не изменяя нулевых значений свободных переменных хm+1, хm+2, …, хn, кроме xjo увеличить значение целевой функции Z за счет увеличения переменной xjo > 0. Однако увеличивать xjo надо осторожно, так как выбор
, для которого ΔjO < 0, называется разрешающим, а соответствующая переменная xjo – перспективной. Попытаемся, не изменяя нулевых значений свободных переменных хm+1, хm+2, …, хn, кроме xjo увеличить значение целевой функции Z за счет увеличения переменной xjo > 0. Однако увеличивать xjo надо осторожно, так как выбор 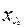 влияет на значения х1,..., хm, которые должны быть ³ 0. Имеем: х1 ³ 0, х2 ³ 0,..., хm ³ 0, хm+1 = 0,..., xjo-1 = 0, xjo > 0, xjo+1 = 0,..., xn = 0 и из (5) имеем
влияет на значения х1,..., хm, которые должны быть ³ 0. Имеем: х1 ³ 0, х2 ³ 0,..., хm ³ 0, хm+1 = 0,..., xjo-1 = 0, xjo > 0, xjo+1 = 0,..., xn = 0 и из (5) имеем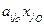 – (i =
– (i = 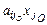 , значит получим хi < 0, что недопустимо. В случае, если
, значит получим хi < 0, что недопустимо. В случае, если 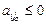 (i =
(i = 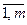 ), такого нарушения не произойдет.
), такого нарушения не произойдет.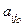 xjo ³ 0, не нарушая общности, можно считать
xjo ³ 0, не нарушая общности, можно считать 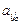 > 0, тогда
> 0, тогда 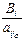 . Найдем среди отношений
. Найдем среди отношений 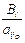 наименьшее. Пусть оно называется наименьшим симплексным отношением и обозначается Q.
наименьшее. Пусть оно называется наименьшим симплексным отношением и обозначается Q.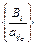 =
= 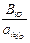 = Q,
= Q,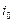 называют разрешающей, элемент
называют разрешающей, элемент 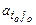 – разрешающим. Переменная
– разрешающим. Переменная 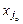 , присутствующая в базисе, является неперспективной и ее выводят из базиса:
, присутствующая в базисе, является неперспективной и ее выводят из базиса: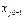 = 0,
= 0, 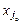 = Q,
= Q,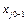 = 0, …, xn = 0, а из равенства (6) находим: x1 = B1 –
= 0, …, xn = 0, а из равенства (6) находим: x1 = B1 – 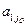 Q, …,
Q, …,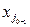 =
= 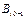 –
– 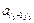 Q,
Q, 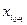 =
= 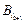 –
– 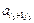 Q, …,
Q, …,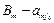 Q.
Q.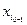 ,..., xm, а соответствующий ему опорный план примет вид, X1 = (B1 –
,..., xm, а соответствующий ему опорный план примет вид, X1 = (B1 – 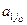 Q; B2 –
Q; B2 – 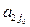 Q; …;
Q; …; 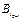 –
– 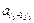 Q; 0;
Q; 0; 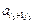 Q; …;
Q; …; 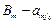 Q; 0; …; Q; 0; …; 0).
Q; 0; …; Q; 0; …; 0).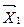 , в котором переменная
, в котором переменная 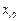 заменена на
заменена на 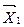 не хуже начального
не хуже начального 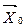 .
.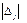 (Δj £ 0), т. е. в базис вводить переменную, которой соответствует max по абсолютной величине оценки.
(Δj £ 0), т. е. в базис вводить переменную, которой соответствует max по абсолютной величине оценки.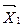 оптимальным, если да, то задача решена. Если нет, то переходим к нехудшему опорному плану
оптимальным, если да, то задача решена. Если нет, то переходим к нехудшему опорному плану 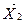 и т. д.
и т. д.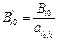 ,
, 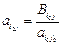 , (j =
, (j = 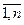 ).
).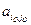 = 1.
= 1.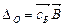 ,
, 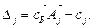
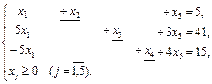
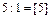
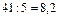
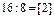
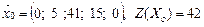 . Он неоптимальный, так как Δ1 < 0, Δ5 < 0.
. Он неоптимальный, так как Δ1 < 0, Δ5 < 0.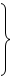
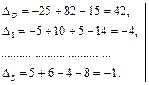
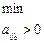
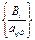 =
= 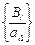 =
= 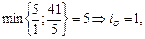
 14 – 5 + 2×16 – 1× 40 = 62;
14 – 5 + 2×16 – 1× 40 = 62; 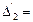 14 – 10 – 5 + 5 = 4;
14 – 10 – 5 + 5 = 4;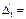 14 + 0 + 0 – 14 = 0;
14 + 0 + 0 – 14 = 0; 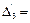 0 + 2 + 0 – 2 = 0;
0 + 2 + 0 – 2 = 0;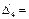 0 + 0 – 1 + 1 = 0;
0 + 0 – 1 + 1 = 0; 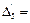 – 14 + 16 + 1 – 8 = – 5 < 0.
– 14 + 16 + 1 – 8 = – 5 < 0. = (5; 0; 16; 40; 0) не оптимальный, Z(x1) = 62 > Z (
= (5; 0; 16; 40; 0) не оптимальный, Z(x1) = 62 > Z (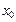 ) = 42.
) = 42.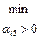
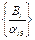 =
= 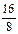 = 2 соответствует 2-ой строке, значит переменную х3 выводим из базиса. Разрешающий элемент а25 = 8;
= 2 соответствует 2-ой строке, значит переменную х3 выводим из базиса. Разрешающий элемент а25 = 8;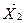 – оптимален
– оптимален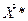 = (7; 0; 0; 42; 2), Z(
= (7; 0; 0; 42; 2), Z(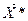 ) = 72.
) = 72.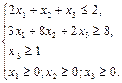
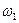 и
и 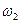 :
:
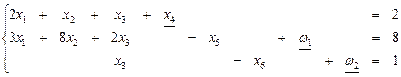
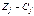
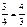 1/
1/ 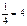 1/1=[1]
1/1=[1]