
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Введение. Предмет математического программированияСодержание книги
Поиск на нашем сайте
Многие задачи, с которыми приходится иметь дело в повседневной практике, являются многовариантными. Среди множества возможных вариантов в условиях рыночных отношений приходится находить наилучшие в некотором смысле при ограничениях, налагаемых на природные, экономические и технологические возможности. До недавнего времени большинство таких задач решалось, исходя из здравого смысла и опыта лиц, принимающих решения или просто «на глаз». При таком подходе не было и не могло быть никакой уверенности, что найденный вариант наилучший, а при современных масштабах производства даже незначительные ошибки оборачиваются громадными потерями. В связи с этим возникла необходимость применять для анализа экономической ситуации математические методы и вычислительную технику. Такие методы объединяются под общим названием математическое программирование или математическое моделирование. Математическое программирование − область математики, разрабатывающая теорию и численные методы решения многомерных экстремальных задач с ограничениями, т. е. задач на экстремум функции многих переменных с ограничениями на область определения этих переменных. Функция, экстремальное значение которой нужно найти в условиях экономических возможностей, называется целевой функцией или показателем эффективности, или критерием оптимальности. Экономические возможности формализуются в виде системы ограничений. Все это составляет математическую модель задачи. Математическая модель задачи – это отражение оригинала в виде функций, уравнений, неравенств, цифр и т. д. Модель задачи математического программирования включает: 1) совокупность неизвестных величин 2) целевую функцию (она позволяет выбирать наилучший вариант из множества возможных). Её обозначают Z = Z (х). Это может быть прибыль, объем выпуска или реализация продукции, затраты производства, издержки и т. д.; 3) условия (или систему ограничений), налагаемые на неизвестные величины; эти условия могут быть материальные, финансовые, трудовые ресурсы, возможности технического и научного потенциала. Математические ограничения выражаются в виде уравнений и неравенств. Их совокупность образует область допустимых решений (ОДР). Если ОДР обозначим заq, то модель задачи математического программирования примет вид: mах (min) Z = Z ( Илив развернутом виде: найти план Начало математического программирования было положено в 1939 г. советским математиком-экономистом Л. В. Канторовичем. Составными частями математического программирования являются линейное, нелинейное, дискретное, динамическое программирование, а также теория игр и графов.
|
||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 102; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.37.178 (0.009 с.) |

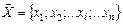 , действуя на которые, систему можно совершенствовать. Её называют планом задачи (вектором управления, решением, стратегией, поведением и т. д.);
, действуя на которые, систему можно совершенствовать. Её называют планом задачи (вектором управления, решением, стратегией, поведением и т. д.);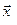 },
}, 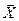 Î Q.
Î Q.


