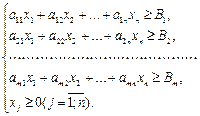Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейное программирование. Общие понятияСодержание книги
Поиск на нашем сайте
Линейное программирование – это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвестные величины которой наложены линейные ограничения, т. е. в линейном программировании целевая функция – это линейная функция, условия – это линейные уравнения, линейные неравенства и т. д. Таким образом, задачи линейного программирования относятся к задачам на условный экстремум функции. Казалось бы, что для исследования линейной функции многих переменных на условный экстремум достаточно применить хорошо разработанные методы математического анализа. Однако, невозможность их применения показывают простейшие примеры. Пусть необходимо исследовать на экстремум линейную функцию Z = Z (x1; x2;…xn) =
Так как Z – линейная функция, то в общем случае
Построение математических моделей простейших Экономических задач 1. Задача использования сырья Пусть некоторая производственная единица (цех, завод и т. д.), исходя из конъюнктуры рынка, технических возможностей может выпускать п различных видов продукции. Предприятие при их производстве должно ограничиться каким-то количеством различных видов ресурсов (сырье, полуфабрикаты, рабочая сила, оборудование, электроэнергия и т. д.). Пусть их число равно т. Рассмотрим задачу на конкретном примере. Для изготовления двух видов продукции Р1, Р2 используют три вида сырья S1, S2, S3. Запасы сырья, количество единиц продукции, а также величина прибыли, получаемая oт реализации единицы продукции, приведены в табл. 1. Таблица 1
Необходимо составить такой план выпуска продукции, чтобы при ее реализации получить максимальную прибыль. Обозначим через х1 – количество изготовленных единиц продукции Р1, х2 – количество изготовленных единиц продукции Р2. Тогда, учитывая количество единиц сырья, идущих на изготовление единицы продукции, а также запасы сырья, получим систему ограничений: Также на х1 и х2 должно быть наложено ограничение неотрицательности х1 ³ 0, х2 ³ 0. Конечную цель решаемой задачи – получение максимальной прибыли при реализации продукции, выразим как функцию цели Z = 50х1 + 40х2 (руб.). Числа х1, х2 могут быть и дробными, так как в задаче не оговорены условия целочисленности. Итак, мы построили математическую модель задачи использования сырья (ресурсов): найти max значение целевой функции Z = 50 х1 + 40 х2 при ограничениях
Обобщим эту задачу (табл. 2). Таблица 2
Математическая модель задачи Пусть дан план
2. Задача о смесях. В различных отраслях народного хозяйства возникает проблема составления таких рабочих смесей на основе исходных (имеющихся) материалов, которые обеспечивали бы получение конечного продукта. К этой группе задач относятся задачи о выборе диеты, составления рациона в животноводстве, шихты в металлургии, смесей для получения бетона и т. д. Мы остановимся на примере задачи составления рациона. При откорме каждое животное ежедневно должно получить не менее 9 единиц питательного вещества S1, не менее 8 единиц вещества S2 и не менее 12 единиц вещества S3. Для составления рациона используют два вида корма. Содержание количества единиц питательных веществ в 1 кг каждого вида корма и стоимость 1 кг корма приведены в табл. 3. Таблица 3
Необходимо составить дневной рацион нужной питательности, причем затраты на него должны быть min. Для составления математической модели обозначим через x1, x2 – количество килограммов корма соответственно 1 и 2 в дневном рационе:
Цель данной задачи – добиться min затрат на дневной рацион, поэтому общую стоимость рациона можно выразить целевой функцией Z = 4x1 + 6x2. Задачу составления рациона можно обобщить, если предусмотреть в рационе т видов питательных веществ в количестве не менее В i (i =
Помимо этих задач, можно привести примеры задач о раскрое материалов, о размещении заказа, транспортной задачи и т. д.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 94; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.209.178 (0.005 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||

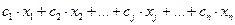 при линейных ограничениях
при линейных ограничениях
 , а, следовательно, внутри области экстремальных точек не существует. Значит, min (mах) значения линейной функции находятся на границе области, которая образована системой ограничений. Для отыскания этих значений потребовалось создание специальных методов. Особенно широкое распространение математическое программирование получило в экономике, так как исследование зависимостей между величинами, встречающимися во многих экономических задачах, приводит к линейной функции с линейными ограничениями.
, а, следовательно, внутри области экстремальных точек не существует. Значит, min (mах) значения линейной функции находятся на границе области, которая образована системой ограничений. Для отыскания этих значений потребовалось создание специальных методов. Особенно широкое распространение математическое программирование получило в экономике, так как исследование зависимостей между величинами, встречающимися во многих экономических задачах, приводит к линейной функции с линейными ограничениями.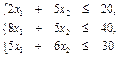 (количество сырья, идущего на изготовление продукции, не должно превышать запасы сырья).
(количество сырья, идущего на изготовление продукции, не должно превышать запасы сырья).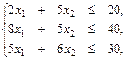
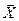 = {x1, x2, … xn} где xj – количество изготовленной единиц j продукции. Тогда требуется найти целевую функцию Z = c1x1 + c2x2 + … + cnxn при ограничениях (условиях):
= {x1, x2, … xn} где xj – количество изготовленной единиц j продукции. Тогда требуется найти целевую функцию Z = c1x1 + c2x2 + … + cnxn при ограничениях (условиях):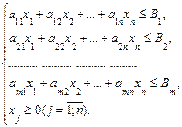
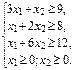
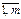 ) и использовать n видов кормов. Обозначим через а ij − количество единиц i-го питательного вещества, содержащего-ся в единице j-го корма, c j − стоимость единицы j корма, x j – количество единиц j-го корма в дневном рационе. Тогда, требуется найти min Z = с1х1 + с2х2 + … + сn хn, при ограничениях:
) и использовать n видов кормов. Обозначим через а ij − количество единиц i-го питательного вещества, содержащего-ся в единице j-го корма, c j − стоимость единицы j корма, x j – количество единиц j-го корма в дневном рационе. Тогда, требуется найти min Z = с1х1 + с2х2 + … + сn хn, при ограничениях: