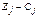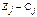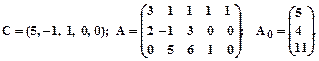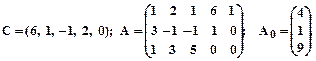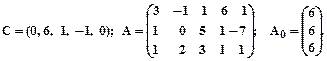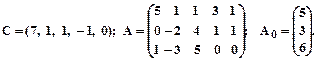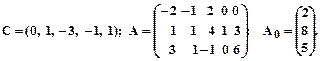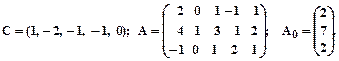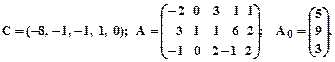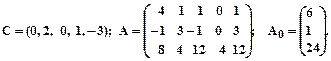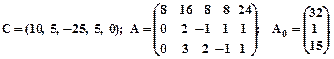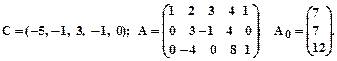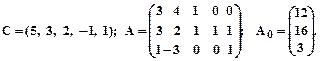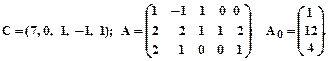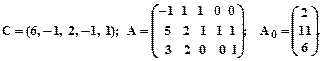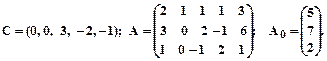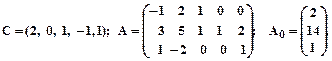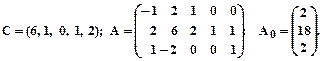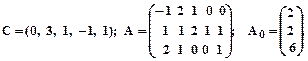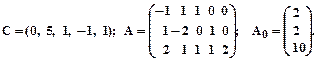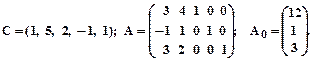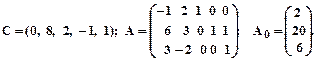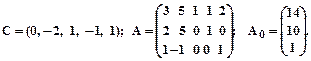Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Симплексный метод решения задач линейного программирования
Доказано, что оптимальное решение задачи линейного программирования связано с угловыми точками многогранника решений, поэтому возникает мысль о следующем пути решения задачи линейного программирования с любым числом переменных. Найти каким-нибудь способом все угловые точки многогранника планов (а их Итак, симплексный метод предполагает: умение находить начальный опорный план, наличие признака оптимальности (неоптимальности) опорного плана, умение переходить к нехудшему опорному плану. 3.1. Построение начального опорного плана 1. Пусть задача линейного программирования представлена целевой функцией Z=c1х1 +с2х2 +...+сnхn = Говорят, что ограничение задачи линейного программирования имеет предпочтительный вид, если в i ³ 0 и левая часть этого ограничения содержит переменную с коэффициентом 1, а в остальные ограничения – равенства она входит с коэффициентом равным 0. Пример 7. Первое и второе ограничения имеют предпочтительный вид, а третье – нет. Если каждое ограничение – равенство задачи линейного программирования имеет предпочтительный вид, то и система ограничений представлена в предпочтительном виде. В этом случае легко найти ее опорное решение: все свободные переменные приравниваются к нулю, тогда базисные переменные равны свободным членам. Пример 8.
а) предпочтительными, т. е. базисными переменными являются х2, х3, х4, а свободными – х1 и х5 б) пусть система ограничений имеет вид
в) в задачах линейного программирования на min (задача о составлении рациона) система ограничений имеет вид В целевую функцию переменные w i вводят с коэффициентом М в случае решения задачи на min и с коэффициентом (– M) для задачи на max, где М – большое положительное число. Полученная задача называется М-задачей, которая соответствует исходной. Она всегда имеет предпочтительный вид. Пусть исходная задача линейного программирования имеет вид: max(min) Z = причем ни одно из ограничений не имеет предпочтительной переменной. Тогда М-задача запишется так: max (min) =
хj ³ 0, (j = Эта система ограничений имеет предпочтительный вид, ее начальный опорный план
Симплексные таблицы. Признак оптимальности опорного плана Итак, любую задачу линейного программирования можно представить в предпочтительном виде: max(min) Z =
хj ³ 0, (j = Рассмотрим эту задачу для n = 4, m = 2 (и распространим ее для общего случая): Z = c1x1 + c2x2 + c3x3 + c4x4.
Выразим базисные переменные (БП) х1, х2 через свободные х3 и х4
x2 =
Введем обозначения в общем виде:
где С учетом этих равенств целевая функция примет вид: max(min)Z= В общем случае задачу записывают в таблицу, которая называется симплексной (табл. 17). Таблица 17
Последнюю строку называют индексной строкой, число Теорема. Пусть исходная задача решается на max. Если для некоторого опорного плана все оценки Δj (j = Доказательство: Так как Z = ΔO Теорема. Если исходная задача решается на min и для некоторого опорного плана все оценки Δj (j = Пример 9. Решить задачу линейного программирования.
Система ограничений задачи имеет предпочтительный вид: базисом являются переменные х2,х4,х1. Заносим условие задачи в симплексную таблицу (табл. 18): Таблица 18
Заполним индексную строку (Z j – с j): ΔO = – 1 × 1,5 – 2 × 2 + 2 × 0,5 = – 4,5, Δ1 = – 1× 0 – 2 × 0 + 2 × 1 – 2 = 0, Δ2 = – 1× 1 – 2×0 + 2×0 – (–1) = 0, Δ3 = – 1× 0,5 – 2 + 2 × (– 0,5) – 3= – 6,5, Δ4 = – 1× 0 – 2×1 + 2×0 – (– 2) = 0, Δ5 = – 1× 0,5 – 2 × 0 + 2 × 0,5 – 1 = – 0,5. Начальный опорный план
3.3. Переход к нехудшему опорному плану Пусть решается задача линейного программирования с системой ограничений в предпочтительном виде
ее начальный опорный план Рассмотрим задачу на mах: если все Δ j ³ 0, то опорный план оптимален. Пусть существует jO, для которого ΔjO < 0. Вектор столбец x i = B I – При значительном увеличении Итак, xjo можно увеличивать до тех пор, пока B i – xjo = min (если это условие выполняется при нескольких i, то в качестве i O можно выбрать любое) Cтроку xm+1 = 0, …,
xm = Новый базис будет состоять из переменных х1, В результате преобразований получен новый опорный план Практика показывает, что в случае решения задачи на max число шагов уменьшается, если разрешающий столбец выбрать по правилу max В случае задачи на min разрешающий столбец нужно выбирать по правилу mах Δj (Δj > 0). Далее процесс повторяется. Проверяем, является ли план Шаг симплексного метода, позволяющий перейти от одного опорного плана к другому нехудшему, называется итерацией.
Симплексные преобразования нового базиса выполняются по правилу: 1. Элементы строки i O новой таблицы равны соответствующим элементам разрешающей строки старой таблицы, деленным на разрешающий элемент: 2. Элементы разрешающего столбца j0 новой таблицы равны 0, за исключением 3. Чтобы найти любой другой элемент новой симплексной таблицы, нужно воспользоваться правилом прямоугольника и полученное число разделить на разрешающий элемент. 4. По 3 пункту вычисляются и элементы индексной строки. Для контроля вычислений они могут быть рассчитаны по формулам Пример 10. Найти max Z = 14х1 – 5х2 + 2х3 – х4 + 8х5, если
Решение. Так как задача имеет предпочтительный вид, то занесем ее условия в симплексную табл. 19 (итерация 0). Таблица 19
0 итерация: исходная задача на max, поэтому начальный опорный план
1 итерация: 1) выбираем разрешающий элемент из условия: max {|Δ1|, |Δ5|} = m a x (4; 1) = 4 – это соответствует 1 столбцу, поэтому его выбираем за разрешающий то есть X1 будем вводить в базис. Для определения разрешающей строки находим минимальное симплексное отношение:
итак, 1 – строка разрешающая =>элемент а11 = 1 – разрешающий; 2) переменную х2 выведем из базиса, а х1 введем в базис; 3) разрешающую строку делим на разрешающий элемент; 4) элементы разрешающего столбца заполняем нулями; 5) остальные элементы пересчитываем по правилу прямоугольника и делим на разрешающий элемент. Делаем контрольные проверки:
Так как существует отрицательная оценка ∆5 = – 5, план 2 итерация: 1) разрешающий столбец 5, переменную. х5,будем вводить в базис. 2) определяем разрешающую строку: min симплексное отношение 3) разрешающую строку делим на 8; 4) в разрешающем столбце проставляем нули; 5) остальные элементы пересчитываем; 6) делаем контрольные проверки, так же как и в итерации 1, так как все Dj ³ 0, опорный план Ответ: Пример 11. Решить М-задачу линейного программирования: Найти: min Z = 3x1 + 2х2 + 3х3, если Решение: Сведем задачу к каноническому виду и введем искусственные переменные
Занесем условие М-задачи в симплексную таблицу (индексную строку записываем в две строки: в первой – слагаемые без М, во второй – слагаемые с М) (табл. 20).
Таблица 20
Окончание табл. 20
Примечание: по мере вывода из базиса искусственных переменных соответствующие им столбцы можно опускать.
Так как все Dj ≤ 0, то план оптимален, Ответ: Замечания: 1. Если в индексной строке последней симплексной таблицы, содержащей оптимальный план, имеется хотя бы одна нулевая оценка, соответствующая свободной переменной, то задача линейного программирования имеет бесконечное множество оптимальных планов. 2. Если в индексной строке симплексной таблицы задачи линейного программирования на max содержится отрицательная оценка Dj < 0, а в соответствующем столбце переменной хj. нет ни одного положительного элемента, то целевая функция на множестве допустимых планов задачи не ограничена сверху. Если же задача линейного программирования на min и в индексной строке содержится положительная оценка Dj > 0, а в столбце переменной хj нет ни одного положительного элемента, то на множестве допустимых планов целевая функция не ограничена снизу. С экономической точки зрения неограниченность целевой функции задачи линейного программирования говорит только об одном; разработанная модель недостаточно точна (бессмысленно говорить о бесконечной прибыли). Типичными ошибками, приводящими к построению моделей такого рода, являются: а) неполный учет ограничений, которые являются существенными в данной задаче; б) небрежные оценки параметров, которые участвуют в ограничениях.
Задания для самостоятельной работы Задание 1. Для изготовления двух видов продукции P1 и P2 используют три вида сырья (S1, S2, S3). На изготовление единицы продукции P1 используют сырье S1 – a1 (ед.), S2 – a2 (ед.), S3 - a3 (ед.). На изготовление единицы продукции P2 используют сырье S1 – b1 (ед.), S2 – b2 (ед.), S3 – b3 (ед.). Запасы сырья S1 составляют не более чем k1, сырья S2 – не более чем k2, сырья S3 – не более чем k3. Прибыль от единицы продукции P1 составляет a руб., от P2 составляет b руб. Необходимо составить такой план выпуска продукции, чтобы при ее реализации получить максимальную прибыль. Данные для выполнения задания соответствующего варианта представлены в табл. 21. Таблица 21
Окончание табл. 21
Заданеи 2. Задана каноническая модель задачи линейного программирования. Z = CX, AX = A0, X ³ 0, A = (aij)3 х 5. Требуется найти max Z М- методом. 1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22. 23.
24.
25.
26.
27.
28.
29.
30.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 171; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.95.38 (0.21 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 =
= 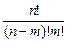 , если каждый план определяется системой m-линейно независимых векторов, содержащихся в данной системе из n векторов Ā1, Ā2 ,..., Ān) и сравнить в них значения целевой функции. Но найти оптимальный план, перебирая все опорные планы задачи трудно, поэтому необходимо иметь схему, позволяющую переходить к не худшему опорному плану и иметь признак того, что лучших крайних точек, чем данная крайняя точка нет. В этом и состоит идея наиболее широко применяемого в настоящее время симплексного метода (метода последовательного улучшения плана).
, если каждый план определяется системой m-линейно независимых векторов, содержащихся в данной системе из n векторов Ā1, Ā2 ,..., Ān) и сравнить в них значения целевой функции. Но найти оптимальный план, перебирая все опорные планы задачи трудно, поэтому необходимо иметь схему, позволяющую переходить к не худшему опорному плану и иметь признак того, что лучших крайних точек, чем данная крайняя точка нет. В этом и состоит идея наиболее широко применяемого в настоящее время симплексного метода (метода последовательного улучшения плана).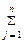 сjхj и системой ограничений, заданной в каноническом виде
сjхj и системой ограничений, заданной в каноническом виде 
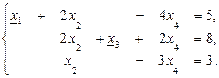
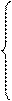
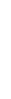

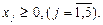
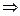 х1 = 0, х5 = 0, а х2 = 10, х3 = 0, х4 = 2. Тогда начальный опорный план
х1 = 0, х5 = 0, а х2 = 10, х3 = 0, х4 = 2. Тогда начальный опорный план  =(0; 10; 80; 32; 0) – угловая точка (согласно теореме 1).
=(0; 10; 80; 32; 0) – угловая точка (согласно теореме 1).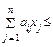 в i; в i ³ 0 (i =
в i; в i ³ 0 (i = 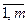 ) в задаче линейного программирования на max (задача об использовании сырья). Сведем задачу к каноническому виду, для этого добавим к левым частям неравенств дополнительные переменные хn + i ³ 0 (i =
) в задаче линейного программирования на max (задача об использовании сырья). Сведем задачу к каноническому виду, для этого добавим к левым частям неравенств дополнительные переменные хn + i ³ 0 (i =  в i; в i ³ 0 (i =
в i; в i ³ 0 (i = 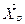 = (0,...0, в1, в2,…, вm) (так как в этой системе все дополнительные переменные будут базисными, а в целевую функцию дополнительные переменные входят с коэффициентом равным 0), то Z = c1x1 + c2x2 + … cnxn + 0×xn+1 + …0×xn+m.
= (0,...0, в1, в2,…, вm) (так как в этой системе все дополнительные переменные будут базисными, а в целевую функцию дополнительные переменные входят с коэффициентом равным 0), то Z = c1x1 + c2x2 + … cnxn + 0×xn+1 + …0×xn+m. в i; в i ³ 0, (i =
в i; в i ³ 0, (i = 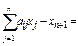 в i; в i ³ 0, (i =
в i; в i ³ 0, (i =  ,
, 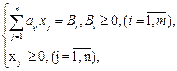
 – (+)
– (+) 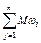 ,
,
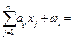 в i,(i =
в i,(i = 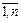 ), w i ³ 0, (i =
), w i ³ 0, (i = 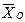 = (0,...0, в1, в2, …, вm). Если некоторые из уравнений исходной системы ограничений имеют предпочтительный вид, то в них не следует вводить искусственные переменные. Итак, если в оптимальном плане
= (0,...0, в1, в2, …, вm). Если некоторые из уравнений исходной системы ограничений имеют предпочтительный вид, то в них не следует вводить искусственные переменные. Итак, если в оптимальном плане  = (х1, x2,.., xn, w1, w2,.., wm) М-задачи все искусственные переменные wI = 0 (i =
= (х1, x2,.., xn, w1, w2,.., wm) М-задачи все искусственные переменные wI = 0 (i = 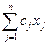 ,
,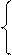 xi +
xi + 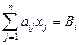 , Bi ³ 0, (i =
, Bi ³ 0, (i = 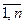 ).
).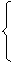
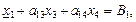
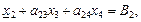
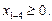
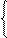 x1 =
x1 = 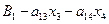 ,
,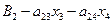 и подставим их в целевую функцию
и подставим их в целевую функцию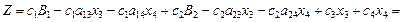
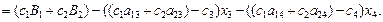
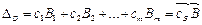 ,
,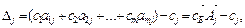
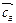 = (с1; с2; …; сm) – вектор коэффициентов целевой функции при базисных переменных,
= (с1; с2; …; сm) – вектор коэффициентов целевой функции при базисных переменных, 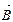 = (B1; B2;..; Bm) – вектор свободных членов;
= (B1; B2;..; Bm) – вектор свободных членов; 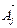 =
= 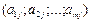 – вектор коэффициентов при переменных х j.
– вектор коэффициентов при переменных х j.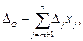 где
где 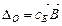 ;
; 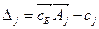
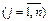 .
.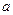 1, m+1 …
1, m+1 … 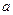 1n
0 1 … 0 … 0
1n
0 1 … 0 … 0 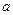 2, j …
2, j … 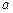 m, m+1 …
m, m+1 … 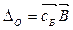 – значение целевой функции для начального опорного плана
– значение целевой функции для начального опорного плана 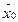 , т. е. ΔO = Z(
, т. е. ΔO = Z(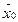 ) =
) = 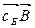 , числа
, числа 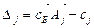 – называются оценками свободных переменных.
– называются оценками свободных переменных.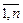 ) не отрицательны (больше или равны 0), то такой план оптимален.
) не отрицательны (больше или равны 0), то такой план оптимален.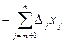 и Δj ³ 0, то Z достигает max, когда
и Δj ³ 0, то Z достигает max, когда 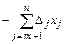 = 0, а это возможно, если хm+1 = 0, хm+2 = 0,..., хn = 0, т. е. опорный план (В1, В2, …, Вm, 0, …, 0) – оптимален.
= 0, а это возможно, если хm+1 = 0, хm+2 = 0,..., хn = 0, т. е. опорный план (В1, В2, …, Вm, 0, …, 0) – оптимален.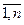 ) не положительны (меньше или равны 0), то такой план оптимален.
) не положительны (меньше или равны 0), то такой план оптимален.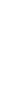
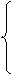
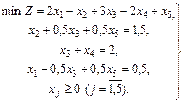 =>
=>
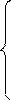
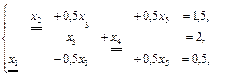
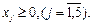
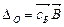 ,
, 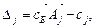
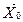 = (0,5; 1,5; 0;2; 0), Z (
= (0,5; 1,5; 0;2; 0), Z (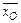 ) = – 4,5. Так как все оценки индексной строки Δ j не положительны, а задача на min, то план
) = – 4,5. Так как все оценки индексной строки Δ j не положительны, а задача на min, то план 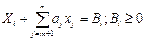 (i =
(i = 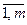 ), (5)
), (5)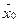 = (В1, В2, …, Вm, 0, …, 0). Значение целевой функции Z(
= (В1, В2, …, Вm, 0, …, 0). Значение целевой функции Z(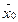 ) =
) = 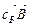 = ΔO.
= ΔO.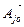 , для которого ΔjO < 0, называется разрешающим, а соответствующая переменная xjo – перспективной. Попытаемся, не изменяя нулевых значений свободных переменных хm+1, хm+2, …, хn, кроме xjo увеличить значение целевой функции Z за счет увеличения переменной xjo > 0. Однако увеличивать xjo надо осторожно, так как выбор
, для которого ΔjO < 0, называется разрешающим, а соответствующая переменная xjo – перспективной. Попытаемся, не изменяя нулевых значений свободных переменных хm+1, хm+2, …, хn, кроме xjo увеличить значение целевой функции Z за счет увеличения переменной xjo > 0. Однако увеличивать xjo надо осторожно, так как выбор 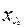 влияет на значения х1,..., хm, которые должны быть ³ 0. Имеем: х1 ³ 0, х2 ³ 0,..., хm ³ 0, хm+1 = 0,..., xjo-1 = 0, xjo > 0, xjo+1 = 0,..., xn = 0 и из (5) имеем
влияет на значения х1,..., хm, которые должны быть ³ 0. Имеем: х1 ³ 0, х2 ³ 0,..., хm ³ 0, хm+1 = 0,..., xjo-1 = 0, xjo > 0, xjo+1 = 0,..., xn = 0 и из (5) имеем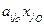 – (i =
– (i = 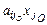 , значит получим хi < 0, что недопустимо. В случае, если
, значит получим хi < 0, что недопустимо. В случае, если 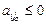 (i =
(i = 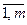 ), такого нарушения не произойдет.
), такого нарушения не произойдет.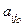 xjo ³ 0, не нарушая общности, можно считать
xjo ³ 0, не нарушая общности, можно считать 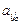 > 0, тогда
> 0, тогда 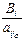 . Найдем среди отношений
. Найдем среди отношений 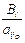 наименьшее. Пусть оно называется наименьшим симплексным отношением и обозначается Q.
наименьшее. Пусть оно называется наименьшим симплексным отношением и обозначается Q.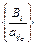 =
= 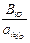 = Q,
= Q,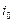 называют разрешающей, элемент
называют разрешающей, элемент 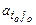 – разрешающим. Переменная
– разрешающим. Переменная 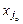 , присутствующая в базисе, является неперспективной и ее выводят из базиса:
, присутствующая в базисе, является неперспективной и ее выводят из базиса: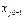 = 0,
= 0, 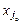 = Q,
= Q,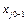 = 0, …, xn = 0, а из равенства (6) находим: x1 = B1 –
= 0, …, xn = 0, а из равенства (6) находим: x1 = B1 – 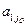 Q, …,
Q, …,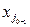 =
= 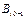 –
– 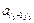 Q,
Q, 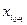 =
= 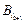 –
– 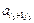 Q, …,
Q, …,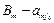 Q.
Q.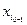 ,..., xm, а соответствующий ему опорный план примет вид, X1 = (B1 –
,..., xm, а соответствующий ему опорный план примет вид, X1 = (B1 – 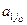 Q; B2 –
Q; B2 – 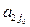 Q; …;
Q; …; 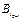 –
– 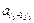 Q; 0;
Q; 0; 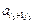 Q; …;
Q; …; 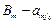 Q; 0; …; Q; 0; …; 0).
Q; 0; …; Q; 0; …; 0).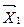 , в котором переменная
, в котором переменная 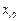 заменена на
заменена на 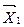 не хуже начального
не хуже начального 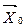 .
.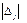 (Δj £ 0), т. е. в базис вводить переменную, которой соответствует max по абсолютной величине оценки.
(Δj £ 0), т. е. в базис вводить переменную, которой соответствует max по абсолютной величине оценки.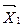 оптимальным, если да, то задача решена. Если нет, то переходим к нехудшему опорному плану
оптимальным, если да, то задача решена. Если нет, то переходим к нехудшему опорному плану 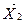 и т. д.
и т. д.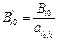 ,
, 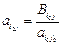 , (j =
, (j = 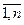 ).
).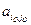 = 1.
= 1.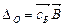 ,
, 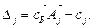
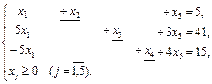
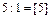
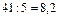
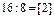
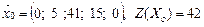 . Он неоптимальный, так как Δ1 < 0, Δ5 < 0.
. Он неоптимальный, так как Δ1 < 0, Δ5 < 0.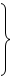
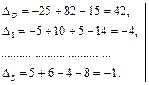
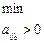
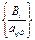 =
= 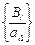 =
= 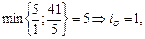
 14 – 5 + 2×16 – 1× 40 = 62;
14 – 5 + 2×16 – 1× 40 = 62; 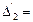 14 – 10 – 5 + 5 = 4;
14 – 10 – 5 + 5 = 4;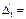 14 + 0 + 0 – 14 = 0;
14 + 0 + 0 – 14 = 0; 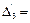 0 + 2 + 0 – 2 = 0;
0 + 2 + 0 – 2 = 0;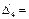 0 + 0 – 1 + 1 = 0;
0 + 0 – 1 + 1 = 0; 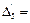 – 14 + 16 + 1 – 8 = – 5 < 0.
– 14 + 16 + 1 – 8 = – 5 < 0. = (5; 0; 16; 40; 0) не оптимальный, Z(x1) = 62 > Z (
= (5; 0; 16; 40; 0) не оптимальный, Z(x1) = 62 > Z (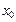 ) = 42.
) = 42.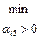
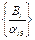 =
= 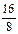 = 2 соответствует 2-ой строке, значит переменную х3 выводим из базиса. Разрешающий элемент а25 = 8;
= 2 соответствует 2-ой строке, значит переменную х3 выводим из базиса. Разрешающий элемент а25 = 8;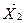 – оптимален
– оптимален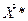 = (7; 0; 0; 42; 2), Z(
= (7; 0; 0; 42; 2), Z(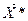 ) = 72.
) = 72.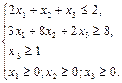
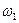 и
и 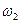 :
:
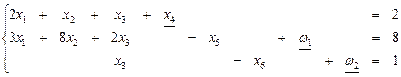
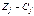
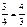 1/
1/ 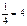 1/1=[1]
1/1=[1]