
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Чистые и смешанные стратегии и их свойства
Различают стратегии чистые и смешанные. А. Чистая стратегия Аi(i = Если игрок А имеет m-стратегий, а игрок В – n-стратегий, то для любой пары стратегий игроков А и В чистые стратегии можно представить в виде единичных векторов, например: для пары стратегий А1, В2 чистые стратегии первого и второго игроков запишутся в виде: для стратегии A1; для стратегии В2; g2 = (0; 1; 0; …; 0). Для пары стратегий Аi, Вj чистые стратегии можно записать в виде: для стратегии Аi; pi = (0;...; 0; 1; 0; …; 0) |® i-место; для стратегии |® j-место. Теорема. В матричной игре нижняя чистая цена меньше или равна верхней чистой цене игры, т. е., α £ b. Доказательство. Возьмем i – строку и j – столбец. По определению a i = min a ij, £ aij, а b j = max a ij ³ a ij Þ a i £ a ij, £ bj Þ a i £ b i, j i (i = Итак как это справедливо для любого i и j, то, следовательно a £ b. Если для чистых стратегий Аi, Вj игроков А и В имеет место равенство a = b, то пару чистых стратегий (Аi, Вj) называют седловой точкой матричной игры, элемент a ij – седловым элементом платежной матрицы, а число u = a = b – чистой ценой игры. Пример 21. Найти нижнюю и верхнюю чистые цены, устано-вить наличие седловых точек матричной игры Решение. Определим нижние и верхние чистые цены игры, для этого составим платежную матрицу,
а седловой элемент равен а12 = 5, этот элемент является наименьшим в первой строке и наибольшим во втором столбце. Если в матричной игре есть седловой элемент, то наилучшими для игроков являются их максиминные и минимаксные стратегии, и эти чистые стратегии, образующие седловую точку – есть оптимальные чистые стратегии. Отклонение игрока А от maxmin стратегии А1 ведет к уменьшению его выигрыша, а отклонение игрока В от минимаксной стратегии ведет к увеличению его проигрыша. Б. Смешанные стратегии. Если же матричная игра не имеет седловой точки, то решение игры затрудняется. В этих играх a < b. Применение минимаксных стратегий в таких играх приводит к тому, что для каждого из игроков выигрыш £ a, а проигрыш ³ b. Для каждого игрока возникает вопрос увеличения своего выигрыша. Решение находят, применяя смешанные стратегии.
Смешанной стратегией игрока А (В) называется вектор
Вектор
Функция Стратегии Использование в игре оптимальных смешанных стратегий обеспечивает игроку А выигрыш не меньший, чем при использовании им любой другой стратегии р, а 2-му игроку – проигрыш не больший, чем при использовании им любой другой стратегии. Совокупность оптимальных стратегий и цены игры составляет решение игры. Цена игры В. Свойства смешанных стратегий. 1. Для того чтобы смешанные стратегии p*=(p1*, p2*, …, pm*) и g* = (g1*, g2*, …, gn*) были оптимальными, для игроков А и B с ценой игры u должны выполняться неравенства:
2. Решение матричной игры можно упростить, выяснив при этом доминирование одних стратегий над другими. Рассмотрим стратегии игрока А, для этого сравним элементы строк s и t: а) если все б) игрок В заинтересован в минимизации проигрыша поэтому доминирующим будет столбец с меньшими элементами; в) в матричной игре строки (столбцы) с одними и теми же элементами называются дублирующими. Доминируемые и дублирующие строки (столбцы) можно опускать, т. к. это не влияет на решение игры.
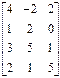
3. Платежную матрицу можно преобразовать в матрицу с положительными числами, умножив все элементы матрицы на какое-либо число b или прибавив к ним какое-либо число с, то есть получив матрицу (b · aij + c) m × n. Пример 22. Выполнить всевозможные упрощения матричной игры
Решение: а) поскольку соответствующие элементы второй и четвертой строк матрицы равны, то есть имеем две дублирующие строки, то опустим, например, четвертую строку. Получим
б) сравним соответствующие элементы строк и столбцов: элементы первого столбца доминируют (<) над элементами третьего и шестого столбцов, то есть игроку В невыгодно применять стратегии В3 и В6. Вычеркнем их. Элементы второго столбца доминируют (<) над элементами четвертого столбца. Опустим его. Получим:
в) элементы 2 строки меньше соответствующих элементов 3-й строки, т. е. 3-я строка доминирует над 2-й строкой (поэтому 2-ю строку опускаем) Þ г) если требуется получить матрицу с положительными членами, то достаточно прибавить к ее элементам, например число с = 3. Получаем:
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 170; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.43.140 (0.007 с.) |
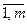 ) игрока А (чистая стратегия Bj (j =
) игрока А (чистая стратегия Bj (j = 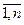 ) игрока В) – это возможный ход игрока А (в), выбранный им с вероятностью, равной 1.
) игрока В) – это возможный ход игрока А (в), выбранный им с вероятностью, равной 1.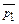 = (1; 0;..; 0);
= (1; 0;..; 0);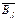 ; gj = (0,..., 0; 1; 0; …; 0)
; gj = (0,..., 0; 1; 0; …; 0)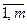 , j =
, j = 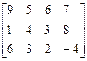 .
.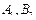 ),
),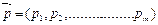 , где
, где  и
и 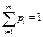
 где
где 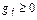
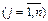 ,
, 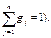
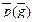 означает вероятность применения i -ой чистой стратегии игроком А (j -ой чистой стратегии игроком В). Так как игроки выбирают свои стратегии случайно и независимо друг от друга, то величина выигрыша (проигрыша) есть случайная величина. Ее средняя величина – математическое ожидание – является функцией от смешанных стратегий
означает вероятность применения i -ой чистой стратегии игроком А (j -ой чистой стратегии игроком В). Так как игроки выбирают свои стратегии случайно и независимо друг от друга, то величина выигрыша (проигрыша) есть случайная величина. Ее средняя величина – математическое ожидание – является функцией от смешанных стратегий 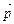 и
и 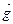 :
: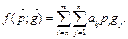
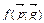 – называется платежной функцией игры.
– называется платежной функцией игры.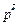 = ('р1*,..., рm*,),
= ('р1*,..., рm*,), 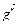 = (g1*, …, gn*) называются оптимальными, если для произвольных стратегий
= (g1*, …, gn*) называются оптимальными, если для произвольных стратегий 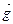 = (g1, g2, …, gm) выполняется условие
= (g1, g2, …, gm) выполняется условие 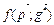 £
£ 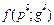 £
£ 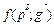 .
.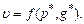 Чистые стратегии игрока, входящие в его оптимальную смешанную стратегию с вероятностями неравными 0, называются активными стратегиями игрока.
Чистые стратегии игрока, входящие в его оптимальную смешанную стратегию с вероятностями неравными 0, называются активными стратегиями игрока.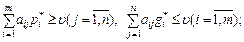
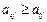 , то выигрыш игрока стратегии Аs будет больше, чем при стратегии Аt, тогда стратегия Аs называется доминирующей, а стратегия Аt – доминируемой;
, то выигрыш игрока стратегии Аs будет больше, чем при стратегии Аt, тогда стратегия Аs называется доминирующей, а стратегия Аt – доминируемой;

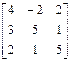 .
.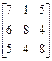 .
.


