
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закрытая и открытая модели транспортной задачиСодержание книги
Поиск на нашем сайте
Модель транспортной задачи называется закрытой, если суммарный объем груза, имеющийся у поставщиков равен суммарно-му спросу потребителей, т. е. выполняется равенство
то модель задачи называется открытой. Для того чтобы решить транспортную задачу с открытой моделью, надо преобразовать ее в закрытую. Если дано условие (7.1), то необходимо ввести фиктивный (n + 1) пункт назначения Вn+1, т. е в матрице задачи вводится дополнительный столбец. Спрос фиктивного потребителя полага-ют равным не балансу, т. е. bn+1 = Аналогично, если дано в задаче условие (16): вводится фиктив-ный поставщик Аm+1, запас груза которого равен Аm+1= При преобразовании открытой задачи в закрытую целевая функция не меняется, т. к. все слагаемые, соответствующие дополнительным перевозкам, равны 0. 6.3. Построение исходного опорного плана Построение опорных планов, а также из преобразование будем производить в распределительной таблице. Если переменная Число занятых опорным планом клеток должно быть равно (m + n - 1). 1. Метод северо-западного угла Сущность его состоит в следующем: в распределительной таблице будем распределять груз, начиная с загрузки левой верхней (условно называем северо-западной) клетки (1:1), двигаясь затем от нее по строке вправо или по столбцу вниз. Рассмотрим это правило на примере: составить план перевозок зерна из районов А1, А2, А3, А4 республики, в которых запасы составляют 800, 700, 1000, 500 тыс. ц. на три элеватора В1, В2, В3 мощностью 1000, 1100 и 900 тыс. ц. Затраты на перевозку 1 ц зерна из районов на элеваторы приведены в табл. 30: Таблица 30
Установим характер задачи. Сравнивая:
задача обладает закрытой моделью, поэтому она имеет опорные планы. Не учитывая стоимости перевозки единицы груза, начинаем удовлетворение потребностей первого потребителя (элеватора В1 за счет района А1), предварительно составив распределительную табл. 31. Таблица 31
Для этого сравниваем а1 и b1 (800 < 1000 В районе А2 осталось 700 – 200 = 500 тыс. ц, удовлетворяем элеватор В2 за счет района А2, для этого сравниваем этот остаток с потребностями элеватора В2: 500 < 1100, записываем 500 тыс. ц. в клетку (2; 2), так как запасы района израсходованы полностью, то далее в строке ставим прочерки. Потребности элеватора остались неудовлетворенными, удовлетворяем их за счет района А3: 1100 – 500 = 600 – помещаем в клетку (3; 2), а далее в столбце прочерк. В районе А3 осталось 1000 – 600 = 400 тыс. ц. зерна, его отправляем на элеватор В3, помещаем в клетку (3; 3). Мощность элеватора В3 (900 – 400 = 500 тыс. ц. зерна) догружаем за счет района А4, в котором имеется 500 тыс. ц. зерна, помещаем это число в клетку (4; 3). Получили план перевозок Х0, по которому на элеватор В1 следует поставить 800 тыс. ц зерна из района А1 и 200 тыс. ц зерна из района А2. На В2 – 500 тыс. ц из А2 и 600 тыс. ц из А3. На В3 – 400 тыс. ц из А3 и 500 тыс. ц из А4. Суммарные расходы на перевозку зерна составляют Z(x0) = 2. Метод «минимального элемента» Сущность этого метода состоит в том, что просматривая тарифы в таблице, в 1-ю очередь заполняется клетка с минимальным значением тарифа. При этом в клетку записывают максимально возможное значение поставки. Рассмотрим тот же пример (табл. 32). Таблица 32
Просматриваем тарифы: min тариф в клетке (2; 2), поэтому в эту клетку помещаем х22 = min (700; 1100) = 700; во 2-й строке ставим прочерки, так как запас зерна в районе А2 израсходован. Просматриваем оставшиеся клетки в таблице. Наименьшие тарифы имеют клетки (1; 1) и (3; 2) с11 = с32 = 3. В клетку (1; 1) помещаем х11 = min (800; 1000) = 800, а в клетку (3; 2) – х32 = min(1000; 1100 – 700) = 400. В первой строке и во 2-м столбце ставим прочерки. Просматриваем тарифы в оставшихся клетках: наименьший тариф в клетке (3; 1). Загружаем ее х31= min (1000 – 800; 1000 – 400) = 200. В первом столбце ставим прочерки, т. к. его мощность В1 использована полностью. Смотрим тарифы далее. Наименьший в клетке (3; 3). Загружаем ее: х33 = min(1000 – 200 – 400; 900) = 400. Загружаем клетку (4; 3): х43 = min(900 – 400; 500) = 500. Получили план Х0, для которого Z(Х0) = 3 · 800 + 2 · 700 + 4 · 200 + 3 · 400 + 5 · 400 + 7 · 500 = 11300 тыс. руб. 6.4. Метод потенциалов решения транспортной задачи, признак оптимальности опорных планов 1. Теорема о потенциалах: Если план Х*= Из теоремы вытекает, что для получения оптимального плана транспортной задачи необходимо выполнение следующих условий: 1) каждой занятой клетке распределительной таблицы соответствует сумма потенциалов, равная тарифу этой клетки, то есть
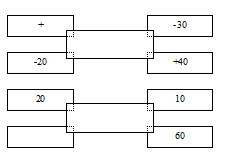
2) каждой свободной клетке соответствует Так как всех занятых клеток должно быть m + n – 1; то следует решить систему m + n – 1 уравнений Для исследования плана на оптимальность для каждой свободной клетки проверяется условие Если хотя бы одна свободная клетка не удовлетворяет данному условию, то опорный план не является оптимальным, его можно улучшить за счет загрузки этой клетки. Если таких клеток несколько, то наиболее перспективной для загрузки является клетка, для которой разность (оценка) между тарифом клетки и суммой её потенциалов наименьшая, то есть Пример 25. Пусть для клеток (i; к) и (i; t) имеем оценки, Sik = = – 5; Sit= – 10. Наиболее потенциальной является клетка (i, t). Если для всех свободных клеток оценки Sit ≥ 0, то опорный план перевозок оптимален. 2. Если для опорного плана перевозок указанное условие оптимальности не выполняется, то за счет загрузки перспективной свободной клетки строится замкнутый цикл с вершинами в загруженных клетках. Вершинам этого цикла условно приписываются знаки: свободной клетке «+», а следующей по часовой или против часовой стрелки «–», следующей «+» и так далее. В клетках цикла с «отрицательными» вершинами выбирается наименьшее значение количество груза λ, которое и перемещается по клеткам этого цикла: прибавляется к поставкам в положительных вершинах и вычитается из поставок в отрицательных вершинах (в результате чего баланс цикла не нарушится). Пример 26 (рис. 17).
Рис. 17 В общем случае цикл представляет собой замкнутую ломаную линию, состоящую из звеньев (отрезков), пересекающихся под прямым углом. Каждое звено соединяет две клетки строки (столбца). Цикл включает одну свободную клетку, остальные клетки цикла заняты. В цикле всегда четное число клеток. Если из занятых клеток образуется цикл, то план перевозок не является опорным. Цикл строится только для свободной клетки. Итак сформируем алгоритм решения транспортной задачи методом потенциалов: 1. Построить опорный план по одному из правил: метод северо-западного угла, метод минимального элемента. 2. Вычислить потенциалы поставщиков и потребителей 3. Вычислить оценки Sij для всех свободных клеток по формуле:
Если все Sij ≥ 0, то полученный план – оптимальный, при этом если все Sij > 0, то этот план единственный. Если хотя бы одна оценка Sij = 0, имеем бесчисленное множество оптимальных планов с одним и тем же значением целевой функции. 4. Если хотя бы одна оценка Sij < 0, то план неоптимальный. Переходим к другому плану. Для этого выбираем Пример 27. С трех складов А1, А2, А3, необходимо доставить овощи в пять торговых точек В1, В2, В3, В4, В5. Требуется закрепить склады за торговыми точками так, чтобы общая сумма затрат на перевозку была min. Числовые данные занесены в табл. 33. Таблица 33
Решение: Исходное опорное решение получим, например, по методу «минимального элемента» (табл. 34). Получен опорный вырожденный план, так как число занятых клеток должно быть m + n – 1 = 3 + 5 – 1 = 7, а у нас это число равно 6. В одну из свободных клеток помещаем 0, и считаем ее занятой. Поместим число 0, например, в клетку (1; 2) с наименьшим тарифом. План будет опорным, так как из занятых клеток не образуется циклов. Таблица 34
2. Для определения потенциалов составляем уравнение из заполненных клеток:
Замечание. Потенциалы можно считать и непосредственно по табл. 33, используя только заполненные клетки. Определим оценки свободных клеток: S11 = 7 – (0 + 7) = 0, S13 = 5 – (0 + 6) = –1 < 0, S14 = 4 – (0 + 2) = 2 > 0, S23 = 3 – (– 1 + 6) = – 2 < 0, S25 = 7 – (– 1 + 2) = 6 > 0, S32 = 5 – (– 4 + 3) = 6 > 0, S34 = 6 – (– 4 + 2) = 8 > 0, S35 = 4 – (– 4 + 2) = 6 > 0. Перспективными являются клетки (1; 3) и (2; 3) с оценками S13 = – 1 и S23 = – 2, наиболее потенциальной является клетка (2; 3), так как – 2 < – 1. Строим для клетки (2; 3) цикл непосредственно в таблице. В цикл войдут клетки (2; 3), (2; 1), (3; 1), (3; 3). Наименьшее количество груза, стоящее в вершинах цикла с отрицательным знаком λ = min (10; 90) = 10. В результате смещения λ по циклу получим новый план (табл. 35). Таблица 35
Для нового плана определяем новые потенциалы, используя только заполненные клетки и новые оценки свободных клеток: S11 = 7 – (5 + 0) = 2 > 0; S13 = 5 – (4 + 0) = 1 > 0; S14 = 4 – 2 = 2 > 0; S25 = 7 – 1 = 6 > 0; S32 = 5 – 1 = 4 > 0; S34 = 6 – 0 = 6 > 0; S35 = 4 – 0 = 4 > 0. Оценки всех свободных клеток неотрицательны, значит план оптимальный. Так как все оценки S > 0, то он единственный. Запишем оптимальный план: Х* = min Z = Z(x*) = 2 · 40 + 2 · 80 + 3 · 10 + 1 · 60 + 3 · 20 + 2 · 80 = = 520 тыс. руб.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 152; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.40.234 (0.007 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

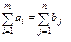 . Если для транспортной задачи выполняется одно из условий:
. Если для транспортной задачи выполняется одно из условий: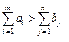 или (15)
или (15)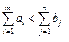 , (16)
, (16)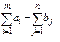 , а все тарифы равными 0, т. е. Сi,n+1 = 0 (
, а все тарифы равными 0, т. е. Сi,n+1 = 0 (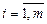 ).
). -
- 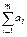 , а тарифы распределительной таблицы равны 0, то есть Сm+1,j = 0 (j =
, а тарифы распределительной таблицы равны 0, то есть Сm+1,j = 0 (j = 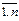 ).
). , то это число записываем в клетку (i, k) и считаем ее занятой (базисной), если же
, то это число записываем в клетку (i, k) и считаем ее занятой (базисной), если же 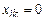 , то клетку (i, k) оставляем свободной.
, то клетку (i, k) оставляем свободной.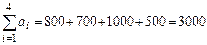 и
и 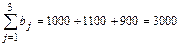 , заключаем, что данная транспортная
, заключаем, что данная транспортная а1 < b1) и записываем в клетку (1; 1) меньшее число 800; запасы района А1 исчерпаны, поэтому остальные клетки 1-й строки прочеркиваем. Потребности элеватора В1 остались неудовлетворенными на 1000 – 800 = 200 тыс. ц. Сравниваем этот остаток с запасами района А2: так как 200 < 700, то помещаем 200 тыс. ц в клетку (2; 1), чем полностью удовлетворяем потребности элеватора В1, а оставшиеся клетки в первом столбце прочеркиваем.
а1 < b1) и записываем в клетку (1; 1) меньшее число 800; запасы района А1 исчерпаны, поэтому остальные клетки 1-й строки прочеркиваем. Потребности элеватора В1 остались неудовлетворенными на 1000 – 800 = 200 тыс. ц. Сравниваем этот остаток с запасами района А2: так как 200 < 700, то помещаем 200 тыс. ц в клетку (2; 1), чем полностью удовлетворяем потребности элеватора В1, а оставшиеся клетки в первом столбце прочеркиваем.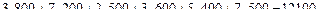 тыс. руб.
тыс. руб. транспортной задачи является оптимальным, то ему соответствует система из (m+n) чисел
транспортной задачи является оптимальным, то ему соответствует система из (m+n) чисел 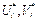 , удовлетворяющих условиям
, удовлетворяющих условиям 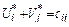 для
для 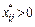 и
и 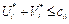 для
для 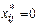
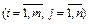 . Числа
. Числа 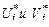 называются потенциалами соответственно i-го поставщика и j-го потребителя.
называются потенциалами соответственно i-го поставщика и j-го потребителя.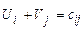 ;
;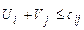 , то есть сумма потенциалов не превышающая тариф этой клетки.
, то есть сумма потенциалов не превышающая тариф этой клетки.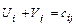 с (m+n) неизвестными. Система неопределенная и, чтобы найти частные решения, одному из потенциалов придаем определенной значение обычно равное 0.
с (m+n) неизвестными. Система неопределенная и, чтобы найти частные решения, одному из потенциалов придаем определенной значение обычно равное 0.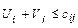 .
.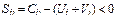 .
.


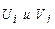 , решив систему уравнений вида
, решив систему уравнений вида 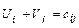 для занятых клеток.
для занятых клеток.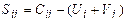 .
.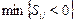 и эта соответствующая клетка будет перспективной. Строим для нее цикл. Получаем новый план. Для нового плана находим потенциалы и т. д.
и эта соответствующая клетка будет перспективной. Строим для нее цикл. Получаем новый план. Для нового плана находим потенциалы и т. д. 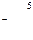
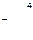
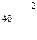

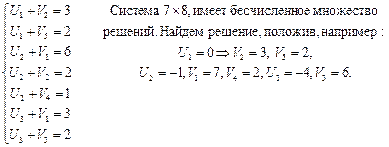
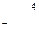
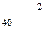
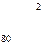
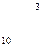
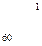
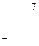
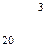
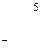
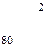
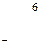
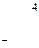
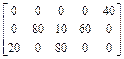 , т. е. со склада А1 надо поставить 40 т овощей в магазин В5, со склада А2 – 80 т в магазин В2, 10 т в магазин В3, 60 т в магазин В4 и со склада А3 20 т в магазин В1, 80 т. в магазин В3. При этом издержки перевозок:
, т. е. со склада А1 надо поставить 40 т овощей в магазин В5, со склада А2 – 80 т в магазин В2, 10 т в магазин В3, 60 т в магазин В4 и со склада А3 20 т в магазин В1, 80 т. в магазин В3. При этом издержки перевозок:


