Матричные игры с нулевой суммой

Теория игр занимается разработкой рекомендаций по принятию ре­шений в конфликтных ситуациях. Математически конфликтную ситуа­цию можно представить как игру двух, трех и более игроков, каждый из кото­рых имеет цель максимизации своего выигрыша за счет другого иг­рока. Иногда теорию игр определяют как раздел математики, изучающий выработку оптимальных правил поведения для каждой стороны, участ­вующей в конфликтной ситуации. Совокупность этих правил называется стратегией.

Под термином игра понимается совокупность предварительно оговоренных правил и условий.

Если n партнеров (игроков) P₁, Р₂,..., Р _n участвуют в данной игре, то основное содержание теории игр состоит в изучении следующей про­блемы: как должен вести партию j -й партнер (j = 1, n) (т. е., что он должен делать, какие правила выполнять) для достижения наиболее благоприятного для себя исхода.

В конце партии предполагается, что каждый игрок P _j получит сумму u _j, называемую выигрышем, причем каждый игрок преследует цель мак­симизации общей суммы выигрыша. Числа u _j могут быть положитель­ными, отрицательными и нулем:

а) если u _j > 0, тогда j -й игрок выиграл;

б) если u _j < 0, тогда j -й игрок проиграл;

в) если u _j = 0, тогда игра имеет ничейный исход.

В большинстве случаев имеем игры с нулевой суммой, т. е. u ₁ + u ₂ +... + u _n = 0. В этих играх сумма выигрыша переходит от одного партнера к другому, не поступая из внешних источников. Игра с нулевой суммой означает, что сумма выигрышей всех игроков в каждой партии равна нулю. В них общая сумма выигрыша перераспределяется между игроками, но не меняется. Примерами игры с нулевой суммой служат многие экономические задачи. В противном случае имеем игру с ненулевой суммой.

Игры, в которых участвуют 2 игрока, называются парными, а игры с большим числом участников – множественными. Принятие игро­ком того или иного решения в процессе игры называется ходом. Ходы могут быть личные и случайные. Если ход выбирается сознательно – это личный ход, иначе – это случайный ход. Игры бывают:

· конечные: каждый из участников имеет конечное число возможных стратегий;

· бесконечные: если хотя бы один из игроков имеет бесконечное число стратегий (ходов);

· бескоалиционные: если игроки не имеют право вступать в соглашения между собой;

· коалиционные: если игроки имеют право вступать в соглашения;

· кооперативные: это игры, в которых заранее определены коалиции.

По виду функций выигрыша игры делятся на: матричные, биматричные, непрерывные, сепарабельные, типа дуэли и т. д.

В дальнейшем мы будем рассматривать матричные игры двух партнеров с нулевой суммой и конечным числом возможных ходов.

Для матричных игр доказано, что любая из них имеет решение и оно может быть легко найдено путем сведения игры к задаче линейного программирования.

Рассмотрим примеры простейших матричных игр.

Пример 17. Шахматы – игра двух партнеров с конечным числом личных ходов.

Пример 18. Игра в «три пальца». Игроки А и В одновременно и независимо друг от друга показывают один, два или три пальца. Размер выигрыша определяется общим количеством показанных пальцев. При этом, если число пальцев четное, то выигрывает игрок А, нечетное – игрок В. Такую игру двух игроков можно представить в виде матрицы

                                              Игрок В

Игрок А

где индекс i указывает количество пальцев игрока А, а индекс j – количество пальцев игрока В. Например, а₁₃ = 4 – выигрыш 4 ед. А, а₃₂ = – 5 – проигрыш 5 ед. А и выигрыш 5 ед. В.

Пример 19. Игрок А выбирает одну из двух сторон монеты, игрок В не зная выбора первого, также выбирает одну из сторон. После того, как оба игрока произвели свой выбор и монета брошена, игрок В платит «1» игроку А, если выбранные стороны монеты совпали, и «(– 1)»,если не совпали, т. е. здесь «1» соответствует выигрышу А (проигрышу В), а «(– 1)» соответствует выигрышу В (проигрышу А), т. е. мы говорим, что А играет на maх, а В – на min.

Задачу можно представить табл. 25:

Таблица 25

	Стратегия игроков	игрок В
		орел	решка
игрок А	орел	1	– 1
	решка	– 1	1

Таким образом, условия игры определяются матрицей

,

строки которой соответствуют стратегиям для игрока А, а столбцы – страте­гиям для игрока В.

Как только А выбирает строку, а В – столбец, партия заканчивается и выигрыш игрока А равен числу, стоящему на пересечении этой строки и столбца. Число а₂₁ = – 1 показывает на проигрыш А и выигрыш В. Это пример матричной игры 2-го порядка.

В общем случае матричная игра задается матрицей, у которой номер i -й строки соответствует номеру стратегии игрока А, а номер j -гo столбца – номеру стратегии игрока В.

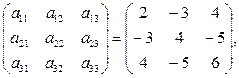
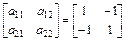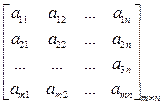
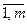Каждый элемент а _ij матрицы является действительным числом и представляет собой сумму выигрыша, уплачиваемую игроком В игроку А, если А выбирает стратегию, соответствующую строке i, а В – столбцу j. Матричную игру записывают в виде табл. 26, называемой платежной матрицей, где A_i = (i = ) – стратегия игрока А, а B_j = (j = 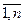) – стратегия игрока В.

Таблица 26