
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двойственный симплексный метод
Воспользуемся (без доказательства) теоремой для решения двойственных задач. Теорема устанавливает связь между оптимальными планами пары двойственных задач. Теорема (теорема двойственности): если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций равны Z(x*) = f(у*). При этом свободным переменным одной задачи сопоставляются базисные переменные другой и наоборот. Пример 15. По условиям примера 1 найти: 1) ассортимент выпускаемой продукции, обеспечивающей предприятию max выручки; 2) оценки ресурсов, используемых при производстве продукции. Решение: 1) Симплексным методом решаем задачу, модель которой уже составлена. Таблица 23
После второй итерации получим все оценки
Основные переменные Дополнительные переменные показывают, что ресурсы Р1 и Р2 используются полностью ( 2) Определимся с переменными В двойственной задаче свободными переменными будут у1, у2, у3, а у4, y5, у6, y7 – базисными переменными. Соответствие между переменными будет:
СП БП
y4 y5 у6 y7 y1 y2 y3
БП СП
Учитывая это соответствие, из индексной строки последней итерации выписываем оптимальный план у*:
В соответствии с основной теоремой двойственности имеем max z (х*) = min f (у*) = 84000. Замечание. Если при решении задачи у нас имеются Затем находим q = max Пример 16. Найти а) m i n Z= -2х1+х2 +5х3 при ограничениях
б) решение двойственной ей задачи. Решение: а) Þ Составим симплексную табл. 24, выбрав за базисные переменные х4 и х5. Так как х5= – 5<0, то просматриваем коэффициенты второй строки. Среди них два отрицательных коэффициента, стоящие в столбцах х1 и х3. Имеем:
Исходная задача решается на отыскание минимального значения линейной функции, поэтому в базис исходной задачи надо включить вектор, которому соответствует
б) решение двойственной задачи:
y3 y4 y5 y1 y2,
БП СП тогда оптимальный план
Задания для самостоятельной работы Задание 1. Составить двойственную задачу для исходной задачи из задания (тема 1, стр. 11). Дать экономическую интерпретацию полученной двойственной задачи. Задание 2. Составить двойственную задачу для исходной задачи из заданий 1 и 2 (тема 2, стр. 26 – 29) и решить ее. Сравнить полученные результаты в двойственной и исходной задаче.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 64; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.127.141 (0.018 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 х5
х6
х7
х5
х6
х7
 1
1
 x6
х7
x6
х7
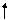 7/4
7/4
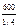 = 2400
= 2400
 = 400
= 400
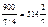
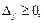 значит найденный опорный план:
значит найденный опорный план: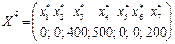 оптимален и
оптимален и 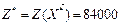 – max.
– max. показывают, что продукцию П1 и П2 выпускать не целесообразно (
показывают, что продукцию П1 и П2 выпускать не целесообразно (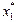 = 0,
= 0, 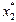 = 0), а продукции П3 произвести
= 0), а продукции П3 произвести  400 ед., продукции П4 –
400 ед., продукции П4 –  500 ед.
500 ед.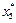 =
=  = 0), а вот ресурса Р3 осталось 200 ед. неиспользованными.
= 0), а вот ресурса Р3 осталось 200 ед. неиспользованными. оптимального плана двойственной задачи: двойственной оценки В прямой задаче х1, х2, х3, х4 являются свободными переменными, а х5, х6, х7 – базисными.
оптимального плана двойственной задачи: двойственной оценки В прямой задаче х1, х2, х3, х4 являются свободными переменными, а х5, х6, х7 – базисными. x1 х2 х3 х4 х5 х6 х7
x1 х2 х3 х4 х5 х6 х7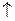

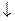



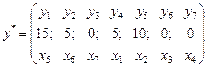 – двойственные оценки.
– двойственные оценки. < 0, то переменную, соответствующую этому свободному члену, следует исключить из базиса. Для выбора переменной, включаемой в ба- зис, просматриваем i-строку: если в ней не содержится
< 0, то переменную, соответствующую этому свободному члену, следует исключить из базиса. Для выбора переменной, включаемой в ба- зис, просматриваем i-строку: если в ней не содержится  , то исходная задача не имеет решения. Если же есть
, то исходная задача не имеет решения. Если же есть 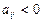 , то для столбцов, содержащих эти
, то для столбцов, содержащих эти 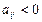 , находим q1 = min
, находим q1 = min 
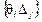 при решении задачи на m i n и q = m in
при решении задачи на m i n и q = m in  при решении задачи на max. Эту переменную и вводим в базис. В процессе вычисления по алгоритму двойственного симплексного метода условие оптимальности (D j ³ 0 или D j £ 0) можно не учитывать, пока не будут исключены все bi < 0, затем оптимальный план находим обычным симплексным методом.
при решении задачи на max. Эту переменную и вводим в базис. В процессе вычисления по алгоритму двойственного симплексного метода условие оптимальности (D j ³ 0 или D j £ 0) можно не учитывать, пока не будут исключены все bi < 0, затем оптимальный план находим обычным симплексным методом.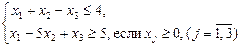

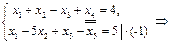
 – система имеет пред- почтительный вид.
– система имеет пред- почтительный вид.
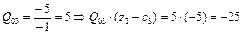
 Таблица 24
Таблица 24
 = = 4
= = 4 = 5
= 5 1
1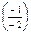 = 0,5
= 0,5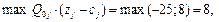 т. е. вектор x1 с разрешающим элементом 1, а x4 исключаем из базиса и т. д. В итоге получаем: план
т. е. вектор x1 с разрешающим элементом 1, а x4 исключаем из базиса и т. д. В итоге получаем: план  = (9/2; 0; 1/2; 0; 0) оптимальный, т. к. все ∆ j = zj – cj £ 0, Z min =
= (9/2; 0; 1/2; 0; 0) оптимальный, т. к. все ∆ j = zj – cj £ 0, Z min =  = –
= – 
 x1 х2 х3 х4 х5
x1 х2 х3 х4 х5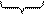

 СП БП
СП БП

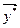 = (– 7/2; – 3/2; 0; – 12; 0), F max = F
= (– 7/2; – 3/2; 0; – 12; 0), F max = F 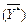 = = – 13/2. Так как все y j ≥ 0, то умножив
= = – 13/2. Так как все y j ≥ 0, то умножив 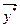 на (– 1), получим
на (– 1), получим


