
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение модели предметной области в виде семантических сетей.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Построение формальной модели предметной области в большинстве случаев является непростой задачей. При построении формальной модели, как правило, используют два принципа: дедуктивный (от общего к частному) и индуктивный (от частного к общему). При дедуктивном подходе рассматривается частный случай общеизвестной фундаментальной модели. Здесь при заданных предположениях известная модель приспосабливается к условиям моделируемого объекта. Индуктивный способ предполагает выдвижение гипотезы, декомпозицию сложного объекта, анализ, затем синтез. Формализованное преставление предметной области в большинстве случаев осуществляется на бумагах и служит основой проекта создания алгоритма программы. В данном случае важным моментом является наглядность, понятность, четкость и общая обозримость модели, что в ряде случаев эффективно реализуется при построении модели предметной области в виде семантических сетей. Для построения предметной области в виде семантической сети рассматриваются основные объекты-сущности данной предметной области и отношения между ними [2]. Первоначально выделяют основные понятия и категории, которыми оперируют (которыми выражаются) фрагменты предметной области. Данные понятия и категории принимаются за первоначальную основу списка объектов-сущностей предметной области. Далее на основе анализа формируются атрибуты, характеризующие выраженные объекты-сущности. При определении перечня атрибутов каждого объекта предметной области, как и самого перечня объектов-сущностей, руководствуются соображениями минимальной достаточности. Часть атрибутов и понятий предметной области выражают процессы-отношения между объектами-сущностями. Такие атрибуты выделяются, и далее анализируются параметры характер связей, которые они выражают - структурность, направленность, множественность, обязательность наличия экземпляров объектов. Чаще всего выделение объектов-сущностей, их атрибутов и отношений-связей осуществляется комбинированным способом на итерационной основе, с многократным уточнением исходного списка объектов, соединением атрибутов в группы и т.д. Распространенным приемом в этом случае является "обобщение" некоторых понятий и атрибутов. Суть обобщения заключается в объединении в одну сущность близких или однотипных понятий, категорий, атрибутов на основе анализа частных проявлений и вариантов [2]. В семантической сети сущности и классы сущностей ассоциируются с узлами, а отношения между сущностями ассоциируются с дугами, соединяющими узлы. Дуга, присоединенная к единственному узлу, устанавливает свойство этого узла. Семантическая сеть позволяет выполнять вывод по цепочкам, описываемым определенными типами дуг [13]. Графические схемы семантических сетей служат удобным способом изображения бинарных отношений и свойств. Поэтому более подходящими для нас будут являться однородные семантические сети со следующими бинарными отношениями: количественные, пространственные, функциональные. В качестве примера можно привести часть семантической сети, относящейся к понятию "птица" (рис. 2) [2]. семантический сеть пролог предметный
Напомним, что семантическая сеть - это способ представления знаний в виде помеченного ориентированного графа, в котором вершины соответствуют понятиям, объектам, действиям, ситуациям или сложным отношениям, а дуги - свойствам или элементарным отношения [19]. С точки зрения структуры, сети являются расширением понятия графа. В информатике под графом понимается конечное множество вершин, соединенных ребрами [19]. В теории графов данное понятие трактуется следующим образом: рассмотрим множество V, состоящее из соединенных некоторым образом точек. Назовем V множеством вершин и элементы v
Число вершин графа G обозначим p, а число ребер - q. В соответствии с геометрическим представлением графа каждая конкретная пара (2) называется ребром графа; вершины а и b называются концевыми точками или граничными точками ребра Е. В определении ребра (2) можно принимать или не принимать во внимание порядок расположения 2-х его концов. Если этот порядок не существенен, то есть если E=(a,b)=(b,a), то говорят, что Е есть неориентированное ребро, если же порядок существенен, то Е называется ориентированным ребром или дугой. В последнем случае, а называется начальной вершиной, а b - конечной вершиной ребра. Также говорят, что Е ребро, выходящее из вершины а и входящее в вершину b. Как в случае ориентированного, так и в случае неориентированного ребра говорят, что ребро Е инцидентно вершинам а и b, а также что а и b инцидентны Е. На рисунке 3 изображено неориентированное ребро (a,b) и ориентированное ребро (c,d). Количество ребер, инцидентных вершине v, называется степенью вершины v и обозначается d(v). Если элементом множества Е является пара одинаковых (не различных) элементов V, то такой элемент множества Е называется петлей, а граф называется графом с петлями (или псевдографом) [15]. Пусть G - неориентированный граф. Маршрутом в G называется такая конечная последовательность ребер Если в маршруте (3) нет ребер, предшествующих Если маршрут S имеет как начальную вершину Маршрут называется цепью, если каждое его ребро встречается в нем не более одного раза (вершины в цепи могут повторяться). Любой участок цепи есть цепь. Нециклическая цепь называется простой цепью, если в ней никакая вершина не повторяется. Ориентированная цепь называется путем. Циклический маршрут называется циклом, если каждое ребро в нем встречается в нем не более одного раза. Цикл с концом Пусть граф G неориентированный. Две вершины a и b называются связными, если существует маршрут вида (3) с концами a и b. Граф называется связным, если любая пара вершин связана [16]. При реализации систем ИИ в настоящее время используются чаще всего переборные методы решения прикладных задач [1]. Для семантических сетей это означает перебор составляющих его вершин и ребер. Следовательно, нам необходимо рассмотреть способы обхода сети из заданной вершины. Если в соответствии с заданными условиями необходимо обработать веса всех вершин, то нам нужно, во-первых, обойти все вершины, а во-вторых, при обходе все вершины должны быть гарантировано посещены по одному разу (гамильтонов цикл). Если же в задаче требуется обработать веса всех ребер, то аналогично необходимо пройти все ребра по одному разу (эйлеров цикл). Не уменьшая общности рассуждений, мы можем рассматривать однородные семантические сети - те, в которых всем ребрам соответствует одно и то же отношение, т.е. одна и та же семантическая функция.
|
||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 450; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.219 (0.008 с.) |



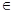 V - вершинами. Граф G=G(V,Е) (1) с множеством вершин V есть некоторое семейство сочетаний или пар вида E=(a,b), a,b
V - вершинами. Граф G=G(V,Е) (1) с множеством вершин V есть некоторое семейство сочетаний или пар вида E=(a,b), a,b  V (2), указывающее, какие вершины считаются соединенными [16].
V (2), указывающее, какие вершины считаются соединенными [16].

 (3) что каждые два соседних ребра
(3) что каждые два соседних ребра  и
и  имеют общую концевую точку. Отметим, что одно и то же ребро Е может встречаться в маршруте несколько раз [16].
имеют общую концевую точку. Отметим, что одно и то же ребро Е может встречаться в маршруте несколько раз [16]. , то
, то 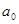 называется начальной вершиной S, а если нет ребер, следующих за
называется начальной вершиной S, а если нет ребер, следующих за  , то
, то  называется конечной вершиной S. Любая вершина,
называется конечной вершиной S. Любая вершина, 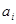 принадлежащая двум соседним ребрам
принадлежащая двум соседним ребрам  и
и  , называется внутренней. Так как ребра и вершины в маршруте могут повторяться, внутренняя вершина может также начальной или конечной вершиной [16].
, называется внутренней. Так как ребра и вершины в маршруте могут повторяться, внутренняя вершина может также начальной или конечной вершиной [16]. , так и конечную вершину
, так и конечную вершину  , то можно написать
, то можно написать  (4) и называть
(4) и называть  , то маршрут называется циклическим [16].
, то маршрут называется циклическим [16]. называется простым циклом, если
называется простым циклом, если 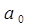 не является в нем промежуточной вершиной и никакие другие вершины не повторяются.
не является в нем промежуточной вершиной и никакие другие вершины не повторяются.


