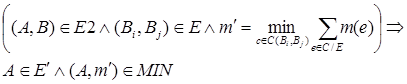Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гамильтонов цикл в однородных семантических сетяхСодержание книги
Поиск на нашем сайте
Рассмотрим задачу теории графов на нахождение гамильтонова цикла в заданном фрагменте графа (сети).
Гамильтоновой цепью в графе называется простая цепь, проходящая через все вершины по одному разу (см. рис) [15]. Простой цикл называется гамильтоновым, если он проходит через каждую вершину графа по одному разу [16]. Теорема (Дирак): Если в графе G(V,E) "vÎV d(v)³p/2, то граф G является гамильтоновым [16]. Рассмотрим классическую задачу теории графов на нахождение гамильтонова цикла - задачу коммивояжера. Она звучит следующим образом: Имеется n городов, расстояния между которыми известны. Коммивояжер должен посетить все n городов по одному разу, вернувшись в тот с которого начал. Требуется найти такой маршрут движения, при котором суммарное пройденное расстояние будет минимальным. Математическая постановка этой задачи состоит в следующем: во взвешенном графе требуется найти гамильтонов цикл наименьшего веса [11]. Данная задача является NP - полной; для нее не существует эффективного алгоритма. Важность этой задачи связана с тем, что к ней сводятся многие другие задачи; в связи, с чем она играет роль эталонной задачи. В данной задаче города, представляя как вершины графа G, в котором каждой паре вершин приписывается расстояние m(a,b). Тогда задача состоит в том, чтобы найти такой гамильтонов цикл P, для которого сумма минимальна.
Проследим ход решения задачи коммивояжера.
Рассмотрим исходный неориентированный граф, где каждому городу соответствует вершины графа, дорогам между ними - ребра. Построим однородную сеть на том же множестве вершин следующим способом: каждому ребру ставим в соответствие две дуги, каждой из которых приписывается вес ребра. Вершина u в орграфе G(V,E) достижима из вершины v, если существует путь из v в u.
Тогда отношение достижимости на взвешенном графе G(V,E) будет транзитивным замыканием E1 на V бинарного отношения E [15]. Построить транзитивное замыкание можно следующим образом: отношения со смежными вершинами принадлежат транзитивному замыканию E1; все отношения с вершинами, достижимыми из смежных вершин, тоже принадлежат замыканию. На языке математической логики это выглядит следующим образом:
где I - тождественное отношение. Введенное таким образом бинарное отношение E1 определяет новую однородную семантическую сеть S1(V,E1,W) с тем же множеством вершин. Заметим, что если граф исходной сети имеет одну компоненту связности, то граф полученной сети будет полным и не будет содержать кратных ребер. Соответствующий граф для данной сети - G1 (см. рис.).
Следующим шагом мы каждому дуге полученного графа G1(V,E1) приписываем множество, состоящее из множеств вершин, пройденных по пути в исходной сети от одной смежной ребру вершины до другой. Обозначим построенное отношение D, DÌE´2V. По определению достижимости существует хотя бы один путь между заданными вершинами в исходном графе, значит это множество не пустое. Можно показать, что существует хотя бы один путь с различными вершинами. Т.к. по определению достижимости: вершина u в орграфе G(V,E) достижима из вершины v, если существует путь из v в u, а путем называется ориентированная цепь. Очевидно, что если есть цепь, соединяющая вершины u и v, то есть и простая цепь, соединяющая эти вершины [15]. Предложение: Для сети S1(V,E1,W,D) вес дуги, составляющий множество, состоящее из множества пройденных вершин, которое мы строим, содержит хотя бы одно множество различных вершин и его мощность не превосходит мощности множества вершин сети |V|. Опираясь на предложение, мы для каждого такого множества, составляющего вес дуги e в S1, можем указать ненулевой максимум мощностей составных множеств из различных вершин. Для этого возьмем подмножество CÌD: D((X,Y))<=|V|. Согласно предложению оно соответствует множеству всех простых цепей из вершины X в вершину Y. Для множества C каждой цепи ставится в соответствие количество вершин в данной цепи Построим сеть S2(V,E1,W,M) на основании G1, приписывая каждому дуге полученный ненулевой максимум. Обозначим этот максимум для данного ребра M(e). Утверждение 1: Если дуга e сети S2, такая что M(e)=|V|, то между вершинами смежными с e существует гамильтонова цепь. Доказательство: По построению данной дуге e мы приписываем ненулевой максимум мощностей множеств вершин в цепях (путях с различными промежуточными вершинами) из одной вершины, смежной дуге е, в другую. Если этот максимум равен мощности множества вершин, то существует хотя бы одна цепь из одной указанной вершины в другую, в которую входят все вершины. Так как все вершины различны, то данная цепь является гамильтоновой цепью. ▲
Строим сеть S3(V,E2,W), где (vi, vj)ÎE2 тогда и только тогда, когда (vi, vj)ÎE1 и в сети S2 вес этой дуги равен |V|. Согласно утверждению 1 граф сети S3, будет отражать отношение существования гамильтоновой цепи в графе исходной сети S. На языке математической логики отношение существования гамильтоновой цепи будет выглядеть следующим образом:
Утверждение 2: Если в графе G(V,E) между вершинами X и Y существует гамильтонова цепь, то она не содержит смежного ребра (X,Y). Доказательство: По условию в графе G(V,E) существует гамильтонова цепь H={(X,V0),(V0,V1),…,(VN-1,VN),(VN,Y)}, |H|=|V|. Предположим, что в этом множестве присутствует смежная дуга (X,Y). Тогда имеется 3 возможности: 1. V0=Y ® получаем дугу; 2. VN=X ® получаем дугу; 3. если Vi и Vj смежные вершины и Vi=X, а Vj=Y, то видим, что вершины X и Y встречаются в цепи не по одному разу, что противоречит определению гамильтоновой цепи. Данное противоречие доказывает истинность утверждения.▲ Следствие: Если в графе G(V,E) между смежными вершинами существует гамильтонова цепь, то есть возможность в данном графе построить гамильтонов цикл. Для этого достаточно дополнить гамильтонову цепь смежной дугой. Теперь для каждой вершины мы можем ввести свойство На языке математической логики это свойство будет выглядеть следующим образом:
Если ввести следующие обозначения: C/E - цепь, состоящая из множества дуг; с - простая цепь из одной вершины в другую; m(e) - вес дуги e, то получим следующее утверждение:
|
||||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 467; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.239.70 (0.007 с.) |









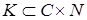 .
.
 существования из нее хотя бы одного гамильтонова цикла. Припишем каждой вершине, имеющей свойство
существования из нее хотя бы одного гамильтонова цикла. Припишем каждой вершине, имеющей свойство  , вес
, вес  - минимум сумм весов дуг, пройденных в каждом из гамильтоновых циклов, начинающихся в заданной вершине. Собственно это и требуется найти по условию задачи. Остальным вершинам приписываем: не определено.
- минимум сумм весов дуг, пройденных в каждом из гамильтоновых циклов, начинающихся в заданной вершине. Собственно это и требуется найти по условию задачи. Остальным вершинам приписываем: не определено. .
.