
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критериальный язык описания выбораСодержание книги
Поиск на нашем сайте
Сложилось несколько языков описания выбора. Самый простой – критериальный язык. Считается, что каждую альтернативу можно оценить конкретным числом (значением критерия) и сравнение альтернатив сводится к сравнению соответствующих им чисел. Пусть х – некоторая альтернатива из множества Х. Считается, что для всех хÎХ может быть задана функция q(х), которая называется критерием (критерием качества, целевой функцией, функцией полезности) и обладает тем свойством, что если альтернатива х1 предпочтительнее альтернативы х2, то q(х1)>q(х2) и обратно. Выбор как максимизация критерия. Если считать, что выбор осуществляется в условиях определенности и заданный критерий q(х) численно выражает оценку последствий этого выбора, то наилучшей альтернативой х* является та, которая обладает наибольшим значением критерия
На практике оценивание любого варианта единственным числом обычно оказывается неприемлемым упрощением. Полное рассмотрение альтернатив приводит к необходимости оценивать их не по одному, а по нескольким критериям, качественно различающимся между собой. Даже в обыденной жизни при выборе мы почти никогда не используем единственный критерий. Итак, пусть для оценивания альтернатив используется несколько критериев qi(x), i=1,2,...p. Теоретически возможно, что на множестве Х окажется одна альтернатива, обладающая наибольшими значениями всех р критериев. Однако, на практике такие случаи почти не встречаются, и возникает вопрос, как же тогда осуществить выбор? Сведение многокритериальной задачи к однокритериальной. Рассмотрим наиболее употребительные способы решения многокритериальных задач. Первый способ состоит в том, чтобы многокритериальную задачу свести к однокритериальной. Это означает введение суперкритерия, т.е. скалярной функции векторного аргумента:
q0(x)=q0(q1(x), q2(x),...,qp(x))
Суперкритерий позволяет упорядочить альтернативы по величине q0, выделив тем самым наилучшую в смысле этого критерия. Вид функции q0 определяется тем, как мы представляем себе вклад каждого критерия в суперкритерий; обычно используют аддитивные или мультипликативные функции:
Коэффициенты si обеспечивают, во-первых, приведение каждого числа к безразмерному виду и, во-вторых, если это необходимо, выполнение условия
Коэффициенты ai и bi – отражают относительный вклад частных критериев в суперкритерий. Итак, при данном способе задача сводится к максимизации суперкритерия
Очевидные достоинства объединения нескольких критериев в один сопровождаются рядом недостатков. Главный недостаток заключается в произвольности выбора весовых коэффициентов ai и bi и, соответственно, произволу получаемому при максимизации. Кроме этого, недостаток одного частного критерия может быть скомпенсирован избыточным значением другого, что часто оказывается неприемлемым. Другой вариант поиска альтернативы, частично свободный от недостатков предыдущего варианта, дает максимизация минимального критерия:
что означает подтягивание самого отстающего. Условная оптимизация. Недостатки свертывания нескольких критериев заставляют искать другие подходы к решению задач многокритериального выбора. Рассмотрим другой метод решения таких задач. Он состоит в том, что выделяется один, главный критерий, а остальные рассматриваются как ограничения. Тогда задача выбора формулируется как задача нахождения условного экстремума основного критерия.
В некоторых задачах оказывается возможным или даже необходимым задавать ограничения на сопутствующие критерии не так жестко, тогда qi(x)£ci. Метод уступок. Иную постановку дает метод уступок. Пусть частные критерии упорядочены в порядке убывания их важности. Возьмем первый из них и найдем лучшую по этому критерию альтернативу. Затем определим «уступку» Dq1, то есть величину, на которую мы согласны уменьшить значение самого важного критерия, чтобы за счет уступки попытаться увеличить, насколько возможно, значение следующего по важности критерия и т.д. Нахождение паретовского множества. Еще один способ многокритериального выбора состоит в отказе от выделения единственной «наилучшей» альтернативы и соглашении о том, что предпочтение одной альтернативе перед другой можно отдавать, только если первая по всем критериям лучше второй. Если же предпочтение хотя бы по одному критерию расходится с предпочтением по другому, то такие альтернативы признаются несравнимыми. В результате попарного сравнения альтернатив все худшие по всем критериям альтернативы отбрасываются, а все оставшиеся несравнимые между собой (недоминируемые) принимаются. Если все максимально достижимые значения частных критериев не относятся к одной и той же альтернативе, то принятые альтернативы образуют множество Парето и выбор на этом заканчивается. Групповой выбор
В человеческой практике единоличное принятие решений является не единственной формой выбора. «Ум – хорошо, а два – лучше» - гласит поговорка, имеющая в виду тот случай, когда оба ума одинаковыми измерениями пытаются найти хороший выбор. Именно такую ситуацию мы и будем здесь рассматривать. Описание группового выбора на языке бинарных отношений. Второй, более общий язык, на котором описывается выбор – это язык бинарных отношений. Дело в том, что в реальности дать оценку отдельно взятой альтернативе часто затруднительно или невозможно, однако, если рассматривать ее не в отдельности, а в паре с другой альтернативой, то находятся основания сказать, какая из них более предпочтительна. Основные предположения языка бинарных отношений сводятся к следующим: 1. Отдельная альтернатива не оценивается, т.е. критериальная функция не вводится. 2. Для каждой пары альтернатив (x,y) некоторым образом можно установить, что одна из их предпочтительнее другой, либо они равноценны (или несравнимы). 3. Отношение предпочтения внутри любой пары альтернатив не зависит от остальных альтернатив, предъявленных к выбору. Математически бинарное отношение R на множестве X определяется как определенное подмножество упорядоченных пар (x,y). Удобно использовать обозначение xRy, если x находится в отношении R с y, и
{(x,y), x,yÎX}
называется полным бинарным отношением. Поскольку в общем случае не все возможные пары (х,у) удовлетворяют условиям, накладываемым отношением R, бинарное отношение является некоторым подмножеством полного бинарного отношения, где RÍX*X. Задать отношение, это значит тем или иным способом указать все пары (х,у), для которых выполнено отношение R. Итак, пусть на множестве альтернатив Х задано n различных индивидуальных предпочтений (бинарных отношений) R1, R2,...,Rn. Ставится задача о выработке некоторого нового отношения R, которое согласует индивидуальные выборы, выражает в каком-то смысле «общее мнение» и принимается за групповой выбор. Очевидно, что это отношение должно быть какой-то функцией индивидуальных выборов
R=F(R1, R2,..., Rn). Различным принципам согласования будут отвечать разные функции F. В принципе эти функции могут быть совершенно произвольными, учитывать не только индивидуальные выборы, но и другие факторы, в том числе и исход некоторых случайных событий (например, бросание жребия). Главный вопрос состоит в том, чтобы правильно отобразить в функции F особенности конкретного варианта реального группового выбора. Например, выборы президента, выборы в Государственную думу и т.д. Различные правила голосования. Один из наиболее распространенных принципов согласования – правило большинства: принятой всеми считается альтернатива, получившая наибольшее число голосов. Правило большинства привлекательно своей простотой и демократичностью, но имеет особенности, требующие осторожного с ним обращения. Прежде всего, оно лишь обобщает индивидуальные предпочтения, а его результат не является критерием истины («выбирают не лучших, а себе подобных»). Во-вторых, даже в простейшем случае выбора одной из двух альтернатив легко представить, когда правило не срабатывает – например, разделение голосов поровну. Кроме того, существует «простое большинство» – 50% +1 голос; «квалифицированное большинство» – 2/3 голосующих – за; принцип консенсуса – 100% - за. При любом из вариантов подразумевается отказ от принятия решения. Поскольку в реальной жизни отказ от дальнейших действий, следующих за принятием решения, недопустим, разрабатываются различные приемы, сокращающие число ситуаций, приводящих к отказу. Парадоксы голосования. Итак, казалось бы, что исключив возможность непринятия решения, например, привлекая трех экспертов, которые большинством голосов выбирают предпочтительную альтернативу, можно решить все проблемы. Однако, здесь мы приходим к еще одной особенности правила голосования – его нетранзитивности. Пусть, например, каждая из трех группировок законодателей, образующих большинство лишь попарно, выдвинула свой вариант законопроекта: a,b,c. Чтобы гарантировать большинство на каждом шаге процедуры, альтернативы предъявляются попарно. Каждая сторона руководствуется при этом своим набором предпочтений: пусть это будут последовательности (a>b>c), (b>c>a), (c>a>b). После голосования по паре (a,b) – получаем 2 голоса против одного: a>b; по паре (b,c) имеем b>c; по паре (a,c) имеем c>a. Голосование большинством не привело таким образом к выяснению «общепризнанного» порядка альтернатив a>b>c>a. В случае применения процедуры, при которой после рассмотрения очередной пары отвергаемая альтернатива заменяется новой, окончательно принятое решение зависит от порядка предъявления альтернатив: при порядке (a,b,c) выбирается c; при порядке (b,c,a) выбирается a; при порядке (a,c,b) выбирается b. Если таким образом принимается законопроект, то чье мнение он будет выражать – большинства или организатора голосования? Очевидно, что такие решения не отвечают идеалу согласованного группового выбора. Задача группового выбора часто все же может быть решена. Особенно, если не считать неприемлемым «диктаторский» принцип согласования. Например, в армии это единственно возможный принцип. В том случае, если использовать единую числовую, а не индивидуальные порядковые шкалы предпочтений, то проблемы нетранзитивности вообще не возникнет.
Рассмотрим еще одну особенность голосования, которую следует иметь в виду на практике. Речь идет о вмешательстве коалиций в механизм голосования, которое фактически меняет его характер. Например, при многоступенчатом голосовании по правилу большинства, коалиция, находящаяся в меньшинстве, может добиться принятия своего решения. На рис. изображено голосование по три большинством в 2/3 на каждой ступени. Видно, что уже на второй ступени меньшинство может навязывать свою волю большинству. Если число ступеней не ограничивать, то теоретически побеждающее таким образом меньшинство может быть сколь угодно малым. То, что при многоступенчатом голосовании может победить претендент, не набравший действительного большинства голосов, происходит и в действительности. Например, в 1876 г. президентом США был избран Р.Б. Хейес (185 голосов выборщиков), а не С. Дж. Тилден (184 голоса), хотя на долю последнего пришлось 51% голосов всех избирателей. Такие же ситуации имели место в президентских выборах 1874, 1888 и 2000 г.г.
|
||||
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 360; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.242.169 (0.008 с.) |


 ;
;  .
. .
.

 ,
,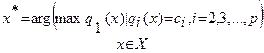
 в противном случае. Множество всех пар
в противном случае. Множество всех пар



