
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні елементи обчислень під час топогеодезичної прив'язки.Содержание книги
Поиск на нашем сайте Основними елементами під час обробки результатів вимірювань в ході топогеодезичної прив'язки являється вирішення прямої, зворотної геодезичної задачі та трикутника. Вирішення прямої геодезичної задачі на площині (рис.20) зводиться до обчислення прямокутних координат точки ( Пряма геодезична задача на обчислювачі СТМ та логарифмічній лінійці розраховується в такому порядку (бланк 1): - записують в бланк координати точки А (для 1;2), відстань АВ (для 3) і дирекційний кут - згідно зі значенням ( - обчислюють приріст координат (для 7 і 8) по формулах: визначають знаки приросту координат згідно рис.19; - обчислюють прямокутні координати точки В (для 9 і 10)
Рисунок 20 - Пряма та обернена геодезична задачі
Бланк 1- Вирішення прямої геодезичної задачі
Обчислення приросту координат на логарифмічній лінійці проводять в такому порядку: - встановлюють початок (кінець) шкали движку проти відстані АВ на шкалі - риску візиру встановлюють на значення куту 15-00-R по шкалі Sin або S и T, залежно від величини куту 15-00-R; - знімають по шкалі - переводять риску візира на величину R і знімають по шкалі
Рисунок 21 - Перехід від дирекційного куту напрямку до куту R і навпаки
Для обчислення приросту координат на обчислювачі СТМ потрібно: - встановиш початок шкал рухомого кола проти відстані АВ на шкалі чисел (шкала 3) основного кола; - індекс движка встановити на величину 15-00-R по шкалі синусів (шкали 4 або 5) і по шкалі 3 проти індексу читають ∆X; - індекс встановити на величину R по шкалі синусів (шкали 4 або 5) і по шкалі 3 проти індексу прочитати ∆Y. Кількість цілих знаків в прирості координат визначають виходячи із такого правила:- якщо 15-00-R (R) по величині 0-95,7 до 15-00, то 0,1 АВ ≤ ∆Х (∆Y) ≤ АВ (20) - якщо 15-00-R (R) по величині від 0-09,5 до 0-95,7, то 0,01 АВ ≤ ∆ Х(∆Y) ≤ 0,1 АВ (21) - якщо 15-00-R (R) по величині від 0-01 до 0-09,5 то 0,001 АВ ≤ ∆X (∆Y) ≤ 0,01 АВ. (22) Вирішення зворотної геодезичної задачі (рис.19) на площині зводиться до обчислення дирекційного кута з даної точки на іншу і відстані між ними по прямокутних координатах цих точок. Вирішення зворотної геодезичної задачі на логарифмічній лінійці і обчислювачі СТМ. (бланк 2) проводиться в такому порядку: 1. Визначають значення приросту координат за формулою: 2. Обчислюють величину куту де: в - менше із приросту координат ∆X або ∆Y; а - більше із приросту координат ∆X або ∆Y;
Обчислення проводяться у такій послідовності:
Примітка. Якщо відхилення більшого приросту до меншого приросту менше 10, відлік знімають зі шкали 1 обчислювача (шкали тангенсів логарифмічної лінійки); якщо ж більше 10, але менше 100, зі шкали 2 обчислювача (шкали 8 і Т логарифмічної лінійки) і зменшують в 10 разів. 3. Обчислюють дирекційний кут 4. Обчислюють відстань АВ (для 9) за формулою: у такій послідовності:
Таблиця 3 - Визначення дирекційного куту цілі через кут
Бланк 2 - Вирішення зворотної геодезичної задачі на обчислювачі СТМ або логарифмічній лінійці
При більш точних розрахунках на логарифмічній лінійці відстань АВ визначають через приріст ∆а більшої різниці координати " а ". Для визначення величини ∆а край шкали движка встановлюють проти величини " в " на шкалі Обчислення відстані при її визначенні за допомогою короткої бази (рис.22) роблять за табл.2 або формулою Д = В / tg
Обчислення проводять в такому порядку:
Кількість цілих знаків у числі визначають виходячи з величини - якщо - якщо Приклад. Обчислити відстань АВ, якщо на одній із точок перпендикулярно напрямку АВ відкладений допоміжний базис В = 45 м, кут АВ = 45 / tg1-27,3 = 336 м.
Рисунок 22 - Визначення відстані за допомогою короткої бази, що розгорнута під прямим кутом
Обчислення горизонтальної відстані (рис.23) по виміряній нахиленій далині проводять по формулі:
Рисунок 23 - Визначення горизонтальної відстані по виміряній нахиленій далині
Обчислення проводять в такому порядку:
Приклад. Обчислити горизонтальну відстань, якщо далина нахилу
Обробку результатів зворотної засічки по дирекційних кутах аналітичним методом проводять у такому порядку: визначать прямокутні координата контурних точок (А і В) вирішенням зворотних геодезичних задач, обчислюють дирекційний кут - змінюють дирекційні кути А = - обчислюють кут - обчислюють відстань від контурних точок до точки, що прив'язується, за формулами: - вирішенням прямих геодезичних задач обчислюють координати точки Р відносно точок А і В. Різниця в координатах не повинна перевищувати 20 м, якщо координати контурних точок взяті з каталога (списку) координат геодезичних мереж, і 50 м, якщо координати визначались по карті масштабом не менше 1:50000. За кінець координати прив'язуємої точки приймають середнє арифметичне значення, якщо різниці в координатах прив'язуваної точки не перевищують допустимих значень.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 411; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.216 (0.009 с.) |

 ), яка визначається, по відомих координатах заданої точки (
), яка визначається, по відомих координатах заданої точки ( 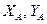 ), відстанню між точкою (АВ) і дирекційному куту з заданої точки на (
), відстанню між точкою (АВ) і дирекційному куту з заданої точки на ( 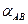 ).
). (18)
(18) . (19)
. (19)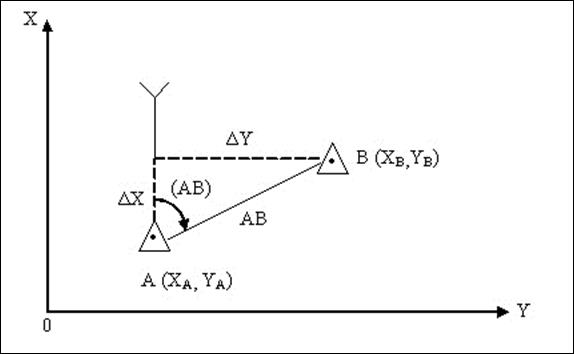

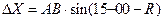
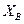



 ;
;
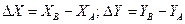 (для 5 і 6) (23)
(для 5 і 6) (23) (для 2) за формулою:
(для 2) за формулою: , (24)
, (24) по шкалі чисел (шкала 6) індекс движку суміщають з початком рухомого кругу і по шкалі тангенсів (шкали 1 і 2) знімають значення кугу
по шкалі чисел (шкала 6) індекс движку суміщають з початком рухомого кругу і по шкалі тангенсів (шкали 1 і 2) знімають значення кугу  (25)
(25)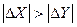







 . (26)
. (26)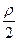 на відповідній шкалі тангенсів і на шкалі
на відповідній шкалі тангенсів і на шкалі 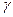 .
.
 . (27)
. (27)
 по шкалі 4 і проти індексу на шкалі 3 знімають далину
по шкалі 4 і проти індексу на шкалі 3 знімають далину
 = 4870 м, а кут місця
= 4870 м, а кут місця  м.
м. і
і 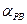 на 30-00 і обчислюють кути А і В:
на 30-00 і обчислюють кути А і В: -
-  ; В=
; В=  -
-  =
=  (29)
(29)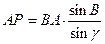 (30)
(30)


