
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахунок однофазних та трифазних електричних кіл з несинусоїдними ЕРССодержание книги
Поиск на нашем сайте Приклад 1. Розкласти в ряд Фур'є криву напруги, зображену на рисунку 2.25. Розв’язування. Для спрощення задачі розбиваємо період тільки на 12 частин (m=12) і визначаємо за графіком значення ординат в точках ділення та їх добутку на
Таблиця 2.1 – Результати розрахунків для першої гармоніки Аналогічну таблицю складаємо для другої гармоніки k=2 (таблиця 2.2).
Таблиця 2.2 – Результати розрахунків для другої гармоніки
Використовуючи дані з таблиці 2.1 та 2.2, визначаємо коефіцієнти:
C1 = 0; B2 = 0; C2 = -22,8. Якщо обмежитись постійною складовою і двома першими гармоніками, то шуканий ряд має вигляд:
u(t)=[31,1+50sinwt-22,8cos2wt] B, або u(t)=[31,1+50sinwt+22,8sin(2wt-900)] B.
Для порівняння наведемо точне значення цих складових ряду Фур’є: u(t)=[31,1+50sinwt+21,2sin(2wt-900)] B. Для розрахунку електричних кіл, ввімкнених на несинусоїдну напругу (not sinusoidal voltage), застосовується метод накладання (superposition method). Кожна гармонічна складова напруги створює свою складову струму. Загальний струм в колі визначається як сума миттєвих значень окремих гармонік струму. Розрахунок кожної гармонічної складової струму проводиться відомими методами у комплексній формі. При цьому необхідно враховувати, що із збільшенням номера гармонік індуктивний опір зростає, а ємнісний зменшується: XLK=kwL; XCK=1/ kwC, де k -номер гармоніки; w- кутова частота (angular frequency) першої гармоніки. Активна потужність, що споживається колом, при несинусоїдних струмах і напругах визначається як сума активних потужностей окремих гармонік: P=U0I0 + U1I1cosj1 + U2I2cosj2 +..., де Uk, Ik - діючі значення напруги і струму k -ї гармоніки; jk - кут зсуву фаз між напругою і струмом k -ї гармоніки. Повна потужність усього кола: S= UI, де U, I - діючі значення несинусоїдних напруг і струмів. Приклад 2. Визначити величину індуктивності L1 (рисунок 2.26), при якій у колі можливий резонанс (resonance) на частоті п’ятої гармоніки (k=5); величину вхідного опору кола при резонансі. Параметри елементів кола: L2=0,01Г; С=10 мкФ; r=50 Ом; f1 =50 Гц.
Розв’язування. Визначимо вхідний опір схеми в комплексній формі:
де хk1 = kwL; xk2 = kwL; xck=1/(kwC); w = 2pf1. Усунемо уявну складову знаменника другої складової, помножимо чисельник і знаменник на спряжений комплексний вираз:
Розділимо праву частину на дійсну і уявну складові:
Дійсна частина цього виразу являє собою вхідний активний опір кола, уявна – вхідний реактивний опір. Щоб коло знаходилось в стані резонансу напруг, необхідно виконати умову:
або
Підставимо числові дані, отримаємо L1=15,9 мГ. Повний вхідний опір всього кола при цьому дорівнює дійсній складовій:
Приклад 3. Розрахунок трифазного кола при дії несинусоїдальної трифазної ЕРС. 1. Знайти миттєве значення напруги U bc. 2. Побудувати графік цієї напруги. 3. Знайти її діюче значення. 4. Знайти активну і повну потужність трифазної системи.
Рисунок 2.27
Перша гармоніка (пряма послідовність)
Реактивні опори:
Фазні струми з’єднання зіркою:
Фазні струми з’єднання трикутником:
Лінійні струми:
Напруга між точками b i c:
Активна потужність приймачів:
Третя гармоніка (нульова послідовність)
Реактивні опори для третьої гармоніки:
Враховуючи, що третя гармоніка створює нульову послідовність фаз, тобто Знайдемо фазні струми в з’єднанні зіркою:
П’ята гармоніка (зворотна послідовність)
Реактивні опори для п’ятої гармоніки:
Напруга між точками b і c:
Графік напруги Ubc(t)
Діюче значення напруги Ubc :
Активна потужність, що споживається трифазним колом:
Рисунок 2.28
Визначаємо повну потужність трифазної системи:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 497; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.93.246 (0.007 с.) |

 і на
і на  . Складаємо таблицю результатів розрахунку для знаходження сталої складової і коефіцієнтів ряду першої гармоніки k=1 (таблиця 2.1)
. Складаємо таблицю результатів розрахунку для знаходження сталої складової і коефіцієнтів ряду першої гармоніки k=1 (таблиця 2.1)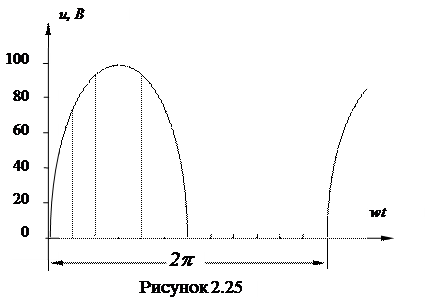






 .
.






 .
.

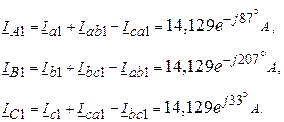
 .
. .
. .
. .
. лінійні напруги будуть відсутні:
лінійні напруги будуть відсутні:  , так само
, так само 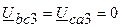 , тоді фазні струми в з’єднанні трикутником також відсутні:
, тоді фазні струми в з’єднанні трикутником також відсутні:  .
.





 .
. .
.




