
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перехідні процеси в лінійних електричних колахСодержание книги
Поиск на нашем сайте
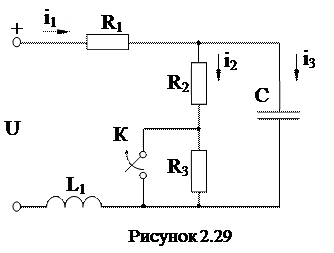
Приклад 1. Класичним методом визначити струми перехідного процесу (transient process) у всіх вітках кола (рисунок 2.29) і напруги на індуктивності і ємності при розмиканні ключа К. Параметри кола: R1=20_Ом, R2=38 Ом, R3=87 Ом, L=0,25 Г, С=100 мкФ, U=290 В. Розв’язування. Вибираємо додатний напрямок струмів в вітках і складаємо рівняння за законами Кірхгофа для післякомутаційного стану кола:
З цієї системи рівнянь, вилучаємо всі невідомі, крім однієї, наприклад uc, отримаємо лінійне диференціальне рівняння (linear differential equation) з одним невідомим. Для цього виразимо невідомі i1, i2, i3 через uc. Струм i3 виражений через uc в останньому рівнянні системи. Із 3-го рівняння системи:
Підставимо значення струмів i2, i3 в перше рівняння системи (1), отримаємо:
Замінивши струми їх значеннями через напругу в другому рівнянні системи, отримаємо:
або
Після перетворень:
Таким чином, знаходження напруги uC зводиться до розв’язування неоднорідного диференціального рівняння (non-homogeneous differential equation) другого порядку. Загальне розв’язування цього рівняння записується у вигляді двох складових (примусової і вільної): uC=uC пр+uC в . Примусову складову визначають з розрахунку нового сталого режиму, тобто при розімкнутому ключі. В цьому режимі в колі протікає постійний струм, який не проходить через ємність, тому
Напруга на ємності в усталеному режимі дорівнює напрузі на опорах R2 i R3, тобто
Вільну складову записують в залежності від виду коренів характеристичного рівняння (characteristic equation):
або
Корені рівняння
Оскільки корені характеристичного рівняння – спряжені комплексні, то вільна складова
де
Спільний вираз для напруги на ємності: uC = 250 + e-80t (A1sin200t + A2cos200t). (5) Для визначення сталих інтегрування використаємо початкові умови. Відповідно до законів комутації (commutation laws) uC(0+) = uC(0-); iL(0+) = iL(0-). Тому знаходимо напругу на ємності і струм в індуктивності до комутації, тобто при замкненому ключі:
Підставимо значення uc(0+) i t = 0 в рівняння (5), отримаємо 190=250+А2 . Звідси А2= -60. Для знаходження А1 використаємо другу початкову умову (starting condition) iL(0+), для чого виразимо струм iL через постійні інтегрування А1 та А2. Підставимо рівняння (5) в формулу (3), отримаємо:
Після підстановки числових значень і деяких перетворень i1=2+e-80t(0,02A1cos200t+1,2sin200t). Підставивши числові значення при 5=2+0,02А1 Звідки А1=150. Таким чином,
uc=[250+e-80t(150sin200t-60cos200t)] В. Знаючи uc, струми в вітках визначають за виразами (1) – (3):
i1=[2+e-80t(1,2sin200t+3cos200t)] A, i2=[2+e-80t(1,2sin200t-0,48cos200t)] A, i3=3,48e-80tcos200t A. Відомо, що a sinwt + b coswt=Asin(wt+g), де tgg=b/a; тому uc=[250+162e-80tsin(200t-21° 50¢)] В; i1=[2+3,23e-80tsin(200t+68° 10¢)] A; i2=[2+1,29e-80tsin(200t+21° 50¢)] A; i3=3,48e-80tsin(200t+90) A. Напруга на індуктивності
Приклад 2. Розрахувати перехідний процес в схемі 5.1 операторним методом. Розв’язування. Запишемо ще раз систему рівнянь, складену за законами Кірхгофа:
Враховуючи, що i1(t)ºI1(s), i2(t)ºI2(s), i3(t)ºI3(s); uc(t)ºUc(s)
Перепишемо цю систему в операторній формі:
Замість диференціальних рівнянь отримали алгебраїчні. Розв’язуємо отриману систему відносно однієї невідомої, наприклад Uc(s):
де i1(0), uc(0) – початкові умови. Після підстановки числових значень
Для знаходження оригіналу функції (primitive function) Uc(s) використовується формула розкладання. Тоді
y(s)=4,75×10-3s2 + 1,63s + 290; H(s)=s(2,3×10-3s2 + 4×10-3s + 1,16). Порівнюючи знаменник до нуля, знаходимо його корені: S1 = 0; S2 = - 80 + j200; S3 = - 80 – j200. Оскільки ми отримали три корені, то сума в формулі розкладу містить три складових (n=3):
Знайдемо числові значення чисельників:
y(s1)=4,75×10-3s12 + 1,63s1 + 290 = 290, y(s2)=4,75×10-3s22 + 1,63s2 + 290 = j174, y(s3)=4,75×10-3s32 + 1,63s3 + 290 = - j174. Похідна знаменника
H¢(s)=(2,5×10-3s2 + 4×10-3s + 1,16) + s(5×10-3s + 4×10-3), тому H¢(s1) = 1,16, H¢(s2) = - 2 – j0,8, H¢(s3) = - 2+ j0,8. Підставляючи отримані значення у вираз для uc(t), маємо:
або Замінимо показникові функції від уявного аргументу тригонометричними, тоді
uc(t)=250+81e-80t[cos(200t-111°50¢)+jsin(200t-111°50¢)+cos(200t-111°50¢)- -jsin(200t-111°50¢)]=250+162e-80tcos(200t-111°50¢), або
Інші шукані величини визначаються аналогічно.
|
|||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 494; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.203.158 (0.009 с.) |

 (1)
(1)
 . (2)
. (2) . (3)
. (3)
 .
.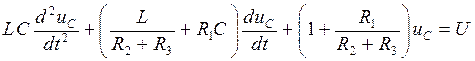 . (4)
. (4)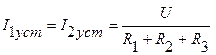 ,
,
 .
.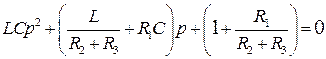

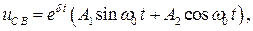
 ;
;
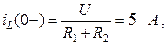


 маємо
маємо ,
, .
.











