
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Максвелла (теорема о взаимности единичных перемещений)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема Максвелла - это теорема о взаимности работ для частного случая нагружения системы, когда F1=F2=1. Очевидно, что при этом δ12=δ21. Перемещение точки первого состояния под действием единичной силы второго состояния равняется перемещению точки второго состояния под действием единичной силы первого состояния.
38. Формула для определения работы внутренних сил (с пояснением всех входящих в формулу величин). Теперь определим возможную работу внутренних сил. Для этого рассмотрим два состояния системы: 1) действует сила Pi и вызывает внутренние усилия Mi, Qi, Ni; 2) действует сила Pj, которая в пределах малого элемента dx вызывает возможные деформации DMj= Внутренние усилия первого состояния на деформациях (возможных перемещениях) второго состояния совершат возможную работу –dWij=MiDMj+QiDQj+NiDNj= Если проинтегрировать это выражение по длине элемента l и учесть наличие в системе n стержней, получим формулу возможной работы внутренних сил: –Wij= EI – жесткость при изгибе GA – Жесткость при сдвиге Е – модуль упругости характер физ параметры Е – модуль упругости характер геометрич параметры G- модуль сдвига A- площадь сечения EA –продольная жесткость
39. Формула Мора для определения перемещений (с пояснением всех входящих в формулу величин). Рассмотрим два состояния стержневой системы: 1) грузовое состояние (рис. 6.6 а), в котором действующая нагрузка вызывает внутренние усилия MP, QP, NP; 2) единичное состояние (рис. 6.6 б), в котором действующая единичная сила P=1 вызывает внутренние усилия
Рис. 6.6 Внутренние силы грузового состояния на деформациях единичного состояния –Vij= А единичная сила P=1 единичного состояния на перемещении грузового состояния DP совершает возможную работу Wij=1×DP=DP. По известному из теоретической механики принципу возможных перемещений в упругих системах эти работы должны быть равными, т.е. Wij= –Vij. Значит, должны быть равны и правые части этих выражений: DP= Эта формула называется формулой Мора и используется для определения перемещений стержневой системы от внешней нагрузки.
40. Порядок определения перемещений в С.О.С. с использованием формулы Мора. Определить выражения для внутренних усилий Np, Qp, Mp как функции координаты х произвольного сечения для всех участков стержневой системы от действия заданной нагрузки. Приложить по направлению искомого перемещения соответствующую ему единичную нагрузку (единичную силу, если определяется линейное перемещение; сосредоточенный единичный момент, если определяется угловое перемещение). Определить выражения для внутренних усилий Найденные выражения внутренних усилий в первом и втором состоянии подставляют в интеграл Мора и интегрируют по участкам в пределах всей стержневой системы. 41. Применение формулы Мора для определения перемещений в изгибаемых системах (со всеми пояснениями). В балках (рис. 6.7 а) возможны три случая: − если DP= − если 5≤ DP= 2. В рамах (рис. 6.7 б) элементы в основном работают только на изгиб.Поэтому в формуле Мора учитываются только моменты. В высоких рамах учитывается и продольная сила: DP= 3. В арках (рис. 6.7 в) необходимо учитывать соотношение между основными размерами арки l и f: 1) если 2) если 4. В фермах (рис. 6.7 г) возникают только продольные силы. Поэтому DP = 42. Правило Верещагина для вычисления интегралов Мора: суть и условия использования. Правило Верещагина для вычисления интегралов Мора: суть и условия использования.
c- центр тяжести площади грузовой эпюры. yc-ордината взята из единичной эпюры, расположенной под центром тяжести площади грузовой эпюры. EI- жесткость при изгибе.
Для вычисления полного перемещения необходимо сложить произведения грузовой эпюры на ординату поединично всех простых участков системы. В данной формуле приведены определенные перемещения от действий только изгибающего момента. Это справедливо для изгибающих систем, для которых основное влияние на перемещение точек оказывает величина изгибающего момента, а влияние поперечной и продольных сил незначительно,которыми на практике пренебрегают.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 867; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.006 с.) |


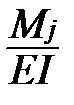 dx, DQj=m
dx, DQj=m  dx, DNj=
dx, DNj=  dx.
dx. dx+m
dx+m 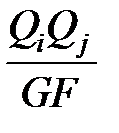 dx+
dx+  dx.
dx. dx.
dx. .
.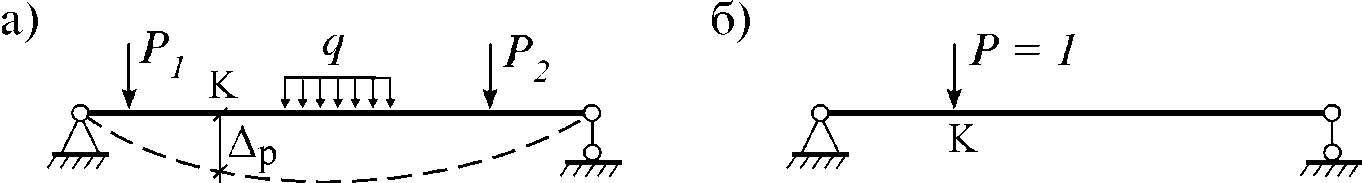
 ,
, 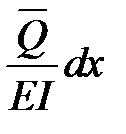 ,
,  совершают возможную работу
совершают возможную работу dx.
dx. dx.
dx. как функции координаты х произвольного сечения для всех участков стержневой системы от действия единичной нагрузки.
как функции координаты х произвольного сечения для всех участков стержневой системы от действия единичной нагрузки. > 8, в формуле оставляется только член с моментами:
> 8, в формуле оставляется только член с моментами: ;
;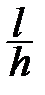 ≤8, учитываются и поперечные силы:
≤8, учитываются и поперечные силы: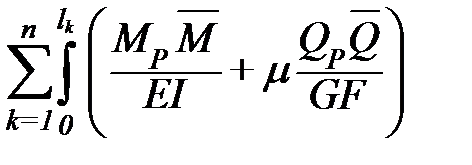 dx;
dx; dx.
dx. £ 5 (крутая арка), учитываются только моменты;
£ 5 (крутая арка), учитываются только моменты;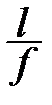 >5 (пологая арка), учитываются моменты и продольные силы.
>5 (пологая арка), учитываются моменты и продольные силы. dx =
dx = 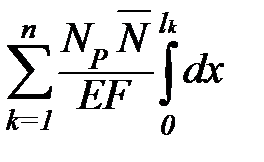 =
=  .
.





