Классификация сооружений по особенностям работы.

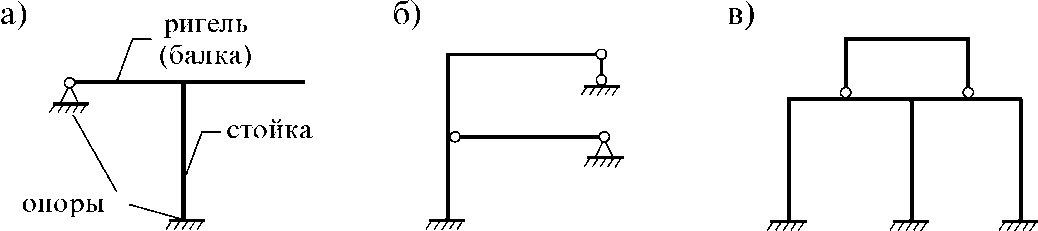
Ну не знаю, если картинки не нужны - удаляйте

По особенностям работ:

Балки, рамы, арки, фермы, вантовые системы, комбинированные, массивные, кессонные, фундаменты

1. Балка – изгибаемый брус. Она бывает однопролетной или много-пролетной. Типы однопролетных балок: простая балка (рис. 1.5 а), консоль (рис. 1.5 б) и консольная балка (рис. 1.5 в). Многопролетные балки бывают разрезные (рис. 1.5 г), неразрезные (рис. 1.5 д) и составные (рис. 1.5 е):

Рис. 1.5

2. Рама – система прямых (ломаных или кривых) стержней. Ее стержни могут соединяться жестко или через шарнир. Вот некоторые типы рам: простая рама (рис. 1.6 а), составная рама (рис. 1.6 б), многоэтажная рама (рис. 1.6 в).

Рис. 1.6

3. Ферма – система стержней, соединенных шарнирами. Типов ферм много. Например, бывают стропильная ферма (рис. 1.7 а), мостовая ферма (рис. 1.7 б), крановая ферма (рис. 1.7 в), башенная ферма (рис. 1.7 г).

Рис. 1.7

4. Арка – система из кривых стержней. Некоторые типы арок: трехшарнирная (рис. 1.8 а), одношарнирная (рис. 1.8 б), бесшарнирная (рис. 1.7 в) арки.

Рис. 1.8

Существуют более сложные системы как комбинации простых систем. Они называются комбинированными системами. Например: арочная ферма (рис. 1.9 а), ферма с аркой (рис. 1.9 б), висячая система (рис. 1.9 в):

Рис. 1.9

По статическим особенностям различают статически определимые и статически неопределимые системы.

 

Основные гипотезы и принципы, положенные в основу классических методов расчета строительной механики.

Большинство материалов сооружений при действии малых нагрузок являются упругими и подчиняются закону Гука. При возрастании нагрузки этот закон перестает выполняться. будем рассматривать только упругие материалы.

Примем некоторые гипотезы, которые позволяют выбирать более простые расчетные модели, упрощать и уменьшать объем вычислений:

1. Материал сооружения является упругим.

2. Перемещения точек сооружения намного меньше его размеров.

3. Перемещения пропорциональны величине нагрузки.

4. Выполняется принцип суперпозиции (независимости действия сил): результат воздействия нескольких сил равен сумме воздействий отдельных сил и не зависит от порядка приложения этих сил.

Объектом исследования в строительной механике является идеально упругое тело, наделенное следующими свойствами:

– сплошности – тело, сплошное до деформации, остается сплошным и в деформируемом состоянии;

– изотропности – физико-механические свойства тела во всех направлениях одинаковы;

– однородности – свойства тела одинаковы во всех точках тела.

Принято считать, что при рассмотрении задач строительной механики, деформации малы по сравнению с единицей, а перемещения – по сравнению с размерами тела. Эта гипотеза позволяет рассматривать в нагруженном состоянии недеформированную форму тела (какую блин форму?). Кроме того, в основу положена линейная связь между внешними силами и перемещениями или между деформациями и напряжениями. Указанные гипотезы упро­щают решение задач строительной механики, не искажая при этом действительную картину напряженно-деформированного состояния тела. В силу введенных гипотез уравнения, описывающие это состояние, являются линейными, что позволяет, в свою очередь, применить принцип независимости действия сил (суперпозиции)

5. Внутренние усилия в плоских стержневых системах (определение). Способы и по­рядок их определения. Метод сечений и его применение.

Под действием внешних нагрузок в каждом конструктивном элементе сооружения возникают внутренние усилия, которые, сопротивляясь внешним воздействиям, препятствуют разрушению конструктивных элементов и зависят от физических свойств материалов, из которых изготовлены элементы. Внутренние усилия – это количественная мера взаимодействия двух частей одного тела, расположенных по разные стороны сечения и вызванные действием внешних усилий. Внутренние усилия возникают непосредственно в деформируемом теле.

Условно задачу определения внутренних усилий можно разбить на два этапа:

1. Определение реакций опор, при помощи которых сооружение связано с основанием и реакций связей отдельных жестких дисковдруг с другом.

2. Определение внутренних усилий и построение их эпюр.

Метод сечений

Внутренние усилия в любом конструктивном элементе определяются методом сечения. Чуть которого заключается в том, чтобы рассечь систему на 2 части и, отбросив одну, рассм. равновесие отсеченной части, определить внутренние усилия, составл. уравнения моментов или проекций сил.

Способ вырезания узлов.

Суто его заключается в последовательном вырезании тех узлов фермы, где соединяются не более 2 стержней с неизвестными усилиями. Это вытекает из положения, что узел является точкой, а точка на плоскости имеет лишь 2 степени свободы, поэтому для узла можно составить лишь 2 уравнения проекций сил на соответствующие оси, при этом эти уравнения составляют атким образом, чтобы уравнение включало лишь 1 неизвестное усилие. Достоинство способа в его простоте, а недостатки в том, что невозможно сразу определить усилия в середине фермы, и то, что погрешности при определении усилий в стержнях накапливаются.

Правило о нулевых стержнях:1) Если в неразгруженном узле собираются 2 стержня, то усилия в них равны 0. 2)Если в неразгруженном узле соедин. 3 стержня, 2 из которых находятся на 1 прямой, то усилия в них равны, а в 3 – равны 0. 3) Если в загруженном узле соединяются 2 стержня, 1 из которых лежит на 1 прямой с лишней нагрузкой, то усилия в этом стержне = внешней нагрузке, а во 2 = 0.

Способ моментной точки:

Суть способа заключается в том, чтобы провести сечение таким способом, когда усилия во всех стержнях попадают в сечение, кроме одного, усилие в котором можно определить пересечением в 1 точке. Для определения этого усилия составляется уравнение моментов для отсеченной левой или правой части фермы, относительно точки, в которой пересекаются стержни, эту точку принимают моментной.

Способ проекций:

Суть его заключается в том, чтобы последовательно провести сечение таким способом

Когда все стержни, кроме проецируемого, усилие в кот. необходимо определить, параллельны. Для определения усилий в этом стержне след. составить уравнение на ось перпендикулярную параллельным стержням.