Расчетная схема сооружения, проблемы ее выбора.

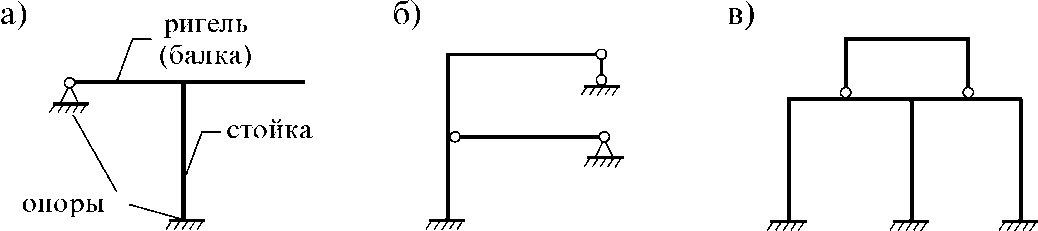
Расчетная схема сооружения, проблемы ее выбора.

Расчётная схема сооружения — Упрощённая идеализированная схема, которая наиболее точно учитывает основные особенности распределения внутренних усилий по длине элементов системы от действия внешних нагрузок и пренебрегает второстепенными особенностями. Различают несколько видов расчётных схем, отличающихся основными гипотезами, положенными в основу расчёта, а также используемым при расчёте математическим аппаратом.

Классификация расчётных схем

По характеру учёта пространственной работы – одно-, двух- и трёхмерные.

• По виду неизвестных – дискретные, дискретно-континуальные и континуальные.

• По виду конструкций, положенных в основу расчётной схемы – стержневые, пластинчатые, оболочковые и массивные.

• По учёту инерционных сил – статические и динамические.

Расчётная схема состоит из условных элементов: стержней, пластин, оболочек, массивов и связей.

Стержни используют в расчётных схемах стержневых конструкций (стоек, балок, арок и др.), систем из таких конструкций (ферм, рам, сетчатых оболочек), а также для приближённого расчёта плоскостных конструкций (например, несущих стен зданий).

Оболочки являются расчётной схемой различных пространственных конструкций (куполов, сводов, оболочек).

Элементы соединяются жёстко либо шарнирно и опираются на основание при помощи опор (кто бы мог подумать???)

Связи в расчётных схемах соединяют между собой отдельные элементы, а также конструкцию с основанием. В расчётных схемах связи различаются по числу степеней свободы, которые они отнимают от системы.

Выбор расчетной схемы начинается со схематизации свойств материала и характера деформирования твердого тела, затем выполняется схематизация геометрической формы реального объекта. Выбор расчетной схемы является сложной и ответственной частью расчета. От него в первую очередь зависит качество расчета. Расчет по неправильно выбранной расчетной схеме не может быть достоверным даже при использовании самых точных методов. в зависимости от поставленной задачи расчетная схема может видоизменяться. Отказываясь от того или иного упрощения или заменяя его менее грубым, можно получить более точную расчетную схему.

 

Виды опор и их свойства

Жёсткая заделка0 степеней свободы,3 связи, возникают реакции R M H

Шарнирно-неподвижная 1 степень свободы, 2 связи, возникают реакции R H

Шарнирно-подвижная 2 степени свободы 1 связи, возникают реакции R M H

Плавающая заделка1 степеней свободы 2 связи, возникают реакции R M

 

 

Классификация сооружений по особенностям работы.

Ну не знаю, если картинки не нужны - удаляйте

По особенностям работ:

Балки, рамы, арки, фермы, вантовые системы, комбинированные, массивные, кессонные, фундаменты

1. Балка – изгибаемый брус. Она бывает однопролетной или много-пролетной. Типы однопролетных балок: простая балка (рис. 1.5 а), консоль (рис. 1.5 б) и консольная балка (рис. 1.5 в). Многопролетные балки бывают разрезные (рис. 1.5 г), неразрезные (рис. 1.5 д) и составные (рис. 1.5 е):

Рис. 1.5

2. Рама – система прямых (ломаных или кривых) стержней. Ее стержни могут соединяться жестко или через шарнир. Вот некоторые типы рам: простая рама (рис. 1.6 а), составная рама (рис. 1.6 б), многоэтажная рама (рис. 1.6 в).

Рис. 1.6

3. Ферма – система стержней, соединенных шарнирами. Типов ферм много. Например, бывают стропильная ферма (рис. 1.7 а), мостовая ферма (рис. 1.7 б), крановая ферма (рис. 1.7 в), башенная ферма (рис. 1.7 г).

Рис. 1.7

4. Арка – система из кривых стержней. Некоторые типы арок: трехшарнирная (рис. 1.8 а), одношарнирная (рис. 1.8 б), бесшарнирная (рис. 1.7 в) арки.

Рис. 1.8

Существуют более сложные системы как комбинации простых систем. Они называются комбинированными системами. Например: арочная ферма (рис. 1.9 а), ферма с аркой (рис. 1.9 б), висячая система (рис. 1.9 в):

Рис. 1.9

По статическим особенностям различают статически определимые и статически неопределимые системы.

 

Метод сечений

Внутренние усилия в любом конструктивном элементе определяются методом сечения. Чуть которого заключается в том, чтобы рассечь систему на 2 части и, отбросив одну, рассм. равновесие отсеченной части, определить внутренние усилия, составл. уравнения моментов или проекций сил.

Способ вырезания узлов.

Суто его заключается в последовательном вырезании тех узлов фермы, где соединяются не более 2 стержней с неизвестными усилиями. Это вытекает из положения, что узел является точкой, а точка на плоскости имеет лишь 2 степени свободы, поэтому для узла можно составить лишь 2 уравнения проекций сил на соответствующие оси, при этом эти уравнения составляют атким образом, чтобы уравнение включало лишь 1 неизвестное усилие. Достоинство способа в его простоте, а недостатки в том, что невозможно сразу определить усилия в середине фермы, и то, что погрешности при определении усилий в стержнях накапливаются.

Правило о нулевых стержнях:1) Если в неразгруженном узле собираются 2 стержня, то усилия в них равны 0. 2)Если в неразгруженном узле соедин. 3 стержня, 2 из которых находятся на 1 прямой, то усилия в них равны, а в 3 – равны 0. 3) Если в загруженном узле соединяются 2 стержня, 1 из которых лежит на 1 прямой с лишней нагрузкой, то усилия в этом стержне = внешней нагрузке, а во 2 = 0.

Способ моментной точки:

Суть способа заключается в том, чтобы провести сечение таким способом, когда усилия во всех стержнях попадают в сечение, кроме одного, усилие в котором можно определить пересечением в 1 точке. Для определения этого усилия составляется уравнение моментов для отсеченной левой или правой части фермы, относительно точки, в которой пересекаются стержни, эту точку принимают моментной.

Способ проекций:

Суть его заключается в том, чтобы последовательно провести сечение таким способом

Когда все стержни, кроме проецируемого, усилие в кот. необходимо определить, параллельны. Для определения усилий в этом стержне след. составить уравнение на ось перпендикулярную параллельным стержням.

Расчет составных рам.

проводим Кинематический анализ

далее определяем опорные реакции

строи поэтажную схему

построение эпюры изгибающих моментов

5) построение линий влияний

6)определение усилий линий влияния

25. Определение внутренних сил в трехшарнирных арках от действия внешней статической нагрузки (сравнение с балками того же пролета).

Расчет арки обычно ведется следующим образом:

– арка мысленно разбивается на ряд участков, чтобы в сечения обязательно попали сосредоточенные силы и дополнительные, так как эпюры внутренних сил впри любой нагрузке криволинейны. Следует предусмотреть достаточное количество сечений для достижения точности расчета;

Определение опорных реакций в таких системах ничем не отличается от соответствующих расчетов в трех шарнирных рамах. Внутренние усилия М, Q, N тоже могут быть определены на основе общих подходов, рассмотренных для рам. Интерес здесь представляет получение выражений для усилий в арке через соответствующие выражения для простой балки, с таким же пролетом, как и у арки.

Теорема Клапейрона.

Теорема Клапейрона.

теорема Клапейрона: упругая работа внешней силы при статическом приложении равна половине произведения ее окончательного значения на соответствующее этой силе перемещение.

А₁₁=1/2*Р₁*∆₁₂ –действительная работа

А₁₂=Р₁*∆₁₂-возможная работа

35. Возможная работа внешних и внутренних сил с пояснениями всех входящих в формулы величин (понятия и формулы для расчета).

35. Возможная работа внешних и внутренних сил с пояснениями всех входящих в формулы величин (понятия и формулы для расчета).

Рассмотрим 2 состояния системы:

В первом состоянии система загружена i-ая

 

 

Возможная работа i-ого состояния при действии на перемещение точек их приложения вызван вызван действием сил К-ого может быть определена при рассмотрении определенно продольных, поперечных сил, изгиб, моментов аналогично как и работа действительная

 

Расчетная схема сооружения, проблемы ее выбора.

Расчётная схема сооружения — Упрощённая идеализированная схема, которая наиболее точно учитывает основные особенности распределения внутренних усилий по длине элементов системы от действия внешних нагрузок и пренебрегает второстепенными особенностями. Различают несколько видов расчётных схем, отличающихся основными гипотезами, положенными в основу расчёта, а также используемым при расчёте математическим аппаратом.

Классификация расчётных схем

По характеру учёта пространственной работы – одно-, двух- и трёхмерные.

• По виду неизвестных – дискретные, дискретно-континуальные и континуальные.

• По виду конструкций, положенных в основу расчётной схемы – стержневые, пластинчатые, оболочковые и массивные.

• По учёту инерционных сил – статические и динамические.

Расчётная схема состоит из условных элементов: стержней, пластин, оболочек, массивов и связей.

Стержни используют в расчётных схемах стержневых конструкций (стоек, балок, арок и др.), систем из таких конструкций (ферм, рам, сетчатых оболочек), а также для приближённого расчёта плоскостных конструкций (например, несущих стен зданий).

Оболочки являются расчётной схемой различных пространственных конструкций (куполов, сводов, оболочек).

Элементы соединяются жёстко либо шарнирно и опираются на основание при помощи опор (кто бы мог подумать???)

Связи в расчётных схемах соединяют между собой отдельные элементы, а также конструкцию с основанием. В расчётных схемах связи различаются по числу степеней свободы, которые они отнимают от системы.

Выбор расчетной схемы начинается со схематизации свойств материала и характера деформирования твердого тела, затем выполняется схематизация геометрической формы реального объекта. Выбор расчетной схемы является сложной и ответственной частью расчета. От него в первую очередь зависит качество расчета. Расчет по неправильно выбранной расчетной схеме не может быть достоверным даже при использовании самых точных методов. в зависимости от поставленной задачи расчетная схема может видоизменяться. Отказываясь от того или иного упрощения или заменяя его менее грубым, можно получить более точную расчетную схему.

 

Виды опор и их свойства

Жёсткая заделка0 степеней свободы,3 связи, возникают реакции R M H

Шарнирно-неподвижная 1 степень свободы, 2 связи, возникают реакции R H

Шарнирно-подвижная 2 степени свободы 1 связи, возникают реакции R M H

Плавающая заделка1 степеней свободы 2 связи, возникают реакции R M