
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическое описание процессовСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Глава вторая МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ПРОЦЕССОВ В АСИНХРОННОМ ДВИГАТЕЛЕ
Положительные направления Электромагнитных величин При математическом описании процессов в асинхронном двигателе все переменные рассматриваются в виде комплексов или в виде векторов. Для каждой из переменных назначаются определённые положительные направления. В разных странах и разные авторы из отдельных стран пользуются разными возможными сочетаниями положительных направлений для токов, ЭДС и напряжений в электрических цепях переменного тока [8]. В зависимости от того, как выбраны эти положительные направления, меняется математическое описание и вид векторных диаграмм. В технической литературе находят применение два подхода по назначению положительных направлений для ЭДС и напряжений. Один из них сводится к следующему. Назначается положительное направление тока между источником питания и приёмником. За положительное направление ЭДС, наводимой в катушке, принимается направление, совпадающее с направлением тока, вне зависимости от того, какова физическая природа возникновения ЭДС. Наведённая в катушке ЭДС может представлять собой ЭДС самоиндукции, взаимоиндукции или ЭДС вращения. Положительное направление для напряжений принимается с учётом направления потока электрической энергии. При втором подходе положительные направления для ЭДС и напряжений назначаются исходя из наглядности физических представлений, но в этом случае вероятность возникновения ошибок при выполнении расчётов возрастает. При математическом описании процессов, особое внимание следует уделять знакам для переменных, а при построении векторных диаграмм важно не ошибиться в расстановке направлений стрелок для переменных.
Схемы замещения асинхронного двигателя при Постоянной частоте
Различают физическую и расчётную схему замещения. Физическая схема (рис.2.1) содержит два контура: один из них для статора, а второй для ротора.
Эта схема наглядно отражает явления, протекающие в одной из фаз статора и ротора. Однако при выполнении расчётов возникают определённые трудности, связанные с тем, что статор неподвижен, а ротор вращается со скоростью
Обратим внимание на расположение стрелок. Стрелки направлены в положительном направлении. Положительные направления назначены в соответствии с ранее отмеченным первым способом. В двигательном режиме ток статора протекает от источника питания. Вращающийся магнитный поток
Ток протекает от положительного потенциала (точка 1) к отрицательному потенциалу (точка 3). Положительные направления для напряжений При втором подходе к назначению положительных направлений для переменных поступают следующим образом. Назначают, как и ранее, положительное направление тока статора. Положительное направление для ЭДС
Рассмотренный приём обычно используют в электрических машинах постоянного тока, для которых в (2.2) отсутствует знак минус перед переменной Если в (2.2) разделить обе части второго уравнения на s, то процессы будут описываться уравнениями:
В этом случае ротор представляется неподвижным. ЭДС ротора и индуктивное сопротивление рассеяния ротора уже не зависят от скольжения. Вращение машины учитывается фиктивным сопротивлением ротора Далее, с целью упрощения расчётов, переменные и параметры ротора приводят к числу витков статора, то есть принимают
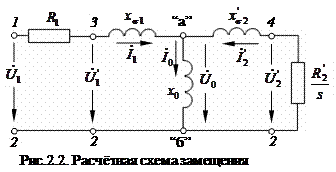
где - Для приведенных величин направление стрелок на рис.2.1 и математическое описание процессов (2.3) остаются прежними. Добавляется лишь символ штрих для переменных и параметров ротора. Так как после приведения Таким образом, с целью упрощения расчётов, выполнен переход от физической схемы замещения (рис.2.1) к расчётной схеме замещения (рис.2.2).
В этой схеме возникает электрическая связь между статором и ротором, а между точками “а” и “б” возникает цепь для протекания тока намагничивания В отличие от двигателей постоянного тока, в которых магнитный поток создается постоянным током с помощью специальной обмотки возбуждения, у асинхронных двигателей такой обмотки нет. Обмотка статора одновременно является как рабочей обмоткой, так и обмоткой возбуждения, а магнитное поле создается переменным током возбуждения
Наведенная в статоре ЭДС пропорциональна скорости изменения потокосцепления в воздушном зазоре
Последовательно переходя к току возбуждения, получим:
Напряжение для цепи намагничивания
Эти уравнения записаны для мгновенных значений переменных. Переходя к векторной форме записи, получим:
Из этих уравнений следует, что ЭДС Результирующий магнитный поток
Связь между током намагничивания и магнитным потоком характеризуется кривой намагничивания
Расчёт действующих значений ЭДС, наводимых в статоре и роторе, выполняется по (1.31), (1.33) или по формуле
По правилам общей электротехники напряжения на отдельных участках схемы замещения (рис.2.2) можно выразить через потокосцепления:
Здесь введены обозначения:
Эти понятия являются очень важными, они будут использоваться дальше и заслуживают особого внимания:
Найдём связь между токами
Здесь:
Решая (2.15) относительно токов
Отсюда можно перейти к амплитудным, а затем к действующим значениям:
Выбор той или иной схемы замещения определяется конкретно поставленной задачей и простотой приемов по достижению конечной цели. С помощью схемы на рис.2.1 проще представлять физические явления. Схема же на рис.2.2 близка к схеме замещения трансформатора и позволяет сравнительно просто устанавливать связи между переменными, выполнять расчёты, строить векторные диаграммы, и проводить анализ протекающих процессов. Связь между отдельными переменными в наглядном виде представляется с помощью векторной диаграммы (рис.2.3). Рассмотрение этой диаграммы проведём в порядке её построения. Изображается комплексная плоскость с действительной осью “+” и мнимой осью “j”. Вдоль действительной оси направим вектор тока Так как переменные ротора приведены к числу витков статора, то такая же ЭДС наводится и в роторе
Напомним, что ротор представлен неподвижным, а его вращение учитывается фиктивным сопротивлением
Вектор напряжения
Под действием ЭДС ротора протекает ток ротора
Ток Косинус этого угла
Обратите внимание, что угол Проекция вектора тока
Эта составляющая тока ротора создаёт электромагнитный момент. По известным векторам Вектор полного потокосцепления ротора с учётом полей рассеяния располагается на векторной диаграмме в соответствии с равенством
Здесь потокосцепление рассеяния ротора Потокосцепление ротора
Отсюда следует, что вектор напряжения Напряжение
На диаграмме (рис.2.3) вектора Вектор полного потокосцепления статора
Потокосцепление
Этот вектор опережает вектор Построение векторной диаграммы завершается изображением вектора напряжения
или
где В последнем уравнении напряжение
Из (2.24) и из схемы замещения (рис.2.2) следует, что если не учитывать падение напряжения в статоре
Покажем, как можно учесть влияние падения напряжения в статоре на величину потокосцепления Уравнение (2.24) с учётом (2.15) и (2.16) приводится к виду
Решая его относительно
Выполнив соответствующие действия с комплексными величинами, и осуществив переход к действующим значениям, получим [6]
где Связь между
Зависимости
При идеальном холостом ходе
В области генераторного режима (s<0) Выводы: 1. Напряжения на отдельных участках схемы замещения пропорциональны соответствующим потокосцеплениям и синхронной скорости поля
2. При идеальном холостом ходе магнитный поток через воздушный зазор пропорционален приложенному напряжению и обратнопропорционален частоте 3. При изображении схем замещения и векторных диаграмм особое внимание следует уделять расстановке направлений стрелок для переменных.
При частотном регулировании
При частотном регулировании частоту переменных статора и синхронную скорость поля обычно представляют в относительных единицах
где От скольжения s переходят к абсолютному скольжению
Здесь за базовую величину принята синхронная скорость поля при номинальной частоте. Связь между
Ротор, как и ранее, представляется заторможенным, а его параметры приведены к числу витков статора. Все индуктивные сопротивления и напряжения на отдельных участках схемы замещения зависят от частоты:
Уравнения для напряжений (2.13) принимают вид:
В этих уравнениях индуктивные сопротивления
Эти равенства очень важные, так как характеризуют основные законы частотного регулирования:
При частотном регулировании скорости вниз от номинальной скорости ( Регулирование скорости вверх от номинальной скорости выполняют при ослабленном поле. В этом случае напряжение поддерживают на постоянном уровне. Выражения для ЭДС статора и ротора можно представлять в разных формах записи:
Связь между токами устанавливается по ранее рассмотренной методике. Из схемы замещения видно, что при Выводы: 1. Магнитный поток 2. При частотном регулировании приходится регулировать не только частоту, но и модуль напряжения.
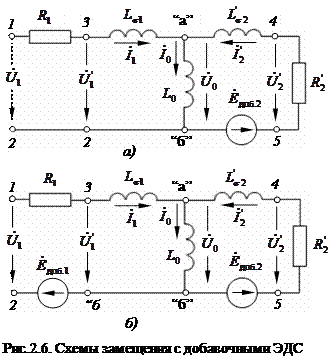
С добавочными ЭДС
В электроприводах переменного тока вопросы динамики обычно решаются с помощью теории обобщённой электрической машины. В работах [9,10] отмечается, что с помощью схем замещения можно решать не только задачи статики, но и динамики. Покажем, что между схемой замещения АД и теорией обобщённой электрической машины имеется тесная связь. На рис.2.6 изображены две схемы замещения АД. Первая схема (а) относится к процессам в неподвижных системах координат:
В приведенных схемах предполагается, что переменные и параметры ротора приведены к числу витков статора. Обмотки статора и ротора находятся в магнитном поле, вращающемся со скоростью
Положительные направления для этих ЭДС приняты совпадающими с направлением токов. В частном случае, когда система координат неподвижна, дополнительная ЭДС вводится только в ротор
Вначале рассмотрим математическое описание процессов при неподвижной системе координат (рис.2.6а). В контуре тока статора последовательно соединены две индуктивности Проходя последовательно вдоль контуров, получаем уравнения для напряжений в контурах статора и ротора:
Если для контура ротора напряжение
Первый и последний члены этого уравнения в сумме характеризуют ЭДС самоиндукции, наводимую в роторе потокосцеплением
С учётом (2. 38) уравнение для контура ротора может быть записано в одной из следующих форм записи:
Таким образом, электромагнитные процессы в одной фазе описываются системой уравнений:
В этой системе уравнений скорость
Взаимную ориентацию переменных во временной области удобно рассматривать с помощью векторной диаграммы на рис.2.7. В этой диаграмме учитывается добавочная ЭДС в роторе и выполнены дополнительные построения в предположении, что  < <  . .
Раскроем физическую сущность отдельных составляющих в системе уравнений (2.40). Выражение Выражение Выражение Из рис.2.6 и уравнения (2.40) следует, что при неподвижном роторе Перейдём к схеме замещения на рис.2.6б. Проходя, как и раньше, последовательно по контурам, получим:
Выражая
В правой части этих уравнений присутствуют ЭДС двух видов с разной физической сущностью:
Векторная диаграмма на рис.2.7 отражает процессы в одной фазе. Для создания электромагнитного момента обязательно нужна ещё одна или две фазы. В этом случае состояния переменных рассматривают с помощью пространственных векторных диаграмм. Направим вдоль действительной оси + геометрическую ось фазы “а”, а вдоль мнимой оси расположим геометрическую ось фазы “b”. Получили пространственную плоскость поперечного сечения машины. На этой плоскости уже изображены в виде векторов все переменные. Известно, что в ортогональных системах координат модули временных и пространственных векторов одинаковы. В этом случае временные и пространственные векторные диаграммы принимают одинаковый вид, изменяется лишь символика для переменных. Изменив символику, то есть, заменив точку над переменной чертой над переменной, получим пространственную векторную диаграмму. Если теперь сравнивать процессы во временной и пространственной областях, то они совершенно разные. В пространственной области изображающие вектора вращаются относительно геометрических осей отдельных фаз и отражают процессы во всех фазах. Во временной области вектора вращаются относительно комплексной плоскости и отражают процессы только в одной фазе. Если их поведение рассматривать относительно геометрической оси рассматриваемой фазы, то они пульсируют во времени. Вернёмся к уравнениям (2.41), которые описывают процессы во временной области, Если в этих уравнениях изменить всего лишь символику для переменных, то получим математическое описание процессов в пространственной области:
Эти уравнения являются основополагающими в теории обобщённой электрической машины, так как описывают электромагнитные процессы в статике и динамике. Таким образом, путём простых преобразований, установлена связь между схемой замещения и теорией обобщённой электрической машины. Эта связь стала возможной благодаря введению в схему замещения добавочных ЭДС, которые описываются уравнениями (2.38) и (2.39).
2.5. Процесс преобразования энергии и Электромагнитный момент Асинхронный двигатель потребляет от источника питания активную и реактивную мощность. Активную мощность можно записать в виде скалярного произведения вектора напряжения на вектор тока
Напомним, что здесь Реактивная мощность идёт на создание главного поля и полей рассеяния
Важным энергетическим показателем является коэффициент мощности
Активная мощность состоит из двух составляющих
Первая составляющая представляет собой мощность потерь в активных сопротивлениях статора
Разность между мощностью
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 726; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.188.75 (0.017 с.) |


 . Это приводит к тому, что переменные в статоре и роторе меняются с разными частотами. Угловая частота переменных в статоре
. Это приводит к тому, что переменные в статоре и роторе меняются с разными частотами. Угловая частота переменных в статоре 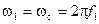 , а в роторе
, а в роторе  . ЭДС ротора и индуктивное сопротивление рассеяния ротора пропорциональны скольжению:
. ЭДС ротора и индуктивное сопротивление рассеяния ротора пропорциональны скольжению: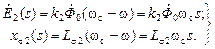 (2.1)
(2.1) наводит в статоре и роторе ЭДС вращения
наводит в статоре и роторе ЭДС вращения  ,
,  . Эти ЭДС наводятся результирующим магнитным потоком
. Эти ЭДС наводятся результирующим магнитным потоком 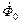 , они совпадают с направлением токов и направлены в одну сторону. Фактические направления для остальных переменных определяются режимом работы. В двигательном режиме фактическое направление
, они совпадают с направлением токов и направлены в одну сторону. Фактические направления для остальных переменных определяются режимом работы. В двигательном режиме фактическое направление  действует встречно току
действует встречно току 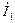 . Это учитывают следующим приёмом. Положительное направление стрелки для ЭДС
. Это учитывают следующим приёмом. Положительное направление стрелки для ЭДС 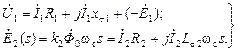 (2.2)
(2.2) направлены встречно положительному направлению ЭДС
направлены встречно положительному направлению ЭДС 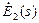 и ток ротора
и ток ротора 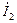 направлены согласно, то есть ЭДС ротора является источником электрической энергии для контура ротора
направлены согласно, то есть ЭДС ротора является источником электрической энергии для контура ротора можно сохранить прежнее или изменить на обратное направление. В первом случае
можно сохранить прежнее или изменить на обратное направление. В первом случае 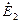 совпадало с направлением
совпадало с направлением  (2.3)
(2.3) . Частота переменных в статоре и роторе становится одинаковой
. Частота переменных в статоре и роторе становится одинаковой  .
.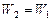 . Приведенные величины отмечают штрихом:
. Приведенные величины отмечают штрихом: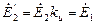 ;
; 
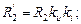
 , а коэффициенты приведения для напряжения и тока рассчитывают по формулам:
, а коэффициенты приведения для напряжения и тока рассчитывают по формулам: (2.4)
(2.4) и
и 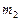 число фаз статора и ротора.
число фаз статора и ротора. и
и 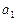 и
и 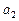 соединим. Соединим и точки
соединим. Соединим и точки 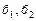 .
.
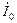 .
.
 (2.5)
(2.5) (2.6)
(2.6) (2.7)
(2.7) (2.8)
(2.8) (2.9)
(2.9) , отстаёт от тока
, отстаёт от тока 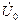 действует встречно ЭДС и опережает ток на 90 электрических градусов. С целью не загромождения рис.2.2 стрелка для ЭДС
действует встречно ЭДС и опережает ток на 90 электрических градусов. С целью не загромождения рис.2.2 стрелка для ЭДС  не приводится.
не приводится. (2.10)
(2.10) . Если насыщение не учитывается, то есть индуктивность цепи намагничивания
. Если насыщение не учитывается, то есть индуктивность цепи намагничивания 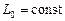 , то эта связь описывается равенством
, то эта связь описывается равенством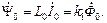 (2.11)
(2.11) (2.12)
(2.12)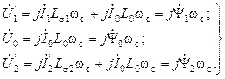 (2.13)
(2.13)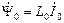 - главное потокосцепление или потокосцепление через воздушный зазор;
- главное потокосцепление или потокосцепление через воздушный зазор;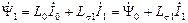 - полное потокосцепление статора с учётом полей рассеяния;
- полное потокосцепление статора с учётом полей рассеяния; - полное потокосцепление ротора с учётом полей рассеяния.
- полное потокосцепление ротора с учётом полей рассеяния.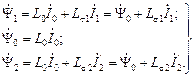 (2.14)
(2.14) (рис.2.2). Вначале выразим напряжение между точками “а” и “б” через токи
(рис.2.2). Вначале выразим напряжение между точками “а” и “б” через токи 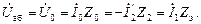 , (2.15)
, (2.15) - комплексное сопротивление контура намагничивания;
- комплексное сопротивление контура намагничивания;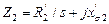 - комплексное сопротивление ротора;
- комплексное сопротивление ротора; - эквивалентное сопротивление при параллельном соединении сопротивлений
- эквивалентное сопротивление при параллельном соединении сопротивлений  и
и  .
. , находим:
, находим: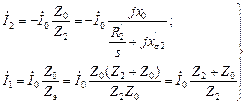 (2.16)
(2.16)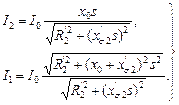 (2.17)
(2.17)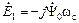 . Символ “
. Символ “  ” свидетельствует о том, что вектор
” свидетельствует о том, что вектор 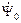 на 90 электрических градусов.
на 90 электрических градусов.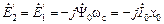 . (2.18)
. (2.18) .
.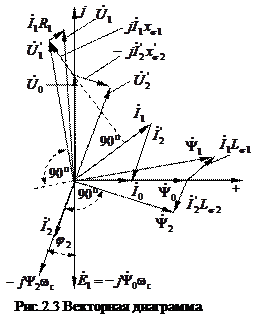
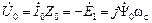 . (2.19)
. (2.19)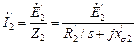 .
.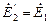 на угол
на угол 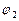 .
.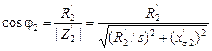 . (2.20)
. (2.20) зависит только от параметров ротора и от скольжения.
зависит только от параметров ротора и от скольжения. ” является активной составляющей тока ротора
” является активной составляющей тока ротора .
. . (2.21)
. (2.21) совпадает по направлению с вектором
совпадает по направлению с вектором  наводит в роторе ЭДС. Встречно этой ЭДС действует вектор напряжения
наводит в роторе ЭДС. Встречно этой ЭДС действует вектор напряжения . (2.22)
. (2.22)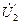 опережает вектор
опережает вектор 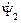 на 90 градусов и действует встречно с вектором тока
на 90 градусов и действует встречно с вектором тока  можно выразить и через напряжение
можно выразить и через напряжение  .
.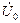 и
и 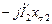 образуют треугольник.
образуют треугольник.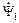 является результатом сложения векторов
является результатом сложения векторов 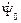 и
и 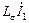
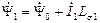 . (2.23)
. (2.23)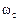 , наводит в статоре ЭДС, отстающую от вектора
, наводит в статоре ЭДС, отстающую от вектора 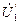
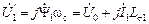 .
. часто называют напряжением за активным сопротивлением статора (рис.2.2). Символ “штрих” – это не символ приведения, он подразумевает учёт падания напряжения на активном сопротивлении статора.
часто называют напряжением за активным сопротивлением статора (рис.2.2). Символ “штрих” – это не символ приведения, он подразумевает учёт падания напряжения на активном сопротивлении статора.
 , (2.24)
, (2.24)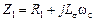 - комплексное сопротивление, учитывающее активное сопротивление и индуктивное сопротивление рассеяния статора.
- комплексное сопротивление, учитывающее активное сопротивление и индуктивное сопротивление рассеяния статора.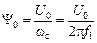 . (2.25)
. (2.25) , то уравнение (2.24) приводится к виду
, то уравнение (2.24) приводится к виду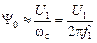 (2.26)
(2.26) .
.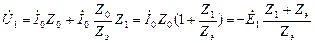 .
.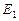 , имеем
, имеем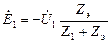 . (2.27)
. (2.27) , (2.28)
, (2.28)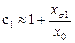 - коэффициент, характеризующий рассеяние статора. У асинхронных двигателей
- коэффициент, характеризующий рассеяние статора. У асинхронных двигателей  .
. . С учётом (2.28) получим
. С учётом (2.28) получим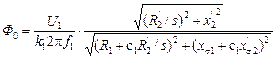 . (2.29)
. (2.29)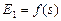 и
и  при
при 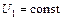 в качественном виде изображены на рис.2.4.
в качественном виде изображены на рис.2.4.
 =(0,98 ÷0,93)
=(0,98 ÷0,93)  ,
, 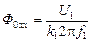 (2.30)
(2.30)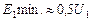 . Причина изменения
. Причина изменения 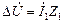 . Этот вывод следует из схем замещения. Аналогичное явление наблюдается и у двигателей постоянного тока. Отличительная особенность состоит в том, что у асинхронного двигателя все переменные являются комплексными величинами.
. Этот вывод следует из схем замещения. Аналогичное явление наблюдается и у двигателей постоянного тока. Отличительная особенность состоит в том, что у асинхронного двигателя все переменные являются комплексными величинами.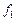 (2.30).
(2.30). , (2.31)
, (2.31) - номинальная частота,
- номинальная частота, 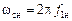 - синхронная скорость поля при номинальной частоте.
- синхронная скорость поля при номинальной частоте.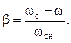 (2.32)
(2.32)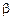 и s описывается равенством
и s описывается равенством (2.33)
(2.33)
 и относительная частота
и относительная частота 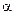 .
.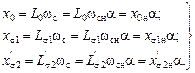 (2.34)
(2.34)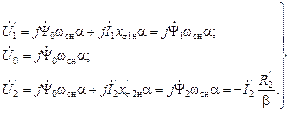 (2.35)
(2.35) соответствуют номинальной частоте. Разделив обе части уравнений (2.35) на
соответствуют номинальной частоте. Разделив обе части уравнений (2.35) на 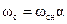 , и перейдя к действующим значениям, получим:
, и перейдя к действующим значениям, получим: (2.36)
(2.36)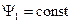 ,
,  ,
, 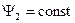 .
.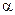 < 1) одновременно регулируют и модуль напряжения на определённом участке схемы замещения. В этом случае стабилизируется соответствующее потокосцепление.
< 1) одновременно регулируют и модуль напряжения на определённом участке схемы замещения. В этом случае стабилизируется соответствующее потокосцепление. (2.37)
(2.37)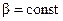 с уменьшением частоты, то есть
с уменьшением частоты, то есть 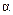 , уменьшаются все индуктивные сопротивления, что приводит к возрастанию тока статора и тока намагничивания. Это, в свою очередь, приводит к повышению степени насыщения магнитной системы. Так, если при идеальном холостом ходе уменьшить частоту в два раза, то магнитный поток
, уменьшаются все индуктивные сопротивления, что приводит к возрастанию тока статора и тока намагничивания. Это, в свою очередь, приводит к повышению степени насыщения магнитной системы. Так, если при идеальном холостом ходе уменьшить частоту в два раза, то магнитный поток 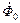 должен увеличиться в два раза, а ток намагничивания с учётом насыщении магнитопровода может увеличиться во много раз и стать больше номинального тока статора.
должен увеличиться в два раза, а ток намагничивания с учётом насыщении магнитопровода может увеличиться во много раз и стать больше номинального тока статора. зависит не только от напряжения, но и от частоты.
зависит не только от напряжения, но и от частоты. и
и 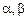 . Вторая схема относится к процессам во вращающихся системах координат:
. Вторая схема относится к процессам во вращающихся системах координат:  .
.
 ,
, 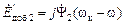 . (2.38)
. (2.38)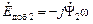 . (2.39)
. (2.39)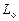 и
и  . В сумме они представляют полную индуктивность фазы статора
. В сумме они представляют полную индуктивность фазы статора 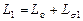 . В контуре тока ротора тоже имеется полная индуктивность
. В контуре тока ротора тоже имеется полная индуктивность 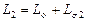 .
.

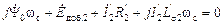 .
. .
.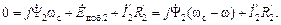
 (2.40)
(2.40) учитывается угловой частотой скольжения
учитывается угловой частотой скольжения 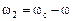 . Если в качестве переменной принимать эту частоту, то расчёт электромагнитных процессов можно выполнять без учёта механического процесса. Его можно проводить для одной фазы, не переходя к теории обобщённой электрической машины. Расчёт можно выполнять в аналитическом виде по методике предложенной в [4] или путём моделирования с помощью компьютера.
. Если в качестве переменной принимать эту частоту, то расчёт электромагнитных процессов можно выполнять без учёта механического процесса. Его можно проводить для одной фазы, не переходя к теории обобщённой электрической машины. Расчёт можно выполнять в аналитическом виде по методике предложенной в [4] или путём моделирования с помощью компьютера.
 представляет собой ЭДС самоиндукции, наведённую в статоре потокосцеплением
представляет собой ЭДС самоиндукции, наведённую в статоре потокосцеплением  , в комплексной форме записи. Во временной форме записи эта ЭДС записывается так:
, в комплексной форме записи. Во временной форме записи эта ЭДС записывается так: 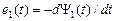 . На векторной диаграмме она действует встречно напряжению
. На векторной диаграмме она действует встречно напряжению 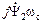 представляет собой ЭДС самоиндукции, наведённую в роторе потокосцеплением
представляет собой ЭДС самоиндукции, наведённую в роторе потокосцеплением  .
. представляет собой ЭДС вращения наводимую в роторе потокосцеплением
представляет собой ЭДС вращения наводимую в роторе потокосцеплением 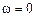 ток в роторе
ток в роторе  потребляется от источника питания. Знак минус характеризует фактическое направление тока
потребляется от источника питания. Знак минус характеризует фактическое направление тока 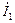 идёт на создание тока возбуждения
идёт на создание тока возбуждения 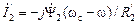 . В режиме идеального холостого хода
. В режиме идеального холостого хода  он становится равным нулю.
он становится равным нулю.
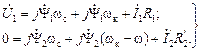 (2.41)
(2.41) - ЭДС самоиндукции, наводимые периодически изменяющимися токами статора и ротора;
- ЭДС самоиндукции, наводимые периодически изменяющимися токами статора и ротора;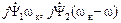 - ЭДС вращения или ЭДС взаимоиндукции с учётом взаимодействия с другими фазами. Эти ЭДС как раз и являются добавочными ЭДС (2.38).
- ЭДС вращения или ЭДС взаимоиндукции с учётом взаимодействия с другими фазами. Эти ЭДС как раз и являются добавочными ЭДС (2.38).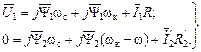 (2.42)
(2.42) . (2.43)
. (2.43)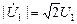 и
и  .
.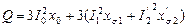 .
.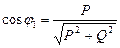 .
. .
.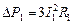 .
. и потерями мощности в активных сопротивлениях статора
и потерями мощности в активных сопротивлениях статора  принято называть эле
принято называть эле 


