
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структурная схема асинхронного двигателяСодержание книги
Поиск на нашем сайте
Структурную схему постараемся составить в таком виде, чтобы с её помощью можно было решать задачи анализа и синтеза разомкнутых и замкнутых систем. Кроме того, эта схема должна наглядно отражать сущность процессов. Процессы будем рассматривать во вращающейся системе координат
С целью сокращения числа переменных исключим токи ротора и потокосцепление статора. Из (2.54) найдём токи ротора:
С помощью этих уравнений из (2.54) находим связь между потокосцеплениями
Здесь введены обозначения:
С учётом (2.55) и (2.56) исходная система уравнений приводится к виду:
где C помощью (2.58) исключаем производные
Эти уравнения принимают более простой вид, если ЭДС, наводимую в статоре, представить в виде отдельной переменной:
С учётом (2.60) уравнения для цепей статора принимают вид:
Переходя к изображениям, получим:
Введём понятия передаточных функций для контуров статора и ротора. Они получаются из (2.58) и (2.62):
Здесь:
Выполненные преобразования позволяют изобразить структурную схему (рис.2.10). Структурная схема состоит из двух частей, одна из них отражает процессы в статоре, а другая в роторе. Первую будем называть функциональным преобразователем статора ФПС, а вторую - функциональным преобразователем ротора ФПР. Вычисление составляющих ЭДС статора по (2.60) выполняет функциональный преобразователь ЭДС. Его будем называть ФПЕ. Из схемы следует, что асинхронный двигатель представляет собой замкнутую систему пятого порядка. Система нелинейная и 2-х канальная. Нелинейность обусловлена наличием блоков произведения. Между каналами
В сумматоры 2 и 4 поступают обратные связи по ЭДС ротора. Здесь тоже важно обращать внимание на знаки. Одна из задач векторного управления сводится к компенсации имеющихся внутренних обратных связей. Влияние внутренней обратной связи по ЭДС статора можно устранить с помощью внешней обратной связи с обратным знаком. Такой приём используют и в электроприводах постоянного тока. Влияние внутренней обратной связи по ЭДС ротора можно устранить следующим образом. В сумматор с номером 4 поступают два сигнала. Допустим, что сумма этих сигналов описывается равенством:
Из структурной схемы следует, что в этом случае ось x системы координат автоматически ориентируется вдоль вектора
Решая (2.64) относительно
Таким образом, регулируя угловую частоту Отмеченное явление можно прокомментировать и иначе. Ранее было показано, что в асинхронном двигателе во всех режимах работы вектор тока Из структурной схемы следует, что при выполнении условий (2.65) потокосцепление ротора
Таким образом, при векторном управлении асинхронный двигатель может представлять собой 2-х канальную систему, в которой устранены все внутренние обратные связи. По каналу “х” регулируется составляющая тока статора
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.9.183 (0.005 с.) |

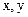 . Переходя в (2.51) и (2.52) к системе координат
. Переходя в (2.51) и (2.52) к системе координат  (2.53)
(2.53) (2.54)
(2.54) (2.55)
(2.55) и
и  :
: (2.56)
(2.56) - коэффициент электромагнитной связи ротора;
- коэффициент электромагнитной связи ротора; - переходная индуктивность статора (рис.2.9).
- переходная индуктивность статора (рис.2.9).
 – это эквивалентная индуктивность относительно клемм на входе схемы замещения на рис.2.9.
– это эквивалентная индуктивность относительно клемм на входе схемы замещения на рис.2.9. (2.57)
(2.57) (2.58)
(2.58) - постоянная времени ротора.
- постоянная времени ротора. и
и  в (2.57):
в (2.57): (2.59)
(2.59) (2.60)
(2.60) (2.61)
(2.61) (2.62)
(2.62) (2.63)
(2.63) (2.64)
(2.64) - постоянная времени статора,
- постоянная времени статора, - постоянная времени ротора.
- постоянная времени ротора. имеются внутренние перекрёстные обратные связи.
имеются внутренние перекрёстные обратные связи.
 . (2.65)
. (2.65) обращается в нуль во всех режимах работы. То есть выполняются условия:
обращается в нуль во всех режимах работы. То есть выполняются условия: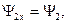
 . (2.66)
. (2.66)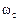 , получим:
, получим: . (2.67)
. (2.67) в соответствии с (2.67) удаётся выполнить условия (2.66). В этом случае ось х вращающейся системы координат автоматически ориентируется вдоль вектора
в соответствии с (2.67) удаётся выполнить условия (2.66). В этом случае ось х вращающейся системы координат автоматически ориентируется вдоль вектора  и полностью устраняется влияние внутренней обратной связи по ЭДС ротора.
и полностью устраняется влияние внутренней обратной связи по ЭДС ротора. ориентируется перпендикулярно вектору
ориентируется перпендикулярно вектору  . Эта особенность не зависит от закона частотного регулирования. Если выполняются условия (2.66), то реакция ротора по отношению к вектору
. Эта особенность не зависит от закона частотного регулирования. Если выполняются условия (2.66), то реакция ротора по отношению к вектору  .
. определяется лишь составляющей тока статора вдоль оси х
определяется лишь составляющей тока статора вдоль оси х . (2.68)
. (2.68) , которая создаёт потокосцепление
, которая создаёт потокосцепление  , создающая электромагнитный момент
, создающая электромагнитный момент . (2.69)
. (2.69)


