
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Схемы замещения асинхронного двигателя приСодержание книги
Поиск на нашем сайте
Постоянной частоте
Различают физическую и расчётную схему замещения. Физическая схема (рис.2.1) содержит два контура: один из них для статора, а второй для ротора.
Эта схема наглядно отражает явления, протекающие в одной из фаз статора и ротора. Однако при выполнении расчётов возникают определённые трудности, связанные с тем, что статор неподвижен, а ротор вращается со скоростью
Обратим внимание на расположение стрелок. Стрелки направлены в положительном направлении. Положительные направления назначены в соответствии с ранее отмеченным первым способом. В двигательном режиме ток статора протекает от источника питания. Вращающийся магнитный поток
Ток протекает от положительного потенциала (точка 1) к отрицательному потенциалу (точка 3). Положительные направления для напряжений При втором подходе к назначению положительных направлений для переменных поступают следующим образом. Назначают, как и ранее, положительное направление тока статора. Положительное направление для ЭДС
Рассмотренный приём обычно используют в электрических машинах постоянного тока, для которых в (2.2) отсутствует знак минус перед переменной Если в (2.2) разделить обе части второго уравнения на s, то процессы будут описываться уравнениями:
В этом случае ротор представляется неподвижным. ЭДС ротора и индуктивное сопротивление рассеяния ротора уже не зависят от скольжения. Вращение машины учитывается фиктивным сопротивлением ротора Далее, с целью упрощения расчётов, переменные и параметры ротора приводят к числу витков статора, то есть принимают
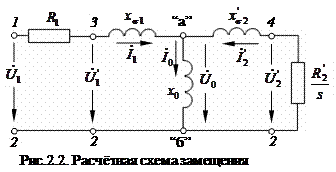
где - Для приведенных величин направление стрелок на рис.2.1 и математическое описание процессов (2.3) остаются прежними. Добавляется лишь символ штрих для переменных и параметров ротора. Так как после приведения Таким образом, с целью упрощения расчётов, выполнен переход от физической схемы замещения (рис.2.1) к расчётной схеме замещения (рис.2.2).
В этой схеме возникает электрическая связь между статором и ротором, а между точками “а” и “б” возникает цепь для протекания тока намагничивания В отличие от двигателей постоянного тока, в которых магнитный поток создается постоянным током с помощью специальной обмотки возбуждения, у асинхронных двигателей такой обмотки нет. Обмотка статора одновременно является как рабочей обмоткой, так и обмоткой возбуждения, а магнитное поле создается переменным током возбуждения
Наведенная в статоре ЭДС пропорциональна скорости изменения потокосцепления в воздушном зазоре
Последовательно переходя к току возбуждения, получим:
Напряжение для цепи намагничивания
Эти уравнения записаны для мгновенных значений переменных. Переходя к векторной форме записи, получим:
Из этих уравнений следует, что ЭДС Результирующий магнитный поток
Связь между током намагничивания и магнитным потоком характеризуется кривой намагничивания
Расчёт действующих значений ЭДС, наводимых в статоре и роторе, выполняется по (1.31), (1.33) или по формуле
По правилам общей электротехники напряжения на отдельных участках схемы замещения (рис.2.2) можно выразить через потокосцепления:
Здесь введены обозначения:
Эти понятия являются очень важными, они будут использоваться дальше и заслуживают особого внимания:
Найдём связь между токами
Здесь:
Решая (2.15) относительно токов
Отсюда можно перейти к амплитудным, а затем к действующим значениям:
Выбор той или иной схемы замещения определяется конкретно поставленной задачей и простотой приемов по достижению конечной цели. С помощью схемы на рис.2.1 проще представлять физические явления. Схема же на рис.2.2 близка к схеме замещения трансформатора и позволяет сравнительно просто устанавливать связи между переменными, выполнять расчёты, строить векторные диаграммы, и проводить анализ протекающих процессов. Связь между отдельными переменными в наглядном виде представляется с помощью векторной диаграммы (рис.2.3). Рассмотрение этой диаграммы проведём в порядке её построения. Изображается комплексная плоскость с действительной осью “+” и мнимой осью “j”. Вдоль действительной оси направим вектор тока Так как переменные ротора приведены к числу витков статора, то такая же ЭДС наводится и в роторе
Напомним, что ротор представлен неподвижным, а его вращение учитывается фиктивным сопротивлением
Вектор напряжения
Под действием ЭДС ротора протекает ток ротора
Ток Косинус этого угла
Обратите внимание, что угол Проекция вектора тока
Эта составляющая тока ротора создаёт электромагнитный момент. По известным векторам Вектор полного потокосцепления ротора с учётом полей рассеяния располагается на векторной диаграмме в соответствии с равенством
Здесь потокосцепление рассеяния ротора Потокосцепление ротора
Отсюда следует, что вектор напряжения Напряжение
На диаграмме (рис.2.3) вектора Вектор полного потокосцепления статора
Потокосцепление
Этот вектор опережает вектор Построение векторной диаграммы завершается изображением вектора напряжения
или
где В последнем уравнении напряжение
Из (2.24) и из схемы замещения (рис.2.2) следует, что если не учитывать падение напряжения в статоре
Покажем, как можно учесть влияние падения напряжения в статоре на величину потокосцепления Уравнение (2.24) с учётом (2.15) и (2.16) приводится к виду
Решая его относительно
Выполнив соответствующие действия с комплексными величинами, и осуществив переход к действующим значениям, получим [6]
где Связь между
Зависимости
При идеальном холостом ходе
В области генераторного режима (s<0) Выводы: 1. Напряжения на отдельных участках схемы замещения пропорциональны соответствующим потокосцеплениям и синхронной скорости поля 2. При идеальном холостом ходе магнитный поток через воздушный зазор пропорционален приложенному напряжению и обратнопропорционален частоте 3. При изображении схем замещения и векторных диаграмм особое внимание следует уделять расстановке направлений стрелок для переменных.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.11.13 (0.009 с.) |


 . Это приводит к тому, что переменные в статоре и роторе меняются с разными частотами. Угловая частота переменных в статоре
. Это приводит к тому, что переменные в статоре и роторе меняются с разными частотами. Угловая частота переменных в статоре 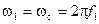 , а в роторе
, а в роторе  . ЭДС ротора и индуктивное сопротивление рассеяния ротора пропорциональны скольжению:
. ЭДС ротора и индуктивное сопротивление рассеяния ротора пропорциональны скольжению: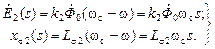 (2.1)
(2.1) наводит в статоре и роторе ЭДС вращения
наводит в статоре и роторе ЭДС вращения  ,
,  . Эти ЭДС наводятся результирующим магнитным потоком
. Эти ЭДС наводятся результирующим магнитным потоком 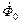 , они совпадают с направлением токов и направлены в одну сторону. Фактические направления для остальных переменных определяются режимом работы. В двигательном режиме фактическое направление
, они совпадают с направлением токов и направлены в одну сторону. Фактические направления для остальных переменных определяются режимом работы. В двигательном режиме фактическое направление  действует встречно току
действует встречно току 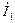 . Это учитывают следующим приёмом. Положительное направление стрелки для ЭДС
. Это учитывают следующим приёмом. Положительное направление стрелки для ЭДС 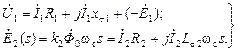 (2.2)
(2.2) направлены встречно положительному направлению ЭДС
направлены встречно положительному направлению ЭДС 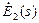 и ток ротора
и ток ротора 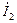 направлены согласно, то есть ЭДС ротора является источником электрической энергии для контура ротора
направлены согласно, то есть ЭДС ротора является источником электрической энергии для контура ротора можно сохранить прежнее или изменить на обратное направление. В первом случае
можно сохранить прежнее или изменить на обратное направление. В первом случае 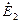 совпадало с направлением
совпадало с направлением  (2.3)
(2.3) . Частота переменных в статоре и роторе становится одинаковой
. Частота переменных в статоре и роторе становится одинаковой  .
.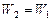 . Приведенные величины отмечают штрихом:
. Приведенные величины отмечают штрихом: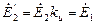 ;
; 
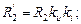
 , а коэффициенты приведения для напряжения и тока рассчитывают по формулам:
, а коэффициенты приведения для напряжения и тока рассчитывают по формулам: (2.4)
(2.4) и
и 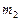 число фаз статора и ротора.
число фаз статора и ротора. и
и 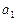 и
и 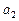 соединим. Соединим и точки
соединим. Соединим и точки 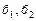 .
.
 .
.
 (2.5)
(2.5) (2.6)
(2.6) (2.7)
(2.7) (2.8)
(2.8) (2.9)
(2.9) , отстаёт от тока
, отстаёт от тока 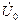 действует встречно ЭДС и опережает ток на 90 электрических градусов. С целью не загромождения рис.2.2 стрелка для ЭДС
действует встречно ЭДС и опережает ток на 90 электрических градусов. С целью не загромождения рис.2.2 стрелка для ЭДС  не приводится.
не приводится. (2.10)
(2.10) . Если насыщение не учитывается, то есть индуктивность цепи намагничивания
. Если насыщение не учитывается, то есть индуктивность цепи намагничивания 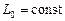 , то эта связь описывается равенством
, то эта связь описывается равенством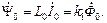 (2.11)
(2.11) (2.12)
(2.12)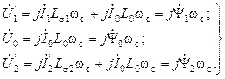 (2.13)
(2.13)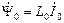 - главное потокосцепление или потокосцепление через воздушный зазор;
- главное потокосцепление или потокосцепление через воздушный зазор;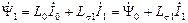 - полное потокосцепление статора с учётом полей рассеяния;
- полное потокосцепление статора с учётом полей рассеяния; - полное потокосцепление ротора с учётом полей рассеяния.
- полное потокосцепление ротора с учётом полей рассеяния.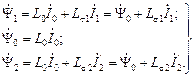 (2.14)
(2.14) (рис.2.2). Вначале выразим напряжение между точками “а” и “б” через токи
(рис.2.2). Вначале выразим напряжение между точками “а” и “б” через токи 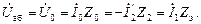 , (2.15)
, (2.15) - комплексное сопротивление контура намагничивания;
- комплексное сопротивление контура намагничивания;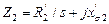 - комплексное сопротивление ротора;
- комплексное сопротивление ротора; - эквивалентное сопротивление при параллельном соединении сопротивлений
- эквивалентное сопротивление при параллельном соединении сопротивлений  и
и  .
. , находим:
, находим: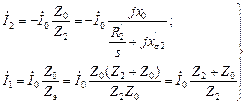 (2.16)
(2.16)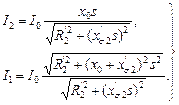 (2.17)
(2.17)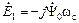 . Символ “
. Символ “  ” свидетельствует о том, что вектор
” свидетельствует о том, что вектор 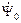 на 90 электрических градусов.
на 90 электрических градусов.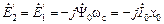 . (2.18)
. (2.18) .
.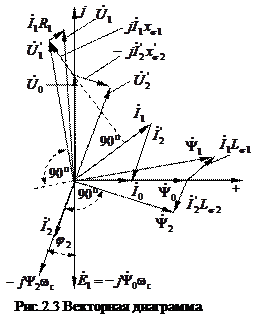
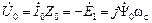 . (2.19)
. (2.19)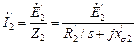 .
.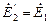 на угол
на угол 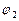 .
.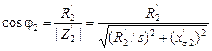 . (2.20)
. (2.20) зависит только от параметров ротора и от скольжения.
зависит только от параметров ротора и от скольжения.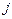 ” является активной составляющей тока ротора
” является активной составляющей тока ротора .
.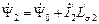 . (2.21)
. (2.21) совпадает по направлению с вектором
совпадает по направлению с вектором  наводит в роторе ЭДС. Встречно этой ЭДС действует вектор напряжения
наводит в роторе ЭДС. Встречно этой ЭДС действует вектор напряжения . (2.22)
. (2.22)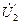 опережает вектор
опережает вектор 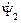 на 90 градусов и действует встречно с вектором тока
на 90 градусов и действует встречно с вектором тока  можно выразить и через напряжение
можно выразить и через напряжение  .
.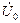 и
и 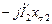 образуют треугольник.
образуют треугольник.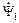 является результатом сложения векторов
является результатом сложения векторов 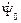 и
и 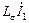
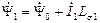 . (2.23)
. (2.23)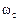 , наводит в статоре ЭДС, отстающую от вектора
, наводит в статоре ЭДС, отстающую от вектора 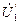
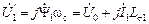 .
. часто называют напряжением за активным сопротивлением статора (рис.2.2). Символ “штрих” – это не символ приведения, он подразумевает учёт падания напряжения на активном сопротивлении статора.
часто называют напряжением за активным сопротивлением статора (рис.2.2). Символ “штрих” – это не символ приведения, он подразумевает учёт падания напряжения на активном сопротивлении статора.
 , (2.24)
, (2.24)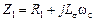 - комплексное сопротивление, учитывающее активное сопротивление и индуктивное сопротивление рассеяния статора.
- комплексное сопротивление, учитывающее активное сопротивление и индуктивное сопротивление рассеяния статора.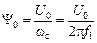 . (2.25)
. (2.25) , то уравнение (2.24) приводится к виду
, то уравнение (2.24) приводится к виду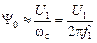 (2.26)
(2.26) .
.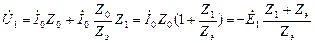 .
.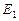 , имеем
, имеем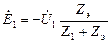 . (2.27)
. (2.27) , (2.28)
, (2.28)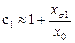 - коэффициент, характеризующий рассеяние статора. У асинхронных двигателей
- коэффициент, характеризующий рассеяние статора. У асинхронных двигателей  .
. . С учётом (2.28) получим
. С учётом (2.28) получим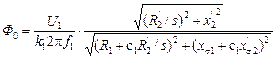 . (2.29)
. (2.29)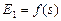 и
и  при
при 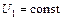 в качественном виде изображены на рис.2.4.
в качественном виде изображены на рис.2.4.
 =(0,98 ÷0,93)
=(0,98 ÷0,93)  ,
, 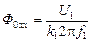 (2.30)
(2.30)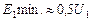 . Причина изменения
. Причина изменения 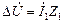 . Этот вывод следует из схем замещения. Аналогичное явление наблюдается и у двигателей постоянного тока. Отличительная особенность состоит в том, что у асинхронного двигателя все переменные являются комплексными величинами.
. Этот вывод следует из схем замещения. Аналогичное явление наблюдается и у двигателей постоянного тока. Отличительная особенность состоит в том, что у асинхронного двигателя все переменные являются комплексными величинами.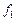 (2.30).
(2.30).


