
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модели асинхронного двигателяСодержание книги Поиск на нашем сайте
Модели бывают математические и виртуальные. В качестве примера на рис.2.12 приводится математическая модель в системе координат x,y. При составлении модели в качестве исходных данных принималась система дифференциальных уравнений (2.62) – (2.64) и структурная схема (рис.2.10). Модель состоит из двух частей. В верхней части располагаются элементы, моделирующие процессы в статоре, а в нижней части – процессы в роторе. Вычисление ЭДС, наводимой в статоре, выполняется по (2.60). Модель сложная, содержит большое количество элементов, она повторяет структурную схему и дополнена вычислениями токов ротора и потокосцеплений воздушного зазора. Предусмотрены узлы для задания начальных условий. Параметры указываются
Виртуальное моделирование [10] стало возможным с появлением современных средств вычислительной техники и пакета специализированных программ типа Matlab. Модель можно составить с помощью схем замещения на рис.2.6. Наиболее простой является модель в системе координат a, b (рис.2.13)
Модель содержит виртуальную часть и математическую. В виртуальной части для каждой фазы взята отдельная схема замещения. В пространстве эти схемы располагаются по двум взаимноортогональным осям Модель одной фазы показана в раскрытом виде. В ней на вход поступает напряжение: Для вычисления электромагнитного момента достаточно взять в каждой фазе по два тока
Дополнительные ЭДС по осям a, b вычисляются по формулам:
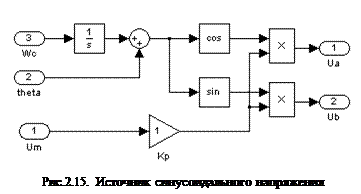
Напряжение к двигателю поступает от источника синусоидального напряжения, у которого можно регулировать амплитуду, частоту и фазу выходного напряжения, его модель приводится на рис.2.15.
Модель 3-х фазной машины (рис.2.16) содержит три блока со схемами замещения для каждой фазы. От ранее рассмотренной модели эта модель отличается наличием прямых и обратных координатных преобразователей
Модель 2-х фазной машины в системе координат
Добавочные ЭДС вводятся в статор и ротор. Они вычисляются по формулам:
Электромагнитный момент вычисляется по формуле
Если взять виртуальную часть модели и сравнить с виртуальной частью модели в системе координат Так как система координат и пространственный вектор напряжения
Здесь действительная ось комплексной плоскости совмещена с осью х. Напряжения Таким образом, при анализе процессов в системе координат х, у приходится оперировать с переменными для электрических цепей постоянного тока. Процессы представляются в более наглядном виде, управлять такими процессами проще. Это одно из достоинств модели в системе координат х, у. Виртуальная часть рассмотренных моделей содержит активные сопротивления и индуктивности. Так как параметры этих элементов в общем случае могут быть переменными и нелинейными, то при моделировании возникает потребность в составлении их моделей (рис.2.18). Модель активного сопротивления (а) содержит измеритель тока в электрической цепи, безынерционный элемент R и источник ЭДС. Здесь моделируется напряжение на активном сопротивлении для участка электрической цепи, выходная переменная описывается равенством
Модель индуктивности (б) описывает напряжение на участке электрической цепи содержащей индуктивность
Операция дифференцирования выполняется с помощью реального дифференцирующего звена. Малая постоянная времени этого звена характеризует точность моделирования. Модель нелинейной индуктивности (в) отличается от ранее рассмотренной модели наличием нелинейного звена HZ. С помощью этой модели удобно учитывать насыщение магнитной системы. Здесь напряжение для рассматриваемого участка описывается равенством, которое описывает явление электромагнитной индукции (1.1)
Система замкнутая, ток протекает под действием приложенного напряжения. Ток измеряется и его модуль формируется нелинейным звеном. В качестве нелинейного звена принимается кривая намагничивания
Здесь, в первом квадранте изображена нелинейная функция, состоящая из отрезков двух прямых. Во втором квадранте представлен отрезок синусоидальной функции Так как виртуальные модели состоят из обмоток расположенных в пространстве, то при необходимости можно проводить исследование процессов с учётом магнитной и электрической несимметрии, если таковые имеются. Характеристику “вход-выход ” нелинейного звена можно представлять не только в графическом, но и в аналитическом виде. По этому же принципу составляется модель нелинейного сопротивления.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 265; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.49.213 (0.007 с.) |



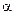 и
и 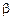 .
. . На вход второй фазы подаётся напряжение
. На вход второй фазы подаётся напряжение  .
.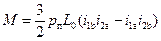 .
.

 ,
, 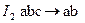 и
и  .
.
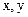 , приводится на рис.2.17.
, приводится на рис.2.17.


 .
. , то по внешнему виду они совпадают. Отличие состоит в том, что здесь в статор вводится дополнительная ЭДС. Эта особенность придаёт модели новые свойства.
, то по внешнему виду они совпадают. Отличие состоит в том, что здесь в статор вводится дополнительная ЭДС. Эта особенность придаёт модели новые свойства. вращаются с одной скоростью
вращаются с одной скоростью 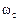 , то в этой системе координат вектор напряжения можно представить в следующих формах записи:
, то в этой системе координат вектор напряжения можно представить в следующих формах записи: .
. , поступающие на вход модели, не содержат синусоидальных функций, это напряжения для электрических цепей постоянного тока.
, поступающие на вход модели, не содержат синусоидальных функций, это напряжения для электрических цепей постоянного тока. .
.
 .
. .
. . После дифференцирования формируется напряжение на индуктивности. Получается, что потокосцепление
. После дифференцирования формируется напряжение на индуктивности. Получается, что потокосцепление  становится пропорциональным приложенному напряжению, а ток становится нелинейной функцией от приложенного напряжения. Особенность этого участка элек
становится пропорциональным приложенному напряжению, а ток становится нелинейной функцией от приложенного напряжения. Особенность этого участка элек 
 . Эта кривая пропорциональна приложенному напряжению на индуктивности. В четвёртом квадранте располагается кривая мгновенного тока. При насыщении ток становится несинусоидальным, возрастает его амплитуда, появляются дополнительные составляющие и дополнительные потери, повышающие нагрев обмотки.
. Эта кривая пропорциональна приложенному напряжению на индуктивности. В четвёртом квадранте располагается кривая мгновенного тока. При насыщении ток становится несинусоидальным, возрастает его амплитуда, появляются дополнительные составляющие и дополнительные потери, повышающие нагрев обмотки.


