
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способы распространения теплоты. Теплопроводность, количества тепла, поток тепла, плотность теплового потока.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Закон Фурье, коэффициент теплопроводности. Закон Фурье
Здесь множитель λ называется коэффициентом теплопроводности. Знак минус указывает на то, что теплота передается в направлении уменьшения температуры. Количество теплоты, прошедшее в единицу времени через единицу изотермической поверхности, называется плотностью теплового потока:
Проекции вектора q на координатные оси соответственно:
Уравнения (9.4) и (9.5) являются математическим выражением основного закона теплопроводности — закона Фурье.
Количество теплоты, проходящее в единицу времени через изотермическую поверхность F, называется тепловым потоком:
Полное количество теплоты, прошедшее через эту поверхность за время τ, определится из уравнения
Дифференциальные уравнения теплообмена. Основы теории подобия и моделирования. Критерии подобия. Критерии Нуссельта, Рейнольдса, Прандтля, Грасгофа, Архимеда,Био, Фурье. Основы теории подобия Ввиду сложности математического описания процессов конвективного теплообмена аналитическое решение дифференциальных уравнений с условиями однозначности оказывается возможным только в результате дополнительных упрощений, которые в значительной мере снижают практическую ценность полученных результатов. Поэтому многие зависимости для конкретных задач конвективного теплообмена получают экспериментальным путем. Распространение этих эмпирических зависимостей на другие конкретные явления может привести к грубым ошибкам. Объединение математических методов с экспериментом с помощью теории подобия позволяет распространить результаты единичного опыта на целую группу явлений. Понятие подобия, как известно, впервые введено в геометрии. Геометрически подобными называются такие фигуры, у которых сходственные (одноименные) стороны пропорциональны, а сходственные углы равны. Понятие подобия распространяется на любое физическое явление. Физические явления считаются подобными, если они относятся к одному и тому же классу, протекают в геометрически подобных системах, и подобны все однородные физические величины, характеризующие эти явления. Однородными называются такие величины, которые имеют один и тот же физический смысл и одинаковую размерность. Таким образом, для подобных физических явлений в сходственных точках и в сходственные моменты времени любая величина φ′ первого явления пропорциональна величине φ′′ второго явления, т. е. φ′=cφ·φ′′. При этом каждая физическая величина φ имеет свой множитель преобразования cφ′ численно отличный от других. Аналогично геометрическому подобию уравнения, описывающие подобные физические явления, после приведения их к безразмерному виду становятся тождественно одинаковыми. При этом в сходственных точках все одноименные безразмерные величины, в том числе и безразмерные параметры, будут равны. Приведем к безразмерному виду дифференциальное уравнение теплоотдачи. Если ввести обозначение ϑ=t—tc, то (10.2) можно записать в форме
Выберем какой-либо характерный геометрический размер l0 и избыточную температуру стенки ϑc=tс—tж в качестве величин приведения. Обозначим безразмерные величины и, тогда y=l0·Y и ϑ=ϑ0·θ.
Подставляя полученные выражения для у и ϑ в уравнение (10.4), запишем
Окончательно
Помимо безразмерной температуры θ и координаты Y, в уравнение входит безразмерный комплекс
Критерии, составленные из величин, определяющих характер процесса, но не включающие искомых величин, называются определяющими, а критерии, включающие искомые величины, - неопределяющими. Так, при расчёте конвективного теплообмена критерий Nu не является определяющим, так как в него входит искомая величина α. Критерии же Re и Pr в этих же расчётах – определяющие. Критерий подобия — безразмерная величина, составленная из размерных физических параметров, определяющих рассматриваемое физическое явление. Равенство всех однотипных критериев подобия для двух физических явлений и систем — необходимое и достаточное условие их физическогоподобия.
Законы теплового излучения Закон Планка устанавливает зависимость спектральной интенсивности излучения абсолютно черного тела Joλ от длины волны и температуры:
где λ — длина волны излучения, м; Т — температура излучающего тела, К; c1 =3,74·10-16 Вт·м2; c2 =1,44·10-2 м·К; e – основание натуральных логарифмов. Анализ выражения (11.12) показывает, что при λ =0 и λ =∞ Joλ =0, а при некотором промежуточном значении - имеет максимум. Для всех длин волн интенсивность излучения тем выше, чем выше температура. Максимумы кривых с повышением температуры смещаются в сторону более коротких волн. Закон Стефана — Больцмана. Плотность потока собственного интегрального излучения абсолютно черного тела можно найти на основании закона Планка как суммарную энергию излучения тела по всем длинам волн
В результате интегрирования найдём
где с0 =5,67 Вт/(м2·К4) — коэффициент излучения абсолютно черного тела. Индекс «О» указывает на то, что рассматривается излучение абсолютно черного тела. Этот закон опытным путем найден Стефаном и теоретически обоснован Больцманом задолго установления закона Планка. Спектры излучения реальных тел отличны от спектра излучения абсолютно черного тела. При этом спектральная интенсивность излучения тела на любой длине волны никогда не превышает соответствующую спектральную интенсивность излучения абсолютно черного тела. В случае селективного спектра излучения на некоторых участках длин волн интенсивность излучения равна нулю. Частным случаем реальных тел являются серые тела, спектр излучения которых подобен спектру излучения абсолютно черного тела. Интенсивность излучения для каждой длины волны серого тела Jλ составляет одну и ту же долю интенсивности излучения черного тела J0λ, то есть
Здесь величина ε — степень черноты тела, зависящая от физических свойств тела, но всегда ε <1. Большинство реальных тел с определенной степенью точности можно считать серыми. Закон Стефана — Больцмана для серого тела с учетом выражения (11.15) имеет вид:
где с — коэффициент излучения серого тела. Излучение газов Одно- и двухатомные газы практически прозрачны для теплового излучения. Значительной излучающей и поглощающей способностью, имеющей практическое значение, обладают трех- и многоатомные газы. Для теплотехнических расчетов наибольший интерес представляют углекислый газ и водяной пар, образующийся при горении топлива. В отличие от твердых тел, имеющих в большинстве сплошные спектры излучения, газы излучают энергию лишь в определенных интервалах длин волн Δλ, называемых полосами спектра. Для лучей других длин волн вне этих полос газы прозрачны, и их энергия излучения равна нулю. Таким образом, излучение и поглощение газов имеют избирательный характер. Если поглощение и излучение энергии в твердых телах происходят в тонком поверхностном слое, то газы излучают и поглощают энергию во всем объеме. Количество поглощаемой газом энергии зависит от числа находящихся в данном объеме микрочастиц газа. Последнее пропорционально толщине газового слоя, характеризуемой длиной пути луча l, парциальному давлению газа р и его температуре Т. Следовательно,
Плотность интегрального излучения газовой среды определится суммой их значений для отдельных полос, то есть
Отсюда следует, что законы излучения газов значительно отклоняются от закона Стефана — Больцмана. Однако в основу практических расчетов излучения газов положен именно этот закон. В итоге плотность интегрального излучения с поверхности газового слоя определяется уравнением
где εг — степень черноты газа при температуре газа Тг; Аг — поглощающая способность газа при температуре оболочки Тст; Рисунок 1. Передача теплоты через плоскую стенку: а - однослойную; б - многослойную Из закона распространения теплоты путем теплопроводности (закона Фурье) следует:
где W - количество переданной теплоты, Дж; λ - коэффициент пропорциональности, называемый коэффициентом теплопроводности, Вт/(м·К); tсl - температура одной поверхности стенки, К; tсll - температура другой поверхности стенки, К; δ - толщина стенки, м; F - площадь поверхности стенки, м2; τ - время, с. Отсюда
т.е. коэффициент теплопроводности численно равен количеству теплоты, которое проходит в единицу времени (1с) в теле через единицу поверхности (1 м2) при падении температуры на 1 К на 1 м пути теплового потока. Если обе части уравнения (3) разделить на Ft, to получим
или
где δ/λ - термическое сопротивление теплопроводности. Таким образом, плотность теплового потока q прямо пропорциональна разности температур на поверхностях стенки и обратно пропорциональна термическому сопротивлению теплопроводности. Коэффициент теплопроводности λ у различных материалов неодинаков и зависит от их свойств, а у газообразных и жидких веществ - от плотности, влажности, давления и температуры этих веществ. При технических расчетах значения λ выбирают по соответствующим справочным таблицам. Рассмотрим теперь процесс передачи теплоты через многослойную стенку. На рис. 1, б изображена плоская стенка, состоящая из трех слоев, указаны промежуточные температуры на границах этих слоев, а также толщина слоев и значения коэффициентов теплопроводности для каждого слоя. При стационарном режиме тепловой поток, проходящий через каждый отдельный слой, будет один и тот же. Тогда для каждого слоя в соответствии с формулой (6) можно записать:
Отсюда
Сложив правые и левые части этих уравнений, получим:
Следовательно, плотность теплового потока многослойной стенки
Из записанных уравнений для трех разностей температур можно получить формулы для вычисления промежуточных температур. Например:
и
СЛОЖНЫЙ ТЕПЛООБМЕН. Рассмотренные выше явления передачи теплоты протекают обычно одновременно. Например, когда тело (поверхность нагрева) омывается газом, то наряду с конвективным теплообменом имеется теплообмен излучением (радиацией). В системах отопления, вентиляции и кондиционирования наиболее часто встречающийся случай теплообмена - это передача теплоты от греющей жидкости, нагреваемой среде (воздух, жидкость) через разделительную стенку (рис. 2, а). В этом случае вначале происходит теплоотдача от греющей жидкости со средней температурой t1 стенке с температурой tcl. Далее теплота передается в результате теплопроводности стенки ее противоположной поверхности с температурой tcll и, наконец, эта поверхность стенки отдает теплоту нагреваемой среде со средней температурой t2. Тогда плотность теплового потока для однослойной стенки с учетом формул (6) и (10) будет
где α1 - коэффициент теплоотдачи от греющей жидкости левой (см. рис. 2, а) поверхности стенки; δ - толщина стенки; λ - коэффициент теплопроводности разделительной стенки; α2- коэффициент теплоотдачи от правой поверхности стенки, нагреваемой среде.
Рисунок 2. Передача теплоты от греющей жидкости, нагреваемой среде через разделительную стенку: а - однослойную; б - многослойную Если дробь
обозначить буквой k, то формула для подсчета количества теплоты, передаваемой через площадь F за время τ, примет следующий вид:
Величину k называют коэффициентом теплопередачи [измеряется в Вт/(м2·К)], а обратную ему величину - полным термическим сопротивлением теплопередачи R0 = 1/k = 1/α1 + δ/λ + 1/α2. Если разделительная стенка состоит из нескольких слоев, например из трех (рис. 2, б), то плотность теплового потока с учетом формул (7) и (10) будет
а коэффициент теплопередачи
В многочисленных теплообменных устройствах, применяемых в любой области промышленности, в том числе в системах отопления, вентиляции и кондиционирования, основным рабочим процессом является теплообмен между теплоносителями. Такой теплообмен называют теплопередачей. Способы распространения теплоты. Теплопроводность, количества тепла, поток тепла, плотность теплового потока. Теплообменом называется перенос тепла от одних тел к другим или одних частей тела к другим, вызываемый разностью температур. Процесс теплообмена – это сложный процесс, он связан с конвективной и молекулярной диффузией и определяется законами аэродинамики, газодинамики, термодинамики, передачи энергии в форме теплоты, передачи лучистой энергии и превращением ее в теплоту и наоборот. Теплообмен характеризуется выравниванием температуры и осуществляется тремя способами: теплопроводностью, конвекцией, излучением. Теплопроводность – это передача тепла молекулярной диффузией, т.е. перенос тепловой энергии осуществляется от частиц обладающих большей энергией к частицам с меньшей энергией. Теплопроводность наблюдается только в твердых телах и неподвижных слоях жидкости или газа. Конвекция – передача тепла потоками жидкости или газа из одной области пространства в другую. Конвекция бывает свободной и вынужденной. Свободная конвенция возникает из-за разности плотностей нагретой и холодной среды. При вынужденной конвенции движущиеся потоки создаются принудительно – компрессором, вентилятором и т.д. Конвекция сопровождается переносом тепла теплопроводностью в пограничных слоях. Совместный процесс конвекции и теплопроводности называется конвективным теплообменом. Излучение – это передача тепловой энергии путем электромагнитных колебаний. Процесс передачи тепла излучением можно условно разделить на 3 этапа: 1. Преобразование внутренней энергии системы в энергию электромагнитных волн; 2. Распространение этих волн в среде, разделяющей источник и приемник. 3.Реакция приемника на излучение. В реальных условиях названные способы переноса тепла протекают одновременно: такое физическое явление называется сложным теплообменом. Его закономерности могут быть установлены на основе закономерностей простых видов теплообмена. Тепловой поток – это количество тепловой энергии, которая передается через произвольную поверхность в единицу времени:
Удельный тепловой поток – это количество тепловой энергии, которая передается через 1 м2 поверхности за единицу времени:
где F – площадь поверхности, м2; Ф – тепловой поток, Вт . 2.2 Теплопроводность Если выделить в теле слой толщиной dх, то через площадку dF, нормальную к направлению теплового потока, за время
где
dF - площадь, м2. Дифференциальная зависимость (2.3) называется основным уравнением теплопроводности или уравнением Фурье
Рис. 2.1 Схема переноса тепла через плоскую однородную стенку. Величина
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 722; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.014 с.) |

 Согласно гипотезе Фурье, количество теплоты d2Qτ, проходящее через элемент изотермической поверхности dF за промежуток времени dτ, пропорционально температурному градиенту
Согласно гипотезе Фурье, количество теплоты d2Qτ, проходящее через элемент изотермической поверхности dF за промежуток времени dτ, пропорционально температурному градиенту  :
:



 .
.




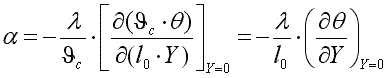

 , составленный из разнородных физических величин, характеризующих явление теплоотдачи. Согласно свойству подобных физических явлений, этот комплекс должен иметь одинаковые значения для всех подобных систем. Такие комплексы носят название чисел подобия. Полученный безразмерный комплекс называется числом Нуссельта
, составленный из разнородных физических величин, характеризующих явление теплоотдачи. Согласно свойству подобных физических явлений, этот комплекс должен иметь одинаковые значения для всех подобных систем. Такие комплексы носят название чисел подобия. Полученный безразмерный комплекс называется числом Нуссельта  и представляет собой безразмерный коэффициент теплоотдачи. Числа подобия, составленные только из заданных параметров математического описания задачи, называются критериями подобия. Анализ уравнений конвективного теплообмена позволяет получить следующие основные критерии подобия:
и представляет собой безразмерный коэффициент теплоотдачи. Числа подобия, составленные только из заданных параметров математического описания задачи, называются критериями подобия. Анализ уравнений конвективного теплообмена позволяет получить следующие основные критерии подобия: — критерий Рейнольдса, характеризующий режим движения жидкости;
— критерий Рейнольдса, характеризующий режим движения жидкости; — критерий Грасгофа, характеризующий подъемную силу, возникшую вследствие разности плотности жидкости. Здесь β - коэффициент объёмного расширения жидкости;
— критерий Грасгофа, характеризующий подъемную силу, возникшую вследствие разности плотности жидкости. Здесь β - коэффициент объёмного расширения жидкости; — критерий Прандтля, определяющий физические свойства жидкости.
— критерий Прандтля, определяющий физические свойства жидкости.


 ,
,

 ,
,

 ,
,

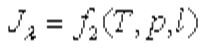
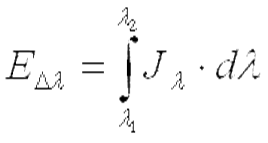
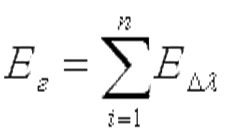
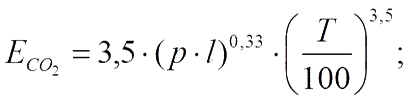
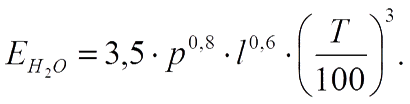
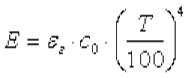
 ,
,
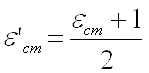 — эффективная степень черноты оболочки.
— эффективная степень черноты оболочки.















 ,
,  (2.1)
(2.1) ,
,  (2.2)
(2.2) пройдет количество теплоты, равное
пройдет количество теплоты, равное , (2.3)
, (2.3) – коэффициент теплопроводности, Вт/м·К
– коэффициент теплопроводности, Вт/м·К  ;
; – разность температур в слое, К;
– разность температур в слое, К; – толщина слоя, м;
– толщина слоя, м;
 показывает изменение температуры в слое
показывает изменение температуры в слое 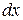 и называется градиентом температур. Распространение тепла в теле происходит лишь в сторону понижения температуры, поэтому величина
и называется градиентом температур. Распространение тепла в теле происходит лишь в сторону понижения температуры, поэтому величина  отрицательна, на что показывает знак минус в уравнении Фурье.
отрицательна, на что показывает знак минус в уравнении Фурье.


