Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Б1. 35. Фундаментальная последовательностьСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Фундаментальная последовательность (последовательность Коши, сходящаяся в себе последовательность) – последовательность{ xn }, удовлетворяющая следующему условию Коши: Для любого ε > 0 существует такое n, что для всех n > N, m > N выполняется неравенство |xn – xm| < ε. Здесь xn – действительное или комплексное число или точка метрического пространства, | xn – xm | – расстояние между числами xn и xm или между точками xn и xm этого пространства. Любая сходящаяся последовательность фундаментальна. Пространство, в котором верно и числа обратное утверждение, называется полным. Множество действительных чисел и множество комплексных чисел – примеры полных пространств, а, скажем, множество рациональных чисел – нет: последовательность рациональных значений Задание. Доказать сходимость последовательности Доказательство. Покажем вначале, что заданная последовательность является фундаментальной, то есть для любого
Таким образом, для любого Б1. 36. Полное метрическое пространство Полное метрическое пространство – метрическое пространство, в котором каждая фундаментальная последовательность сходится (к элементу этого же пространства). В большинство случаев рассматривают именно полные метрические пространства. Для неполных пространств существует операция пополнения, дающая возможность рассматривать исходное пространство как плотное множество в своем пополнении. Операция пополнения во многом аналогична операции замыкания для подмножеств. Пополнение. Всякое метрическое пространство Построение. Для метрического пространства
Можно классов эквивалентности – с метрикой, определенной
является метрическим пространством. Само пространство Свойства: · Пополнение метрического пространства единственно, с точностью до изометрии. · Полнота наследует замкнутыми подмножествами полного метрического пространства. · Метрическое пространство · Топологическим свойством является наличие хотя бы одной полной метрики в классе метрик, порождающих топологию метрического пространства Примеры: · Множество вещественных чисел
· Вообще, любое конечномерное евклидово или унитарное пространство полно · Свойство полноты является обязательным в определении банахова пространства, в частности гильбертова пространства. · Пространство непрерывных на отрезке функций с равномерной метрикой является полным метрическим пространством, а потому является банаховым, если рассматривать его как нормированное линейное пространсво. Б1. 37.Компактное множество Определение. Пусть множество Определение. Множеств Например, множество, состоящее из одной точки, двух точек или любого конечного набора точек, очевидно, компактное. Пусть diam Лемма (о вложенности сегментах). Пусть Доказательство. Пусть
|
||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 829; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |

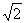 , взятых с недостатком (т.е. последовательность 1; 1,4; 1,41; …), сходится, но её предел не является рациональным числом.
, взятых с недостатком (т.е. последовательность 1; 1,4; 1,41; …), сходится, но её предел не является рациональным числом. , используя критерий Коши.
, используя критерий Коши.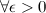 ,
, 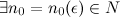 :
: 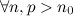 :
: 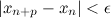 :
: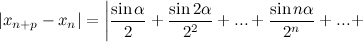
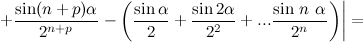

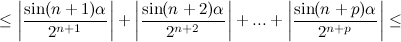
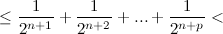


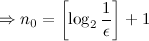
 , а значит рассматриваемая последовательность является фундаментальной, а тогда по критерию Коши она является сходящейся.
, а значит рассматриваемая последовательность является фундаментальной, а тогда по критерию Коши она является сходящейся.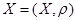 можно вложить в полное метрическое пространство
можно вложить в полное метрическое пространство 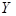 таким образом, что метрика – продолжает метрику Х, а подпространство Х всюду плотно в
таким образом, что метрика – продолжает метрику Х, а подпространство Х всюду плотно в 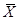 .
.
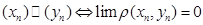
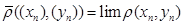 ,
,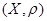 изометрически вкладывается в него следующим образом: точке
изометрически вкладывается в него следующим образом: точке  соответствует класс постоянной последовательности
соответствует класс постоянной последовательности  . Получившееся пространство
. Получившееся пространство 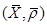 и будет пополнением
и будет пополнением 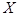 компактно тогда и только тогда, когда оно полно и вполне ограничено, то есть для любого
компактно тогда и только тогда, когда оно полно и вполне ограничено, то есть для любого 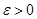 пространство
пространство 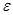
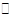 полно в стандартной метрике
полно в стандартной метрике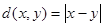
 . Семейство открытых множеств
. Семейство открытых множеств 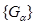 называется открытым покрытием множества Е, если каждая точка
называется открытым покрытием множества Е, если каждая точка  принадлежит хотя бы одному из множеств
принадлежит хотя бы одному из множеств 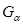 , т.е. если
, т.е. если 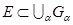 .
. , т.е. верхняя грань расстояний между всевозможными парами точек из Е. Например, если
, т.е. верхняя грань расстояний между всевозможными парами точек из Е. Например, если 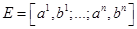 -
- 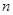 - мерный сегмент, то, diam
- мерный сегмент, то, diam  ,где
,где 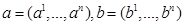 .
.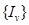 - последовательность вложенных сегментов из
- последовательность вложенных сегментов из  , т.е.
, т.е. 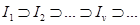 , диаметры которых стремится к нулю при
, диаметры которых стремится к нулю при 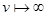 . Тогда существует, и притом единственная, точка
. Тогда существует, и притом единственная, точка 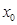 , принадлежащая всем этим сегментам.
, принадлежащая всем этим сегментам.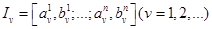 .При каждом фиксированном
.При каждом фиксированном  последовательность одномерных отрезков
последовательность одномерных отрезков  состоит из вложенных друг в друга отрезков, т.е.
состоит из вложенных друг в друга отрезков, т.е. 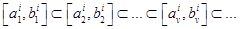 б и длины этих отрезков стремятся к нулю при
б и длины этих отрезков стремятся к нулю при 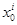 такое, что
такое, что 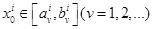 , т.е.
, т.е.  .Но тогда точка
.Но тогда точка 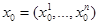 , очевидно, принадлежит всем
, очевидно, принадлежит всем 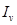 . Двух различных точек, принадлежащих всем
. Двух различных точек, принадлежащих всем 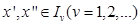 , то
, то 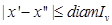 . По условию правая часть стремится к нулю при
. По условию правая часть стремится к нулю при