
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Б1. 25. Интеграл римана и Лебега
Пусть на отрезке [a,b] определена вещественнозначная f. Рассмотрим разбиение отрезка a=x0<x1<x2<... <xт-1<xт=b — конечное множество попарно различных точек отрезка. Это разбиение делит отрезок [a,b] на n отрезков [xi-1,xi], i=1... n. Длина наибольшего из отрезков δR=max(Δ xi)называется шагом разбиения, где Δxi = xi-xi-1— длина элементарного отрезка. Отметим на каждом отрезке разбиения по точке ξi∋[xi-1,xi]. Интегральной суммой называется выражение Если при стремлении шага разбиения к нулю интегральные суммы стремятся к одному и тому же числу, независимо от выбора ξi∋[xi-1,xi], то это число называется интегралом функции f на отрезке [a,b], то есть В этом случае, сама функция f называется интегрируемой (по Риману) на [a,b].
Понятие интеграла Римана не пременимо для измеримых функций, которые могут быть разрывны во всей области определения или заданы на таком абстрактном множестве, что понятие интегральных сумм не имеет смысла. В отличие от интеграла Римана, основная идея интеграла Лебега состоит в том, что точки группируются по признаку близости значений функции в этих точках. 26,27,28,29,30
Б1. 31. Замыкание множества. Предельная точка Замыкание множества Определение 8.1. Точка х называется точкой прикосновения множества А Совокупность всех точек прикосновения множества А называется замыканием множества А и обозначается А с чертой. Операция перехода от множества А к множеству называется операцией замыкания. Любая точка множества А является его точкой прикосновения, но есть точки прикосновения, которые не принадлежат множеству А. Так, например, замыканием интервала (a, b) является отрезок [ a, b ], замыканием открытого шара в R n - замкнутый шар (вместе с ограничивающей его сферой). Замыкание множества Q рациональных чисел на прямой совпадает со всей числовой прямой:. Из определения замыкания следует также, что замыкание пустого множества пусто, а замыкание всего пространства Х совпадает с Х. Операция замыкания обладает также свойствами: 1. M 2. Если M 3. (идемпотентность). Предельная точка множества. Предел функции в точке Пусть
Из определения следует, что любая окрестность точки x 0 содержит точку из множества X, отличную от x 0. Сама точка x 0 может принадлежать, а может и не принадлежать множеству X. Значение +∞ есть предельная точка множества X, если
Значение -∞ предельная точка множества X, если
Число
|
|||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 356; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.129.19 (0.004 с.) |
 .
. .
.
 (Х, τ), если любая ее окрестность имеет непустое пересечение с А.
(Х, τ), если любая ее окрестность имеет непустое пересечение с А. . Число
. Число  называется предельной точкой множества X, если
называется предельной точкой множества X, если

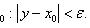





 называется предельной точкой множества
называется предельной точкой множества  , если из этого множества можно выделить последовательность (xn) различных точек, сходящуюся к x 0. (Данное определение и определение, указанное в самом начале эквивалентны)
, если из этого множества можно выделить последовательность (xn) различных точек, сходящуюся к x 0. (Данное определение и определение, указанное в самом начале эквивалентны)


