
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Б1. 16 Равномерная сходимость функциональных последовательностей и рядов
Определение 1. Функциональная последовательность (31.1) называется равномерно сходящейся к функции f на множестве X, если для любого
Очевидно, что если последовательность (31.1) равномерно сходится на множестве X к функции f, то эта последовательность сходится к функции f на рассматриваемом множестве (определение сходимости последовательности функций на множестве). Если последовательность { fn } сходится на множестве X к функции f, то пишут fn а если эта последовательность сходится равномерно к f на указанном множестве, то пишут fn В символической записи определения сходящейся и равномерно сходящейся на множестве последовательности выглядят соответственно следующим образом: fn fn
Таким образом, если последовательность { fn } только сходится к функции f на множестве X, то для каждой точки x | fn (x) - f (x)| < и может оказаться, что для всех точек x Лемма 1. Для того чтобы последовательность { fn } равномерно сходилась на X к функции f, необходимо и достаточно, чтобы
Значение этой леммы состоит в том, что она сводит понятие равномерной сходимости поледовательности { fn } функций к понятию сходимости числовой последовательности { ("числовой" в широком смысле этого слова: конечное число членов указанной последовательности может обратиться в + fn Зададим произвольно
Это и означает выполнение условия (31.8).
а следовательно, для всех n > n 0 и всех x | fn (x) - f (x)| < Это означает, что fn Следствие. Если существует стремящаяся к нулю последовательность {
такая, что для всех x
то последовательность { fn (x)} равномерно сходится к функции f (x) на множестве X.
а поэтому из условия
Замечание 1. Очевидно, что из определения равномерной сходимости последовательности функций следует, что если какие-то последовательности равномерно сходятся на некотором множестве, то и любая их конечная линейная комбинация равномерно сходится на этом множестве. Б1. 17 ЛЕБЕГА ИНТЕГРАЛ Одноиз наиболее важных обобщений понятия интеграла. Пусть
сходится абсолютно; сумма этого ряда есть интеграл Лебега:
Функция
конечен. Число I есть интеграл Лебега:
Определение корректно: предел I существует и не зависит от выбора последовательности gn. Если
В случае, когда
интеграл Лебега
определяется как
при условии, что этот предел существует и конечен для любой последовательности Е п такой, что
определяется или, как указано выше, заменой Xна А, или как
где
Обратно, если при тех же условиях на А n для каждого
то Функция множества
абсолютно непрерывна относительно Для функций
Для других мер этот функционал наз. Лебега-Стилтьеса интегралом. Если
Если
-мо- нотонна на
и существует точка
такая, что
(вторая теорема о среднем). А. Лебег дал в 1902 (см. [1]) определение интеграла для
Б1. 18 Интеграл Лебега от ограниченной функции
Пусть действительная функция y = f (x) измерима и ограничена на ограниченном интервале [ a, b ] и A и B - соответственно ее нижняя и верхняя точные границы. Разобъем интервал [ A, B ], содержащий множество значений функции f (x) на [ a, b ], на n частей: A = y 0 < y 1 < y 2 <... < yn = B, и обозначим через Si множество точек x интервала [ a, b ], в которых
Обе интегральные суммы стремятся к одному и тому же пределу, не зависящему от выбора значений yi, если только наибольшая из разностей yi - yi -1 стремится к нулю. Число
есть определенный интеграл от функции f (x) по интервалу [ a, b ] в смысле Лебега (интеграл Лебега). Это определение означает, что, каково бы ни было положительное число
а значит, и неравенство
где
Б1. 19 Интеграл Лебега Пусть
Опр. Ф-ция Свойства интеграла Лебега: 1. Если Поскольку 2. Если 3. Пусть 4. Счетная аддитивность интеграла Лебега: Пусть 5. Абсолютная непрерывность интеграла Лебега: Если Заметим, что Ввиду аналогичного свойства для неотрицательных функций имеем, что
Для этого же Выберем 6. Если ф-ция Если ф-ции
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 266; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.22.244 (0.048 с.) |
 > 0 существует такой номер n 0, что для всех точек x
> 0 существует такой номер n 0, что для всех точек x  X и всех номеров n > n 0 выполняется неравенство
X и всех номеров n > n 0 выполняется неравенство f,
f, f.
f.

 n 0
n 0  Рис. 124
Рис. 124

 | fn (x) - f (x)| = 0.
| fn (x) - f (x)| = 0.
 ). В силу этого обстоятельства условие (31.8) часто бывает удобно использовать для выяснения, сходится ли равномерно интересующая нас конкретная последовательность функций.
). В силу этого обстоятельства условие (31.8) часто бывает удобно использовать для выяснения, сходится ли равномерно интересующая нас конкретная последовательность функций. 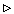 1. Пусть
1. Пусть | fn (x) - f (x)| <
| fn (x) - f (x)| < 
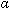 n }:
n }: - пространство с неотрицательной полной счетно аддитивной мерой
- пространство с неотрицательной полной счетно аддитивной мерой  причем
причем  Простой ф у н к ц и е й наз. измеримая функция
Простой ф у н к ц и е й наз. измеримая функция  принимающая не более счетногомножества значений:
принимающая не более счетногомножества значений: 
 Простаяфункция gназ. суммируемой, если ряд
Простаяфункция gназ. суммируемой, если ряд

 суммируема на
суммируема на  если существует равномерно сходящаяся намножестве полной меры к f последовательность простых суммируемых функций gn и предел
если существует равномерно сходящаяся намножестве полной меры к f последовательность простых суммируемых функций gn и предел

 то I - измеримая почти всюду конечная функция на X. Л. и. есть линейный неотрицательныйфункционал на
то I - измеримая почти всюду конечная функция на X. Л. и. есть линейный неотрицательныйфункционал на  обладающий следующими свойствами:
обладающий следующими свойствами:




 В этом случае свойства 1), 2), 3) сохраняются, а свойство 4) нарушается. Опереходе к пределу под знаком Л. и. см. Лебега теорема. Если Аесть измеримое множество X, то Л. и.
В этом случае свойства 1), 2), 3) сохраняются, а свойство 4) нарушается. Опереходе к пределу под знаком Л. и. см. Лебега теорема. Если Аесть измеримое множество X, то Л. и.

 - характеристич. функция А;эти определения эквивалентны. Если
- характеристич. функция А;эти определения эквивалентны. Если  для любого измеримого
для любого измеримого  Если
Если
 измеримо для каждого п, для
измеримо для каждого п, для 

 и
и
 и верно предыдущее равенство (
и верно предыдущее равенство ( -аддитивность Л. и.).
-аддитивность Л. и.).

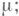 если
если  то F(А).есть неотрицательная абсолютно непрерывнаяотносительно
то F(А).есть неотрицательная абсолютно непрерывнаяотносительно  мера. Обратное утверждение представляет Радона - Никодима теорему.
мера. Обратное утверждение представляет Радона - Никодима теорему. название "интеграл Лебега" применяется к соответствующему функционалу, если мера
название "интеграл Лебега" применяется к соответствующему функционалу, если мера  есть Лебега мера;при этом множество суммируемых функций обозначается просто L(Х).иинтеграл
есть Лебега мера;при этом множество суммируемых функций обозначается просто L(Х).иинтеграл
 - неубывающая абсолютнонепрерывная функция, то
- неубывающая абсолютнонепрерывная функция, то

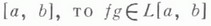


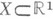 и меры
и меры  являющейся мерой Лебега. Онстроил простые функции, равномерно приближающие почти всюду на множестве конечной мерыЕизмеримую неотрицательную функцию
являющейся мерой Лебега. Онстроил простые функции, равномерно приближающие почти всюду на множестве конечной мерыЕизмеримую неотрицательную функцию  и доказал существование общего предела(конечного или бесконечного) интегралов этих простых функций при стремлении их к f. Л. и. является базойдля различных обобщений понятия интеграла. Как отметил Н. Н. Лузин [2], свойство 2) - т. н. абсолютнаяинтегрируемость, выделяет Л. к. для
и доказал существование общего предела(конечного или бесконечного) интегралов этих простых функций при стремлении их к f. Л. и. является базойдля различных обобщений понятия интеграла. Как отметил Н. Н. Лузин [2], свойство 2) - т. н. абсолютнаяинтегрируемость, выделяет Л. к. для  из всевозможных обобщенных интегралов.
из всевозможных обобщенных интегралов.
 . Составим две суммы (интегральные суммы Лебега):
. Составим две суммы (интегральные суммы Лебега):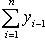
 и
и 
 .
.



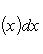
 , можно указать такое число
, можно указать такое число  , что при любом разбиении интервала [ A, B ] на части такие, что
, что при любом разбиении интервала [ A, B ] на части такие, что 
 , будут справедливы неравенства
, будут справедливы неравенства
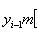
 и
и 

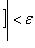 ,
,



 (интеграл Лебега можно определить и как предел суммы
(интеграл Лебега можно определить и как предел суммы 
 ).
).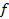 измерима на
измерима на  .
.  ф-ции
ф-ции  .
.
 , а число
, а число  наз.интегралом Лебега от ф-ции
наз.интегралом Лебега от ф-ции  и
и 
 на
на 
 и
и 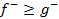 и
и 

 - интегрируема на
- интегрируема на  на
на  имеем
имеем  и
и 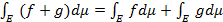
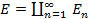 ,
,  измеримые множества. Тогда
измеримые множества. Тогда  , причем ряд абсолютно сходится.
, причем ряд абсолютно сходится.
 .
.

 так, чтобы
так, чтобы  (отсутствие такого
(отсутствие такого 
 п.в. на
п.в. на 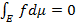
 , то
, то  (док-во этого факта от противного). Следовательно, имеем
(док-во этого факта от противного). Следовательно, имеем  на основании свойства для неотрицательных функций.
на основании свойства для неотрицательных функций. ,
,  - неотрицательны.)
- неотрицательны.)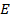 , то, очевидно, свойство выполнено. (ввиду того, что множество на которых у
, то, очевидно, свойство выполнено. (ввиду того, что множество на которых у 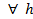 - простую на
- простую на  . Полагая ее равной 0 на
. Полагая ее равной 0 на 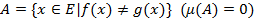 . Переходя к функции равной
. Переходя к функции равной  п.в., получили функцию
п.в., получили функцию  . Ввиду того, что по предыдущему пункту
. Ввиду того, что по предыдущему пункту  , тогда т.в.г. у множеств из определения интеграла Лебега от неотрицательной функции для
, тогда т.в.г. у множеств из определения интеграла Лебега от неотрицательной функции для 


