
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Б1. 1. Множество. Подмножество. Равные множества. Пустое множество. Объединение, пересечение, разность, симметрическая разность множеств. Дизъюктные множества.Стр 1 из 5Следующая ⇒
Б1. 1. Множество. Подмножество. Равные множества. Пустое множество. Объединение, пересечение, разность, симметрическая разность множеств. Дизъюктные множества.
Б1. 2. Сравнение множеств. Мощность. Примеры.
Б1. 3. Взаимооднозначное соответствие между множествами.
Б1. 4. Множества меры нуль. Мера пустого множества.
Б1. 5. Свойства внешней меры.
Б1. 6. Измеримые множества Б1. 7. Операции над измеримыми множествами
Б1. 8. Измеримые функции. Теоремы о функции, заданной на множестве меры нуль и равной константе.
Б1. 9. Арифметические операции над измеримыми функциями
Б1. 10. Эквивалентные функции Определение 4. Функция f называется эквивалентной функции g (или асимптотически равной ей) при x
В этом случае пишут f ~ g, x Замечание 1. Если x 0
Замечание 2. Если в условиях определений 3 или 4 функция g не обращается в нуль на множестве x
а условие (9.26) - в виде
Замечание 3. Если x 0
то функция f (x)/ g (x) ограничена на пересечении некоторой окрестности U (x 0) точки x 0 с множеством X т. е. существует такая постоянная c > 0, что для всех x откуда следует, что при выполнении условия (9.29) имеет место соотношение f (x) = O (g (x)), x Теорема 1. Для того чтобы функции f (x) и g (x) были эквивалентны при x
Б1. 11. Эквивалентность непрерывных функций
Б1. 12. Определение свойства почти всюду
Б1. 13. Сходимость почти всюду
Б1. 14. Простые функции
Б1. 15. Интеграл Лебега простой функции Мы введем понятие интеграла Лебега сначала для функций, названных выше простыми, т. е. для измеримых функций, принимающих конечное или счетное число значений.
Б1. 21. Теорема Леви
Б1. 22. Лемма Фату
Б1. 23. 24. Теорема Лебега
Б1. 31. Замыкание множества. Предельная точка Замыкание множества Определение 8.1. Точка х называется точкой прикосновения множества А Совокупность всех точек прикосновения множества А называется замыканием множества А и обозначается А с чертой. Операция перехода от множества А к множеству называется операцией замыкания. Любая точка множества А является его точкой прикосновения, но есть точки прикосновения, которые не принадлежат множеству А. Так, например, замыканием интервала (a, b) является отрезок [ a, b ], замыканием открытого шара в R n - замкнутый шар (вместе с ограничивающей его сферой). Замыкание множества Q рациональных чисел на прямой совпадает со всей числовой прямой:. Из определения замыкания следует также, что замыкание пустого множества пусто, а замыкание всего пространства Х совпадает с Х. Операция замыкания обладает также свойствами: 1. M 2. Если M 3. (идемпотентность). Предельная точка множества. Предел функции в точке Пусть
Из определения следует, что любая окрестность точки x 0 содержит точку из множества X, отличную от x 0. Сама точка x 0 может принадлежать, а может и не принадлежать множеству X. Значение +∞ есть предельная точка множества X, если
Значение -∞ предельная точка множества X, если
Число
Пополнение. Всякое метрическое пространство Построение.
Для метрического пространства
Можно классов эквивалентности – с метрикой, определенной
является метрическим пространством. Само пространство Свойства: · Пополнение метрического пространства единственно, с точностью до изометрии. · Полнота наследует замкнутыми подмножествами полного метрического пространства. · Метрическое пространство · Топологическим свойством является наличие хотя бы одной полной метрики в классе метрик, порождающих топологию метрического пространства Примеры: · Множество вещественных чисел
· Вообще, любое конечномерное евклидово или унитарное пространство полно · Свойство полноты является обязательным в определении банахова пространства, в частности гильбертова пространства. · Пространство непрерывных на отрезке функций с равномерной метрикой является полным метрическим пространством, а потому является банаховым, если рассматривать его как нормированное линейное пространсво. Б1. 37.Компактное множество Определение. Пусть множество Определение. Множеств Например, множество, состоящее из одной точки, двух точек или любого конечного набора точек, очевидно, компактное. Пусть diam Лемма (о вложенности сегментах). Пусть Доказательство. Пусть Б1. 39.Теорема Арцела Теорема (Арцела). Пусть функции заданы fn: K1 → K2 и 1) K1, K2 — компактные метрические пространства; 2) последовательность функций {fn} является равностепенно непрерывной: ∀ε > 0 ∃δ > 0 ∀x, x’ ∈ K1, ∀n ∈ N (ρ1(x, x’)) Тогда из последовательности {fn} можно извлечь подпоследовательность, равномерно сходящуюся к некоторой функции f ∈ C(K1, K2).
Доказательство. 1. Построим (это возможно в силу компактности K1) конечные 1-, 1/ 2 -, 1 /4 и т. д. сети. Упорядочив совокупность точек этих сетей в порядке перечисления и выбрасывая из последовательности повторяющиеся точки, получим счётное всюду плотное в K1 множество X = {x1, x2, x3,..., xl,...}. Для каждого фиксированного l рассмотрим последовательности {fn(xl)}. В силу компактности множества значений K2 с помощью «диагональной процедуры» можно выделить такую подпоследовательность {fnk }, которая будет сходиться в каждой точке xl ∈ X:
Для сокращения записи будем далее обозначать полученную подпоследовательность функций {fnk } одним индексом: fk ≡ fnk, не смешивая её с исходной последовательностью. 2. Докажем, что полученная функциональная подпоследовательность сходится поточечно при всех x ∈ K1, а не только при xl ∈ X, и, более того, сходимость равномерна на K1. Пусть задано ε > 0. Пользуясь неравенством треугольника, запишем для произвольного x ∈ K1:
где xl будет определено ниже. Пользуясь равностепенной непрерывностью исходной функциональной последовательности (а значит, и выбранной подпоследовательности), найдём такое δ > 0, что для всех k ∈ N и ρ1(x’, x”) < δ будет выполнено ρ2(f(x’), f(x”)) < ε /3. Найдём первое среди чисел 2 −j, j ∈ N, меньшее δ. Рассмотрим конечное множество Xj ⊂ X, состоящее из всех элементов выбранных ранее 1-, 1/ 2 -,..., 1/ 2 j - сетей в K1. (Легко видеть, что тогда для каждого x ∈ X ближайший к нему элемент xl ∈ Xj находится на расстоянии меньше δ.) В силу сходимости последовательности {fk} во всех точках Xj (поскольку она по построению сходится всюду на X) существует такое N ∈ N (зависящее только от ε, но не от x!), что для любых k, m > N и для любого xl ∈ Xj верно неравенство ρ2(fk(xl), fm(xl)) < ε/ 3.(3) Поскольку ближайший к произвольному фиксированному элементу x ∈ K1 элемент xl ∈ Xj находится на расстоянии ближе δ, то с учётом выбора δ и два остальных слагаемых в (2) меньше ε /3, откуда мы получаем ρ2(fk(x), fm(x)) < ε. (4) при всех x ∈ K1 и всех k, m > N(ε). Тем самым установлена «равномерная фундаментальность» последовательности {fk} на K1. Из этого факта следует сходимость в каждой точке, а также равномерность этой сходимости: для доказательства последней достаточно перейти в (4) к пределу при m → ∞ (уже зная, что он существует поточечно). Итак, мы доказали, что из данной последовательности можно извлечь равномерно сходящуюся последовательность, предел которой — как равномерный предел непрерывных функций — сам представляет собой непрерывную функцию.
Теорема доказана. Б1. 1. Множество. Подмножество. Равные множества. Пустое множество. Объединение, пересечение, разность, симметрическая разность множеств. Дизъюктные множества.
Б1. 2. Сравнение множеств. Мощность. Примеры.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.33.107 (0.072 с.) |
























 x 0, если
x 0, если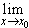
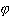 (x) = 1.
(x) = 1.
 X, то, как известно, из существования предела
X, то, как известно, из существования предела  U и x 0
U и x 0  X, то условие (9.24) можно записать в виде
X, то условие (9.24) можно записать в виде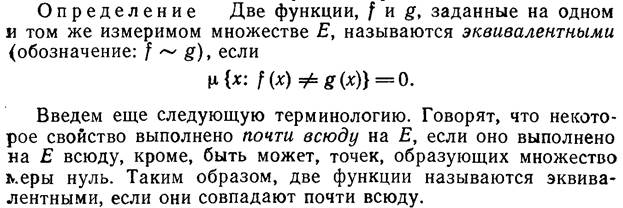





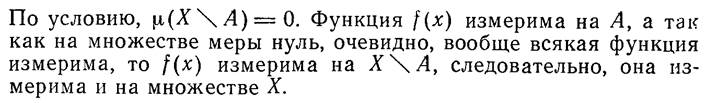






 (Х, τ), если любая ее окрестность имеет непустое пересечение с А.
(Х, τ), если любая ее окрестность имеет непустое пересечение с А. . Число
. Число  называется предельной точкой множества X, если
называется предельной точкой множества X, если

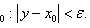





 называется предельной точкой множества
называется предельной точкой множества  , если из этого множества можно выделить последовательность (xn) различных точек, сходящуюся к x 0. (Данное определение и определение, указанное в самом начале эквивалентны)
, если из этого множества можно выделить последовательность (xn) различных точек, сходящуюся к x 0. (Данное определение и определение, указанное в самом начале эквивалентны)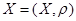 можно вложить в полное метрическое пространство
можно вложить в полное метрическое пространство 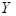 таким образом, что метрика – продолжает метрику Х, а подпространство Х всюду плотно в
таким образом, что метрика – продолжает метрику Х, а подпространство Х всюду плотно в 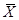 .
.
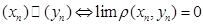
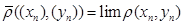 ,
,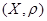 изометрически вкладывается в него следующим образом: точке
изометрически вкладывается в него следующим образом: точке  соответствует класс постоянной последовательности
соответствует класс постоянной последовательности  . Получившееся пространство
. Получившееся пространство 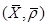 и будет пополнением
и будет пополнением 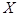 компактно тогда и только тогда, когда оно полно и вполне ограничено, то есть для любого
компактно тогда и только тогда, когда оно полно и вполне ограничено, то есть для любого 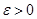 пространство
пространство 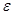
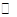 полно в стандартной метрике
полно в стандартной метрике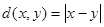
 . Семейство открытых множеств
. Семейство открытых множеств 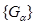 называется открытым покрытием множества Е, если каждая точка
называется открытым покрытием множества Е, если каждая точка  принадлежит хотя бы одному из множеств
принадлежит хотя бы одному из множеств 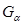 , т.е. если
, т.е. если 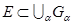 .
. , т.е. верхняя грань расстояний между всевозможными парами точек из Е. Например, если
, т.е. верхняя грань расстояний между всевозможными парами точек из Е. Например, если 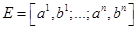 -
- 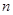 - мерный сегмент, то, diam
- мерный сегмент, то, diam  ,где
,где 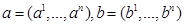 .
.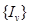 - последовательность вложенных сегментов из
- последовательность вложенных сегментов из  , т.е.
, т.е. 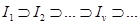 , диаметры которых стремится к нулю при
, диаметры которых стремится к нулю при 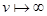 . Тогда существует, и притом единственная, точка
. Тогда существует, и притом единственная, точка 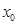 , принадлежащая всем этим сегментам.
, принадлежащая всем этим сегментам.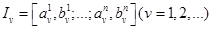 .При каждом фиксированном
.При каждом фиксированном  последовательность одномерных отрезков
последовательность одномерных отрезков  состоит из вложенных друг в друга отрезков, т.е.
состоит из вложенных друг в друга отрезков, т.е. 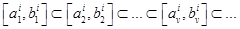 б и длины этих отрезков стремятся к нулю при
б и длины этих отрезков стремятся к нулю при 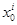 такое, что
такое, что 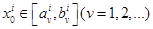 , т.е.
, т.е.  .Но тогда точка
.Но тогда точка 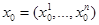 , очевидно, принадлежит всем
, очевидно, принадлежит всем 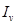 . Двух различных точек, принадлежащих всем
. Двух различных точек, принадлежащих всем 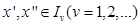 , то
, то 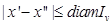 . По условию правая часть стремится к нулю при
. По условию правая часть стремится к нулю при 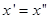
 δ ⇒ ρ2(fn(x), fn(x’))
δ ⇒ ρ2(fn(x), fn(x’))  .(1)
.(1) . (2)
. (2)


