
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приведённая длина физического маятника
Сравним периоды колебаний математического и физического маятников:
Видно, что комбинация параметров физического маятника I/ (ml) имеет размерность длины. Она называется приведённой длиной физического маятника:
Определение 1. Приведённой длиной физического маятника называется длина математического маятника, изохронного данному физическому. Определение 2. Точка О', находящаяся на расстоянии Центр качания О' обладает одним замечательным свойством: если ось качания пропустить через точку О', то период качания ТО' = ТО, т. е. точки О и О' являются изохронными центрами качания. Так например, приведённая длина кольца из Примера 1 l пр = 2 R; приведённая длина стержня из Примера 2 l пр = (2/3) а. 9.7. Преобразования энергии при колебаниях При механических колебаниях происходят периодические преобразования энергии системы из потенциальной в кинетическую и обратно. Рассмотрим такие преобразования на примере пружинного маятника. При максимальном отклонении груза от равновесия его скорость υ = 0, следовательно, его кинетическая энергия W к = 0, но пружина при этом запасла максимальную потенциальную (упругую) энергию W п max = kХ 2 / 2, где k – жёсткость пружины, Х – амплитуда колебаний груза. При возвращении груза к положению равновесия он приобретает максимальную скорость υ0 , значит его кинетическая энергия становится максимальной: W к max = m υ02 / 2, но зато упругая энергия пружины W п = 0. Далее груз, двигаясь по инерции, сжимает пружину, вновь увеличивая её потенциальную энергию и уменьшая свою кинетическую, так как его скорость в процессе сжатия уменьшается. Покажем, что в любой момент времени полная энергия пружинного маятника W полн(t) = W п(t) + W к(t) = const и равна первоначально сообщённой ему энергии W 0 = kХ 2 / 2. Пусть шарику дали начальное отклонение Х и отпустили. Он будет двигаться по закону (9.6). В произвольный момент времени потенциальная энергия пружины
а кинетическая энергия шарика, с учётом (9.7),
Следовательно, полная энергия системы
W полн(t) = W п(t) + W к(t) = Преобразования энергии колебаний математического и физического маятников аналогичны.
Затухающие колебания Во всякой реальной механической колебательной системе имеются силы трения, приводящие к потерям энергии при и колебаниях и уменьшающие их амплитуду. Например, при качаниях груза на пружине или на нити он испытывает трение о воздух. С достаточной точностью силу такого трения можно считать пропорциональной скорости груза (закон Стокса): F тр = − r υ, где r – коэффициент пропорциональности, называемый сопротивлением среды. Знак «−» означает, что F тр ↑↓ υ. Если колебания происходят вдоль оси х, то F тр. х = − r υ х = −r Рассмотрим процесс свободных затухающих колебаний на примере груза на пружине (разд. 9.3). При наличии трения, второй закон Ньютона для такого груза будет иметь вид: m или: m или:
Последнее уравнение удобно записывать в каноническом виде:
где величина
Вид решения уравнения (9.10), как и в разд. 9.3, зависит от способа возбуждения колебаний. Если колебания начинаются при начальном отклонении груза от равновесия на расстояние Х 0 и отпускании его, а сопротивление среды не слишком велико: β < ω0, то решение уравнения (9.10) будет таким: x (t) = X 0 е−β t cos ω t, (9.11) где ω = − угловая частота затухающих колебаний. Видно, что частота колебаний с трением меньше частоты ω0 соответствующих колебаний без трения. Функция (9.11) описывает процесс затухающих колебаний. Её график показан на рис. 9.8.
1. Период. Период колебаний
2. Амплитуда. Экспоненциально убывающий множитель
стоящий в (9.11) перед периодической функцией, называется амплитудой затухающих колебаний (рис. 9.8). 3. Время релаксации. Время τ, за которое амплитуда убывает в е = 2,72 раза, называется временем релаксации, или постоянной времени затухающих колебаний. В соответствии с этим определением,
4. Логарифмический декремент затухания. Натуральный логарифм отношения двух «соседних амплитуд», (т. е. амплитуд, взятых через период Т) называется логарифмическим декрементом затухания δ:
В соответствии с этим определением,
На основе этого определения несложно показать, что если измерить некоторую амплитуду Хk и следующую за ней через N периодов Хk+N, то логарифмический декремент затухания можно определить по формуле
(доказать это самостоятельно). 5. Слабое затухание. Затухание называется слабым, если не просто β < ω0, а β≪ω0. Символ «≪» означает, что меньше, по крайней мере, на порядок. Из соотношения (9.12) следует, что при слабом затухании ω ≈ ω0, т. е. частота свободных колебаний ω практически равна собственной ω0 = 6. Добротность. Важной характеристикой колебательного контура является его добротность Q. Добротность можно определить несколькими эквивалентными способами. Наиболее простое определение такое: Q = т. е. это величина, обратная логарифмическому декременту затухания с множителем π. Добротность является полезной характеристикой контура лишь при слабом затухании; в этом случае
Измерив убывание амплитуды за несколько десятков периодов колебаний даже простого шарика, подвешенного на тонкой нити и качающегося в воздухе, по формуле (9.15) легко подсчитать, что для него величина δ составляет порядка 0,01, следовательно, добротность Q такого маятника составляетпорядка нескольких сотен. 7. Критическое сопротивление среды. Если сопротивление среды достаточно велико, т. е. она «слишком вязкая», то колебаний груза вообще не будет. Например, если груз находится в вязкой жидкости, то при начальном отклонении он затем просто плавно вернётся к равновесию и остановится. Можно показать, что такой процесс плавного возвращения к равновесию без колебаний будет при условии: β ≥ ω0, т. е., в случае пружинного маятника, когда сопротивление среды r ≥ 2
при которой колебательный процесс вырождается в апериодический, называется критическим сопротивлением среды. Можно показать, что в критическом режиме колебательная функция (9.11) вырождается в апериодическую:
График этой функции показан на рис. 9.9. При затухающих колебаниях энергия, периодически превращаясь их потенциальной в кинетическую и обратно, при этом «потихоньку» теряется, рассеиваясь в тепло в основном через трение груза о среду. В качестве полной энергии, имеющейся в колебательной системе в данный момент времени, удобно принять максимум потенциальной энергии, когда кинетическая равна нулю: W полн (t) = kX 2(t) / 2.Подставляя в это выражение формулу (9.13), получаем закон убывания энергии системы при затухающих колебаниях: W полн (t) = W 0 e−2β t , где W 0 − первоначально сообщённая системе энергия. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
|
||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 712; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.208.72 (0.011 с.) |
 ;
;  .
.
 . Тогда можно записать:
. Тогда можно записать:  . Если теперь выбрать длину математического маятника l м = l пр , то он будет изохронным данному физическому, т. е. Т м = Т ф.
. Если теперь выбрать длину математического маятника l м = l пр , то он будет изохронным данному физическому, т. е. Т м = Т ф.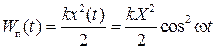 ,
, .
. .
. .
.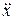 = ∑ Fx = F тр. х + F упр. х = − r
= ∑ Fx = F тр. х + F упр. х = − r  .
. , (9.10)
, (9.10)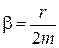 называется коэффициентом затухания, а величина
называется коэффициентом затухания, а величина − собственной частотой колебательной системы. Собственная частота ω0 равна частоте свободных колебаний без трения, но немного отличается от частоты ω свободных колебаний с трением.
− собственной частотой колебательной системы. Собственная частота ω0 равна частоте свободных колебаний без трения, но немного отличается от частоты ω свободных колебаний с трением. (9.12)
(9.12) Для описания затухающих колебаний вводятся следующие понятия и параметры:
Для описания затухающих колебаний вводятся следующие понятия и параметры: .
. , (9.13)
, (9.13)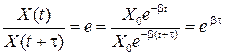 , отсюда
, отсюда  .
.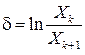 .
. . (9.14)
. (9.14) (9.15)
(9.15) . Кроме того, как следует из (9.14), при слабом затухании
. Кроме того, как следует из (9.14), при слабом затухании  .
.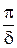 ,
, .
. . Величина
. Величина r = 2
r = 2  .
.


