
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон сохранения импульса системы частиц
Определение. Импульсом системы частиц называется векторная сумма импульсов отдельных частиц: р = ∑ р i. Поскольку при взаимодействии каждой пары частиц внутри системы силы взаимодействия равны и противоположны по направлению, то эти внутренние силы не могут изменить импульса системы. Импульс системы может измениться только под действие какой-то внешней силы F, причём, как и для одной частицы, скорость изменения импульса системы равна этой внешней силе (или векторной сумме всех внешних сил):
Определение. Система частиц называется изолированной, если на неё не действуют никакие внешние силы, т. е. F = 0. В этом случае импульс системы не меняется: р = const. Это утверждение носит название закона сохранения импульса системы частиц. Закон сохранения механической энергии системы частиц Если в изолированной системе действуют только консервативные силы, т. е. нет, например, трения, приводящего к тепловым потерям, то полная механическая энергия этой системы остаётся постоянной: Е = ∑(Ti + Ui) = const (без доказательства). Это утверждение носит название закона сохранения энергии системы частиц.
Столкновение двух тел (удар) При столкновении двух тел (ударе) они испытывают деформацию, и их кинетическая энергия частично или полностью переходит в энергию их упругой деформации, а также рассеивается в виде тепла и уносится звуком. Упругая энергия приводит к отскоку тел, т. е. вновь превращается в их кинетическую энергию, тепловая же и звуковая энергии, выражаемые в нагревании тел, необратимы. Различают два основных типа ударов: абсолютно неупругий и абсолютно упругий. Абсолютно неупругий удар
m 1 υ 1 + m 2 υ 2 = (m 1 + m 2) u, где m 1 и m 2 – массы тел, υ 1 и υ 2 − их скорости до удара, u – их общая скорость после удара (рис. 5.1). Отсюда u = Если векторы υ 1 и υ 2 лежат на одной оси (оси х), то в (5.1) следует подставлять только х -компоненты всех скоростей (с учётом их знаков, разумеется).
Замечание. После удара единое тело может ещё и вращаться, так что следовало бы добавить и закон сохранения момента импульса, позволяющий определить скорость вращения, но этот вариант рассматривать не будем. Пример. Два шарика летят навстречу друг другу по оси х и происходит их прямой удар. Массы шариков m 1 = 1 кг, m 2 = 2 кг, их скорости υ1 = 1 м/с (вправо), υ2 = 2 м/с (влево). Найти их единую скорость шаров ux после их абсолютно неупругого удара. Решение. Для х -компонент скоростей: u = Абсолютно упругий удар Это такой удар, при котором кинетическая энергия сталкивающихся тел частично или полностью (т. е. без тепловых потерь) переходит в энергию их упругой деформации, а затем вновь возвращается в кинетическую энергию разлетающихся тел. При этом оба тела полностью восстанавливают свою форму. При абсолютно упругом ударе выполняются законы сохранения как импульса, так и механической энергии. Определить скорости тел после абсолютно упругого удара значительно сложнее, чем после абсолютно неупругого. Направления и скорости разлёта зависят от конкретной формы тал и от их взаимной ориентации при ударе. Кроме того, в результате удара они могут вращаться. Рассмотрим подробно простейший вариант абсолютно упругого удара – прямой удар двух шаров. Удар называется прямым, если векторы их начальных скоростей υ 1 и υ 2 лежат на линии их центров. В противном случае удар называется косым (рис. 5.2). При косом ударе шары разлетаются под углом к исходным векторам υ 1 и υ 2. При прямом ударе шаров процесс происходит вдоль оси, соединяющей их центры (оси х), поэтому закон сохранения импульса можно записать в алгебраическом виде, т. е. только для х -компонент всех скоростей.
Итак, запишем законы сохранения импульса (для х -компонент) и энергии при прямом абсолютно упругом ударе двух шаров:
где υ1 и υ2 – х- компоненты скоростей шаров до удара, u 1 и u 2 – соответственно после удара, m 1 и m 2 – массы шаров. Пусть скорости υ1 и υ2, а также массы шаров – известны. Определим скорости u 1 и u 2 после удара. Для этого надо решить систему (5.2). Перегруппируем уравнения этой системы:
Разделим второе уравнение этой системы на первое и результат запишем совместно с первым:
Получилась система двух уравнений первой степени. Её решение имеет вид: u 1 = При m 1 = m 2 , то u 1 = υ2, u 2= υ1, т. е. шары обмениваются скоростями. Если m 1 = 1 кг, υ1 = 1 м/с, m 2 = 2 кг, υ2 = –2 м/с, то скорости разлёта шаров будут такими: u 1 = – 3 м/с; u 2 = 0, т. е. первый шар полетит назад со скоростью 3 м/с, а второй шар после удара остановится. Центр масс В любой системе частиц есть особая точка С, называемая центром масс. Её положение в выбранной системе координат определяется вектором
где mi и r i − масса и радиус-вектор i -той частицы, Векторное определение (5.3) эквивалентно трём скалярным, определяющим декартовы координаты центра масс:
Комментарий. Выражение Пример 1. Найти центр масс системы двух частиц массами m 1 = 1 кг и m 2 = 1 кг, на расстоянии l = 1 м друг от друга. Решение. Положим частицы на ось х, и пусть х 1 = 0, х 2 = l = 1 м. Тогда
Для нахождения центра масс сплошного тела его надо разбить на малые частицы (например, кубики) массой dm = ρ dV, где ρ – плотность тела, dV – элементарный объём кубика. И пусть r – радиус-вектор этого кубика. Тогда правая часть (5.3) становится предельной суммой, т. е. интегралом по всему объёму V тела:
Векторное соотношение (5.4), как и (5.3), эквивалентно трём скалярным. Ясно. что центр масс всякого тела должен находиться где-то внутри выпуклого многогранника, охватывающего тело. Но вовсе не обязательно, чтобы он лежал в самŏм теле. Например, центры масс кольца и полукольца лежат вне этих тел. Пример 2. Найти центр масс полушара радиусом R. Решение. Очевидно, что центр масс полушара должен лежать где-то на его оси. Обозначим её осью х, положив х = 0 в центре основания полушара. Тогда, в соответствии с (5.4), получаем, что координата центра масс
Если нам удастся выразить элемент объёма dV как функцию х, то объёмный интеграл сведётся к обыкновенному. Для этого разобъём полушар на тонкие диски толщиной dx (рис. 5.4). На высоте х радиус такого диска r = dV = π r 2 dx = π(R 2 – x 2) dx. Тогда, учитывая, что объём полушара V = (2/3)π R 3, получаем:
|
||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 1062; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.36.10 (0.017 с.) |
 ∑ F внеш.≡ F.
∑ F внеш.≡ F. Это такой удар, после которого оба тела движутся как единое целое. При этом упругой деформации не возникает или же она очень мала и не приводит к отскоку, а кинетическая энергия тел частично или полностью превращается в тепловую. Поэтому при абсолютно неупругом ударе закон сохранения механической энергии не выполняется, а выполняется только закон сохранения импульса:
Это такой удар, после которого оба тела движутся как единое целое. При этом упругой деформации не возникает или же она очень мала и не приводит к отскоку, а кинетическая энергия тел частично или полностью превращается в тепловую. Поэтому при абсолютно неупругом ударе закон сохранения механической энергии не выполняется, а выполняется только закон сохранения импульса: . (5.1)
. (5.1) = −1 м/с.
= −1 м/с.
 (5.2)
(5.2)

 , u 2 =
, u 2 =  .
.
 , (5.3)
, (5.3) − масса всей системы (рис. 5.3).
− масса всей системы (рис. 5.3).
 означает, что хС − это некоторое среднее х- координат всех частиц с весовыми множителями m i. Если все массы mi одинаковы, то хС − это просто среднее арифметическое х- координат всех частиц:
означает, что хС − это некоторое среднее х- координат всех частиц с весовыми множителями m i. Если все массы mi одинаковы, то хС − это просто среднее арифметическое х- координат всех частиц: 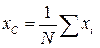 , где N – количество частиц в системе.
, где N – количество частиц в системе. м.
м. . (5.4)
. (5.4)
 .
. , а его объём
, а его объём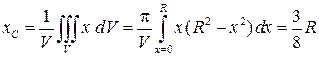 .
.


