Силовое поле. Работа и энергия

Силовое поле

Допустим, частица массой m находится в области притяжения какой-то звезды массой М. По закону всемирного тяготения, со стороны этой звезды на частицу действует сила F, направленная к центру звезды:

,

где G – гравитационная постоянная, r – расстояние от частицы до звезды. Если помещать частицу то в одну, то в другую точку пространства (х, у, z), то в каждой точке на частицу будет действовать сила F вполне определённой величины и направления: F = F (х, у, z) (рис. 4.1). В этом случае говорят, что частица находится в силовом поле F (х, у, z). Природа силы F может быть любой: гравитационная, кулоновская, магнитная, упругая.

Теперь сформулируем общее определение силового поля: если в каждой точке (х, у, z) пространства определена сила F = F (х, у, z), действующая на частицу в этой точке и зависящая от координат этой точки, то говорят, что задано силовое поле F (х, у, z).

Для наглядности силовое поле принято изображать силовыми линиями. Силовая линия – это ориентированная линия в пространстве, касательная в каждой точке которой показывает направление силы, действующей на частицу, помещённую в эту точку. Плотность силовых линий пропорциональна величине силы. Так например, силовые линии гравитационного поля точечной или шаровой массы – это радиальные лучи, направленные из бесконечности к этой массе (рис. 4.2, а).

Частным вариантом силовых полей является однородное поле – это поле, постоянное по величине и направлению F = const. Его силовые линии – параллельные равноудалённые ориентированные прямые (рис. 4.2, б). Однородное поле – это идеализация. Однако, всякое радиальное поле в небольших объёмах можно считать примерно однородным. Например, поле Земли на площади в несколько квадратных километров и до высот 50-100 км вполне можно считать однородным: F ≈ const↑↑g, где | g| = 9,8 м/c² – ускорение свободного падения у поверхности Земли.

Работа поля

Пусть частица в силовом поле F (х, у, z) перемещается вдоль некоторой ориентированной кривой 1−2. Разобъём эту кривую на малые участки Δl _k, которые можно считать малыми векторами (рис. 4.3). На каждом участке на частицу действует сила F _k.

Определение 1. Скалярное произведение вектора F _k на Δl _k называется элементарной работой Δ А_k поля F (силы F) на участке Δl _k:

Δ А_k = F _k ·Δl _k = F_k cos α _k Δ l_k,

где α _k – угол между векторами F _k и Δl _k.

Определение 2. Предельная сумма всех элементарных работ Δ А_k на участке кривой 1−2 (криволинейный интеграл) называется работой поля F на этом участке:

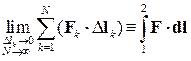А = . (4.1)

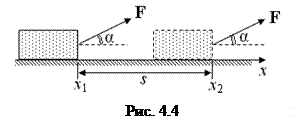Пример 1. Пусть под действием постоянной силы F тело перемещается по оси х от точки х ₁ до х ₂ на расстояние s = х ₂ − х ₁ (рис. 4.4). Тогда, по определению, работа этой силы

А = = F (х ₂ − х ₁) cos α = Fs cos α.