
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь работы потенциального поля с изменением энергии
Введём базовую точку М 0. Тогда, используя свойство аддитивности работы и независимость работы от формы пути, получаем: А 1−2 = Но, по определению,
следовательно, А 1-2 = U 1 − U 2 = −Δ U. (4.4) Таким образом, работа потенциального поля между двумя точками равна убыли потенциальной энергии частицы: если работа поля А 1-2 > 0, то потенциальная энергия частицы уменьшается, а при А 1-2 < 0 увеличивается. Замечание. Δ U = U 2 − U 1 − это приращение энергии, а U 1 − U 2 − убыль. Потенциальная энергия в системе СИ, как и работа, измеряется в джоулях. Кинетическая энергия Пусть на частицу действует сила F любой природы. Это означает, что: 1) скорость частицы меняется в соответствии с законом Ньютона: F = m 2) сила F совершает работу. Элементарная работа силы F: dA = F·dl = m Видно, что работа силы F идёт на приращение некоторой величины в скобках. Эта величина носит название кинетической энергии Т частицы: Т = При элементарной работе силы F любой природы приращение кинетической энергии частицы dT = dA, а при конечном перемещении частицы изменение её кинетической энергии Δ Т = Т 2 − Т 1 = А 1-2 . (4.5) Если А 1-2 > 0, то кинетическая энергия возрастает, а при А 1-2 < 0 − убывает. В системе СИ кинетическая энергия, как и работа, измеряется в джоулях. Полная механическая энергия Работу может совершать сила любой природы − как сила F конс. со стороны самогǒ потенциального поля (она называется консервативной), так и сила любой иной природы F стор. (такие силы называются сторонними), или же их комбинация. Например. частица может двигаться в потенциальном поле тяжести, но с трением, т. е. F = F конс. + F тр . В гравитационном поле сторонними силами могут быть силы трения, упругости. Таким образом, в общем случае: F = F конс. + F стор.. Тогда выражение (4.5) можно представить в виде: Δ Т = А конс. + А стор., где А конс. = Δ Т = −Δ U + А стор., или: Δ(T + U) = А стор. . (4.6)
Отсюда видно, что работа поля сторонних сил идёт на приращение некоторой величины (T + U). Эта величина − сумма кинетической и потенциальной энергий − называется полной механической энергией частицы в потенциальном поле и обозначается символом Е: Е = Т + U. Таким образом, приращение полной механической энергии частицы равно работе сторонних сил: Δ Е = Е 2 − Е 1 = А стор. . (4.7) Пример. Тело массой m сила F = 2 mg поднимает вверх. Найти скорость тела на высоте h. Решение. Работа силы A = Fh = Δ E = Δ U + Δ T = mgh + m υ2 / 2. Отсюда υ =
|
|||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 334; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.250.114 (0.022 с.) |
 Выберем в пространстве две произвольные точки 1 и 2 и вычислим работу потенциального поля F от точки 1 до 2 (рис. 4.11).
Выберем в пространстве две произвольные точки 1 и 2 и вычислим работу потенциального поля F от точки 1 до 2 (рис. 4.11). .
. ,
,  ,
, ;
;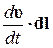 = m (υ· d υ) = m d
= m (υ· d υ) = m d  *).
*). .
. − работа консервативной силы, А стор. =
− работа консервативной силы, А стор. =  − работа сторонней силы. Но, согласно (4.4), работа консервативной силы равна убыли потенциальной энергии частицы: А конс. = −Δ U, следовательно,
− работа сторонней силы. Но, согласно (4.4), работа консервативной силы равна убыли потенциальной энергии частицы: А конс. = −Δ U, следовательно, .
.


