
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства работы. Единица работы
Пример 2. Спутник движется вокруг Земли по круговой орбите под действием силы тяжести F (рис. 4.5). Здесь работа силы тяжести по перемещению спутника равна нулю, так как в любой точке круговой орбиты dl Пример 3. Камень летит вверх в однородном поле тяжести Земли. Здесь сила тяжести F = m g направлена вниз, а вектор перемещения камня − вверх; значит, α = 180º, и работа силы тяжести отрицательна. Свойство 2: работа А является величиной аддитивной. Это значит. что если всю траекторию частицы разбить на отдельные участки, то общая работа на траектории равна алгебраической сумме работ на участках: А = ∑ Аk. Свойство 3. При смене направления интегрирования работа меняет знак:
Это следует из того, что при смене ориентации элемента dl скалярное произведение F ·dl в каждом слагаемом предельной суммы (4.1) меняет знак. В системе СИ работа измеряется в джоулях: 1 Дж = (F= 1 Н) · (l = 1 м). Мощность Одна и та же работа может быть совершена за разное время. Для характеристики скорости совершения данной работы вводится понятие мощности. Определение. Пусть сила F совершила работу А за время Δ t. Тогда величина Р = А/ Δ t называется мощностью, развиваемой силой F на данном интервале времени. Так как работа А = F· Δ l, то мощность можно представить в виде: Р = F·υ, где υ − скорость тела в данный момент. В системе СИ мощность измеряется в ваттах: 1 Вт = Потенциальное поле
А 1−2 = В общем случае работа (4.2) зависит от формы кривой 1-2, т. е. по разным траекториям она будет разной: А 1-2(I) ≠ А 1-2(II) (рис. 4.6). Однако, существуют силовые поля, в которых работа (4.2) не зависит от формы пути, а определяется только положениями исходной и конечной точек. Такие поля называются потенциальными.
А 1−2 = Но: dl cos α = − dr,
А 1−2 = GMm Отсюда видно, что работа поля F не зависит от формы пути 1−2, а определяется только координатами точек 1 и 2, а именно только от их расстояний r 1 и r 2 до центра звезды М. Следовательно, гравитационное поле F (х, у, z) является потенциальным. Несложно показать, что однородное поле также является потенциальным. Следствие. Работа потенциального поля по любой замкнутой траектории (т. е. по контуру) равна нулю. Доказательство. Рассмотрим рис. 4.6. Две траектории на нём I и II образуют замкнутую кривую. По определению потенциального поля, работы по этим траекториям от точки 1 до 2 одинаковы: А 1-2(I) = А 1-2(II). А так как при смене направления интегрирования работа меняет знак, то А 2-1(II)= − А 1-2(II). Следовательно, А 1-2(I) + А 2-1(II) = 0. А это и есть работа по замкнутой траектории, т. е. по контуру.
|
|||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 358; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.81.240 (0.006 с.) |
 Свойство 1: работа А есть величина скалярная и алгебраическая, т. е. она может быть положительной, отрицательной и нулевой, в зависимости от угла α между силой и перемещением.
Свойство 1: работа А есть величина скалярная и алгебраическая, т. е. она может быть положительной, отрицательной и нулевой, в зависимости от угла α между силой и перемещением. F.
F. .
. .
. Итак, если в силовом поле F (х, у, z) частица перемещается из точки 1 в 2, то это поле совершает работу
Итак, если в силовом поле F (х, у, z) частица перемещается из точки 1 в 2, то это поле совершает работу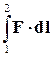 . (4.2)
. (4.2) Покажем, что гравитационное поле точечной (или шаровой) массы М является потенциальным. Для этого вычислим работу такого поля от точки 1 до 2 по произвольной кривой 1-2 (рис.4.7):
Покажем, что гравитационное поле точечной (или шаровой) массы М является потенциальным. Для этого вычислим работу такого поля от точки 1 до 2 по произвольной кривой 1-2 (рис.4.7):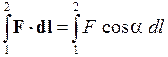 .
. . Следовательно,
. Следовательно,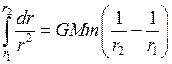 .
.


